终于要开始学习&&复习这个知识点了，说句实话半年多之前就该写这篇文章来加强理解，但是一直没有落实，因为又去练习了很多学过的算法，感觉这个算法不太常用哦，传说中的省选算法，比赛比较少见（可能是开不到吧。。。），想把这些东西和思维融为一体确实不容易，那么这就开始吧

简介

• 如下图，$s$是起点，$t$是终点，其中边权表示每条管道中水的最大流量$(capacity)$，问从$s$到$t$一次最多能送多少水
• 我们还要介绍另外两个概念，残留量$(residual)$，也就是空闲量，即当前管道里面还能加入多少水，因为开始的时候管道里面水量是$0$，所以一开始管道的空闲量为最大流量；流量$flow$，也就是管道里面实际有多少的水，所以对于每条管道，有$flow=capacity-residual$
• 我们想一下怎么解决这个问题，或许我们会想到一种办法，寻找一条从$s$到$t$的路径，那么这条路径上面边权最小的那条边权就是路径的瓶颈，也就是这条路径的$flow$，这个想法是对的，但是我们接下来怎么办呢，如果再以类似的方法去找另外的路径这样得到的结果不一定是最优，所以引入了反向路径这个概念来解决这个问题

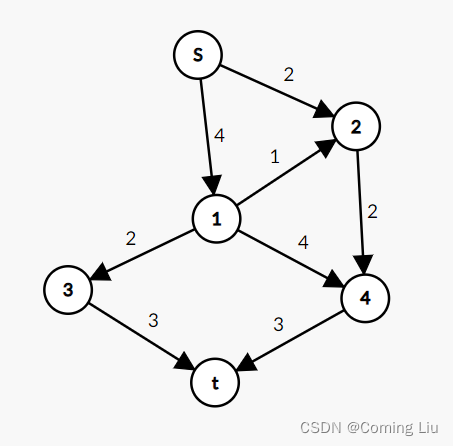
Ford-Fulkerson

• $FF$方法的思路和前面提到的想法有些类似，我们从$s$出发，随便找一条能够到达$t$的简单路径，找到路径中的最小值，把整条路经所有边的边权都减去这个值，如果减为$0$，那么视为删除这条边，同时这条路径上的所有边都重新建立一条反向路径，边权和这个最小边权的权值相等，这样就可以起到一个反悔的作用，能够证明这种方法总能够找到最优解
• 上面的这个过程叫做找从$s$到$t$的一个增广路，也就是路径上的边的容量都要$>0$
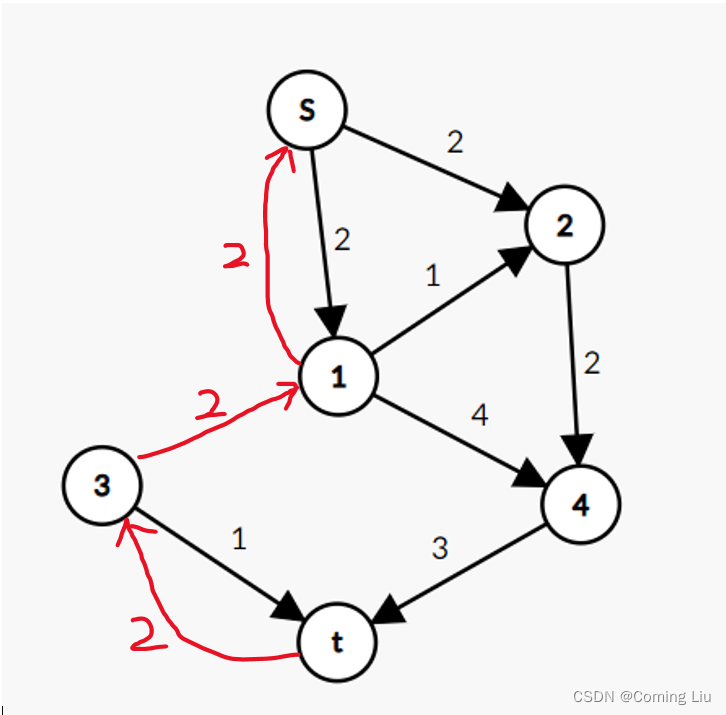
• 比如上面的图我找到了一条从起点到终点的增广路$s\to 1\to 3\to t$，因为这里面最小的容量是$2$，所以接下来的图就会是下面这个样子，红色边表示添加的反向边，这样一直找到再也没有$s$到$t$的简单路径，把每次减去的容量加在一起就是最大流
  
• 这种算法的时间复杂度是$O(f\times m)$，$f$表示最大网络流，$m$表示边数，因为采用$dfs$进行搜索，可能会出现每次搜索只能增加$1$的贡献，导致速度很慢

Edmonds–Karp算法

• $EK$算法是$FF$思想的实现方式，它采用$bfs$而非$dfs$进行搜索，好处是不会陷入某条边的漩涡中，时间复杂度能达到$O(m^{2}n)$，$m$表示边数，$n$表示点数

https://www.luogu.com.cn/problem/P3376

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

int main(){
  ios::sync_with_stdio(false);
  cin.tie(0);
  cout.tie(0);
  int n, m, s, t;
  cin >> n >> m >> s >> t;
  vector<vector<ll> > g(n + 1, vector<ll>(n + 1));
  for(int i=0;i<m;i++){
    int u, v, w;
    cin >> u >> v >> w;
    g[u][v] += w;
  }
  vector<ll> flow(n + 1);
  vector<int> pre(n + 1);
  function<ll(int, int)> Bfs = [&](int s, int t){
    queue<int> q;
    fill(pre.begin(), pre.end(), -1);
    q.push(s);
    int ans = 0;
    flow[s] = LONG_LONG_MAX;
    pre[s] = 0;
    while(!q.empty()){
      int u = q.front();
      q.pop();
      for(int i=1;i<=n;i++){
        if(pre[i] == -1 && g[u][i] != 0 && i != s){
          q.push(i);
          flow[i] = min(flow[u], g[u][i]);
          pre[i] = u;
        }
      }
    }
    if(pre[t] == -1) return -1ll;
    return flow[t];
  };
  function<ll(int, int)> maxFlow = [&](int s, int t){
    ll ans = 0;
    while(1){
      ll flow = Bfs(s, t);
      if(flow == -1ll) break;// 找不到增广路
      int cur = t;
      while(cur != s){
        int fa = pre[cur];
        g[fa][cur] -= flow;
        g[cur][fa] += flow;
        cur = fa;
      }
      ans += flow;
    }
    return ans;
  };
  cout << maxFlow(s, t) << '\n';
  return 0;
}

Dinic

• 这个算法相对于之前的$EK$算法改进点在于它使用了一个$O(n^2)$构造的分层图，所谓分层就是按照它到源点的最短距离分成若干层，然后只能在层间转移而不能在层内转移
• 这种算法的时间复杂度在使用弧优化的前提下是$O(n^{2}m)$的，$Dfs$是$O(m)$，$Bfs$是$O(n^2)$

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int V = 1225;
const int E = 1e5 + 3e4;
struct Edge{
  int nxt;
  int to;
  ll val;
}edge[E << 1];
int cnt = 2;
int head[V];
void Add_Edge(int u, int v, ll w){
  edge[cnt].nxt = head[u];
  edge[cnt].to = v;
  edge[cnt].val = w;
  head[u] = cnt++;
}
int dep[V];
int cur[V];
bool Bfs(int s, int t){
  memset(dep, 0, sizeof dep);
  queue<int> q;
  q.push(s);
  dep[s] = 1;
  while(!q.empty()){
    int u = q.front();
    q.pop();
    for(int i=head[u];i;i=edge[i].nxt){
      int v = edge[i].to;
      if(dep[v] == 0 && edge[i].val > 0){
        dep[v] = dep[u] + 1;
        q.push(v);
        if(v == t) return true;
      }
    }
  }
  return false;
}
ll Dfs(int u, int t, ll mf){
  if(u == t) return mf;
  ll sum = 0;
  for(int i=cur[u];i;i=edge[i].nxt){
    cur[u] = i;// 当前弧优化
    int v = edge[i].to;
    if(dep[v] == dep[u] + 1 && edge[i].val > 0){
      ll f = Dfs(v, t, min(mf, edge[i].val));
      edge[i].val -= f;
      edge[i ^ 1].val += f;// 更新残留网络
      sum += f;
      mf -= f;
      if(mf == 0) break;// 余量为0
    }
  }
  if(sum == 0) dep[u] = 0;// 如果走不到终点, 说明这个点没用了
  return sum;
}
ll Dinic(int s, int t){
  ll flow = 0;
  while(Bfs(s, t)){
    memcpy(cur, head, sizeof head);
    flow += Dfs(s, t, INT_MAX);
  }
  return flow;
}
int main(){
  ios::sync_with_stdio(false);
  cin.tie(0);
  cout.tie(0);
  int n, m, s, t;
  cin >> n >> m >> s >> t;
  for(int i=0;i<m;i++){
    int u, v;
    ll w;
    cin >> u >> v >> w;
    Add_Edge(u, v, w);
    Add_Edge(v, u, 0ll);
  }
  cout << Dinic(s, t);
  return 0;
}

还有一种算法是$ISAP$，复杂度是$O(n{m}^2)$，以后有时间再看吧