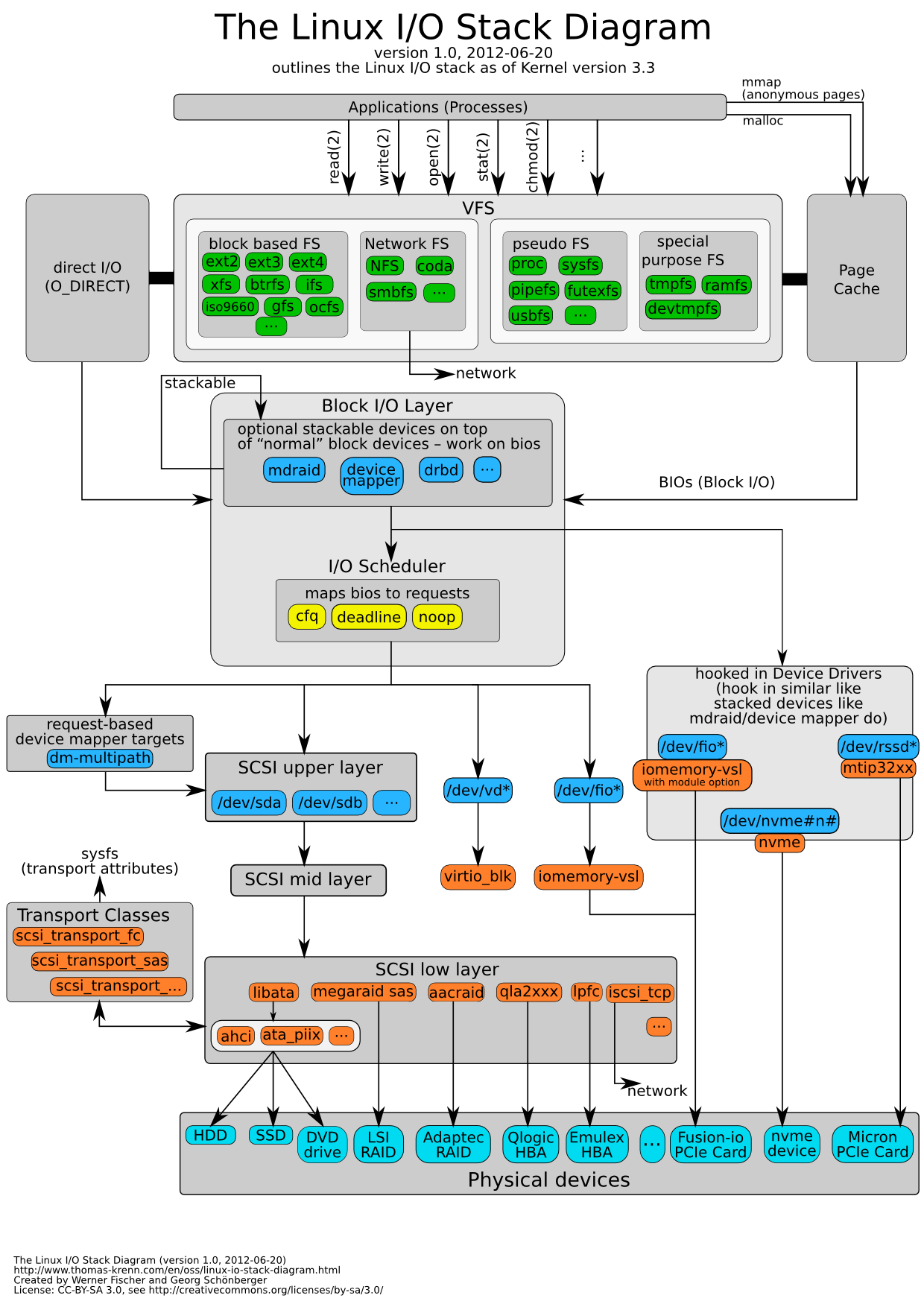
机器学习（二） 线性代数基础I（Linear Algebra Foundations)

这一节主要介绍一些线性代数的基础。

1. 向量 Vectors

一般用向量来表示输入数据的特征。
向量是行表示还是列表需要根据具体的问题确定，在本系列的标记中，没有特殊说明就是列向量，例如a是列向量，则a^T是行向量
向量的运算：
addition: commutative（交换律), associative（结合律）
subtraction
scalar-verctor mutliplication: associative, left distributive, right distributive
inner product, <a,b> 或者a·b

2. 复杂度 Complexity

在这里使用的都看为浮点数运算，基础的数学运算（arithmetic operation），包括addition,subtraction,mutliplication都看作为floating point operations 或者 flops。
探索复杂度则是考虑完成某个运算或者算法需要的全部flops。
我们一般大致估算这些复杂度。

3.线性函数 Linear Function

这里直接把课堂PPT放上来。
在这里插入图片描述

4. 模，范数 Norm

5. RMS

注意到RMS是可以用于对比不同sizes的向量的。

6. 切比雪夫不等式 Chebyshev inequality

NOTE:这里是fraction，是比例，把（rms(x)/a）^2展开之后，里面有一个n,k/n刚好就是比例。

7. 标准差 Standard deviation

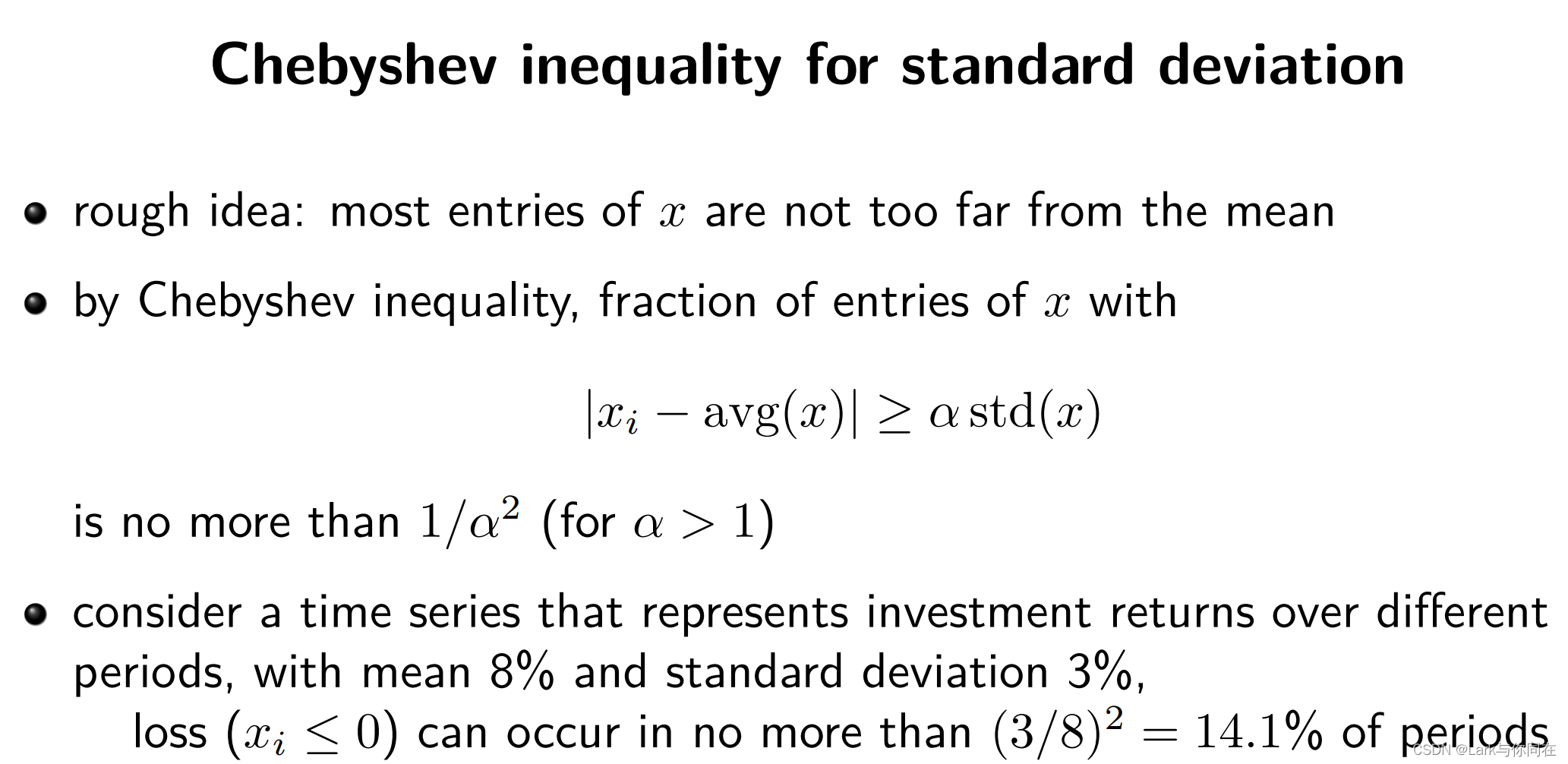
作业实战应用——聚类 Clustering

I 理论分析题-为什么使用均值中点作为代表点

答案：

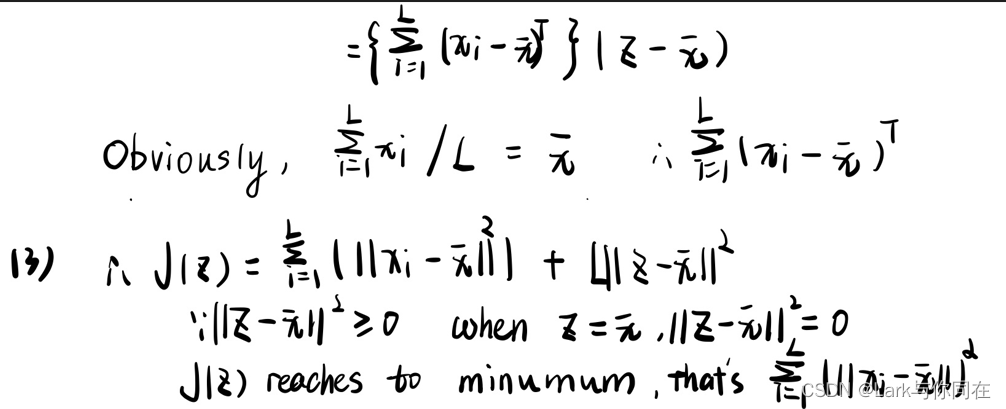
II 理论分析题-线性二分类

答案：

III 代码实践 Iris聚类

3.1 Load the data

#LoadData
#input: path for data
#output: data(array), features(str)
def LoadData(path):
    df = pd.read_csv(path) # df contains the keys as well as the values
    feature_names = df.keys()
    X = df.iloc[:, 0:4].to_numpy()#get all the rows and column 0,1,2,3 four features
    return X,feature_names

3.2 K-means Algorithm

# author: xxx
# University: xxx
# Usage: some wheels for k-means algorithm
# theory:
#Given x1,x2...xn and z1,z2,...zk(data, representatives)
#repeat
    #update partition : assign xi to Gj, make sure ||xi-zj||^2 minimum
    #update representatives
#until z1,z2,...zk remain unchanged  #convert to J unchanged
import numpy as np
from numpy import linalg as la
def k_means(data:'array',K:"int"=3,maxiters:'int'=30,loss:'f32'=0.0001):
    N=data.shape[0]# row of data
    assignment=np.zeros(N)
    initial=np.random.choice(N,K,replace=False)
    reps=data[initial,:]#
    for j in range(K):#update assignment, otherwise some groups number is 0
        assignment[initial[j]]=j
    distance=np.zeros(N)
    Jprev=np.infty
    for iter in range(maxiters):
        for i in range(N):
            ci=np.argmin([la.norm(data[i]-reps[p])for p in range(K)])
            assignment[i]=ci
            distance[i]=la.norm(data[i]-reps[ci])
            for j in range(K):#update reprentatives
                group=[i for i in range(N) if assignment[i]==j]
                SUM=np.sum(data[group],axis=0)
                lenN=len(group)
                #print(lenN)
                reps[j]=SUM/lenN
            J=la.norm(distance)**2/N# **2 means ^2
            if(iter>maxiters) or np.abs(J-Jprev)<(loss)*J:

                break
            Jprev=J
    print("iter:",iter)
    return assignment,reps

3.3 画3Dscatter图

def showfigure(classes,features:"4+1 key",reps):

    feature_names = features
    plt.figure()
    class_N=len(classes)

    ax = plt.axes(projection='3d')
    for i in range(class_N):
        data=classes[i]
        ax.scatter(data[:, 0], data[:, 1], data[:, 2])
    ax.scatter(reps[:,0], reps[:, 1], reps[:, 2],marker='X')
    ax.set_xlabel(feature_names[0])
    ax.set_ylabel(feature_names[1])
    ax.set_zlabel(feature_names[2])
    plt.show()

主函数

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from K_MEANS import *
if __name__ == '__main__':
    path='data/iris.csv'
    class_K=3
    data,features=LoadData(path)
    assignmnet,reps=k_means(data,K=class_K)
    #print(list(enumerate(assignmnet)))
    class_data = []
    class_index=[]
    for j in range(class_K):
        class_index.append([i for i,x in enumerate(assignmnet) if x==j])
        G=np.array(data[class_index[j],:])
        class_data.append(G)
    showfigure(class_data,features,reps)

IV MNIST 数据集聚类

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from K_MEANS import *
plt.ion()
# read MNIST training data
def LoadData(path):
    df = pd.read_csv(path)
    X = df.iloc[:, 1:].to_numpy() / 255.0       # values are scaled to be between 0 and 1
    y = df.iloc[:, 0].to_numpy()                # labels of images
    return X,y
def ShowFigure(X,RepsLabels):
    plt.figure()
    num=X.shape[0]
    print(num)
    row=4
    column=num//row
    for i in range(num):
        ax=plt.subplot(row, column, i + 1, xticks=[], yticks=[])
        image = X[i, :].reshape((28, 28))
        ax.set_title("Repres:%d"%RepsLabels[i],loc='center')
        plt.imshow(image, cmap='gray')
    plt.tight_layout()
    plt.show()
def Classifier(repres,represlabel,testdata,testlabels):
    accuracy=0
    K=repres.shape[0]# K classes
    N=testdata.shape[0] # N test data
    CorrectNum=0
    for i in range(N):
        prediction=np.argmin([la.norm(testdata[i]-repres[p])for p in range(K)])
        if represlabel[prediction]==testlabels[i]:
            #classified successfully
            CorrectNum+=1
    accuracy=CorrectNum/N
    print("accuracy:",accuracy)
    return accuracy

if __name__ == '__main__':
    path='data\mnist_train.csv'
    data, labels = LoadData(path)
    testpath='data\mnist_test.csv'
    testdata, testlabels = LoadData(path)
    class_K = 20
    accuary=[]
    for n in range(10):
        assignmnet, reps, J_List = k_means(data, maxiters=30,K=class_K)
        np.savetxt(f"MNISTAss{n}.cvs",assignmnet,fmt="%d")
        # print(list(enumerate(assignmnet)))
        class_data = []
        class_index = []
        class_labels=[]
        for j in range(class_K):
            class_index.append([i for i, x in enumerate(assignmnet) if x == j])
            G = np.array(data[class_index[j], :])
            Prelabels=np.argmax(np.bincount(labels[class_index[j]]))
            class_labels.append(Prelabels)
            class_data.append(G)
        print(class_labels)
        ShowFigure(reps,class_labels)
        a=Classifier(reps,class_labels,testdata,testlabels)
        accuary.append(a)

    plt.figure()
    print("len(accuary)", len(accuary))
    x_axis_data = [i + 1 for i in range(len(accuary))]  # x
    y_axis_data = [accuary[i] for i in range(len(accuary))]  # y
    print(y_axis_data)
    plt.plot(x_axis_data, y_axis_data, 'b*--', alpha=0.5, linewidth=1,
             label='Classification Accuracy')  # 'bo-'表示蓝色实线，数据点实心原点标注
    ## plot中参数的含义分别是横轴值，纵轴值，线的形状（'s'方块,'o'实心圆点，'*'五角星   ...，颜色，透明度,线的宽度和标签 ，

    plt.legend()  # 显示上面的label
    plt.xlabel('Test Count')  # x_label
    plt.ylabel('Accuracy')  # y_label
    plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))
    #plt.gca().yaxis.set_major_locator(MaxNLocator(integer=True))
    plt.show()
# plot the first dozen images from the data set