题目描述

给定字符串 s 和字符串数组 words, 返回 words[i] 中是s的子序列的单词个数 。

字符串的 子序列 是从原始字符串中生成的新字符串，可以从中删去一些字符(可以是none)，而不改变其余字符的相对顺序。

例如， “ace” 是 “abcde” 的子序列。

示例 1:

输入: s = “abcde”, words = [“a”,“bb”,“acd”,“ace”]
输出: 3
解释: 有三个是 s 的子序列的单词: “a”, “acd”, “ace”。
Example 2:

输入: s = “dsahjpjauf”, words = [“ahjpjau”,“ja”,“ahbwzgqnuk”,“tnmlanowax”]
输出: 2

提示:

1 <= s.length <= 5 * 104
1 <= words.length <= 5000
1 <= words[i].length <= 50
words[i]和 s 都只由小写字母组成。

求解思路

1. 实现思路1:双指针，判断s是否为t的子序列问题，通过双指针来求解，如果位置i它们的字符值相等，指向s的指针i++，指向t的指针j++，如果不相等，那么t的指针j++，最后判断i是否来到了字符串s的位置，如果来到了，返回true，否则返回fasle。
2. 题目数据范围恰到好处，当然不会让你这么容易的就通过，所以我们就演进出了第二种求解思路，就是通过一个容器事先记录好t每一个元素出现的位置，元素可能有多个，我们选择List集合。在遍历的过程中，对于需要匹配的字符 ，我们就可以通过在对应的集合中进行「二分查找」来找到第一个大于当前 i 指针的位置，如果不存在直接匹配失败，如果匹配成功就直接将j指针移动到查找的位置，i指针移动到下一个位置，实现了匹配过程的加速。

实现代码&运行结果

实现代码1:

class Solution {
    public int numMatchingSubseq(String s, String[] words) {
        int cnt=0;
        for(int i=0;i<words.length;i++){
            if(isSubsequence(words[i],s)) cnt++;
        }
        return cnt;
    }


    public boolean isSubsequence(String s, String t) {
        int n = s.length(), m = t.length();
        int i = 0, j = 0;
        while (i < n && j < m) {
            if (s.charAt(i) == t.charAt(j)) {
                i++;
            }
            j++;
        }
        return i == n;
    }

}

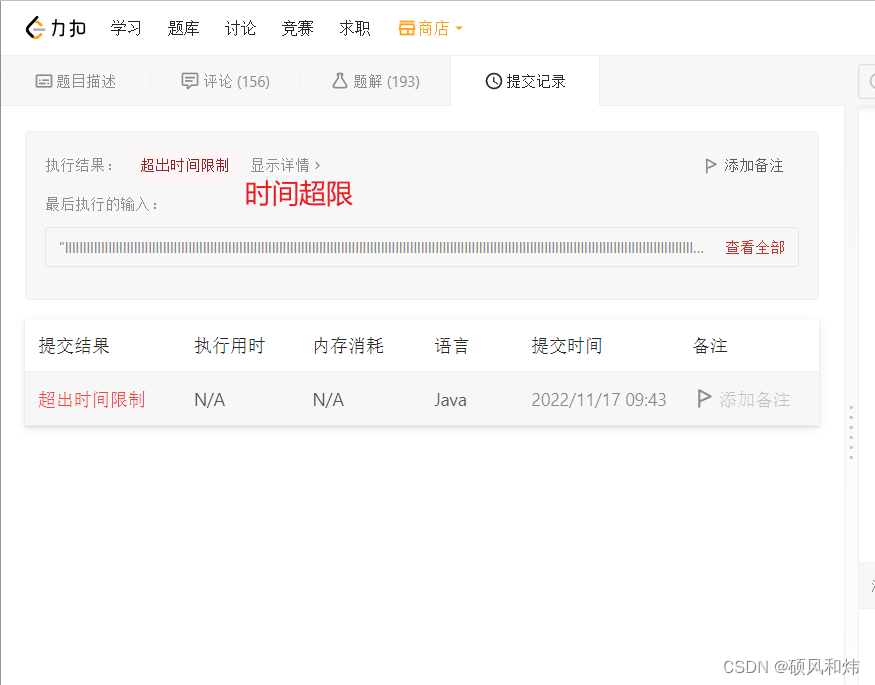
运行结果1：

实现代码2：参考官方实现的代码

class Solution {
    public int numMatchingSubseq(String s, String[] words) {
        List<Integer>[] pos = new List[26];
        for (int i = 0; i < 26; ++i) {
            pos[i] = new ArrayList<Integer>();
        }
        for (int i = 0; i < s.length(); ++i) {
            pos[s.charAt(i) - 'a'].add(i);
        }
        int res = words.length;
        for (String w : words) {
        	//数组中的字符串如果都比s的长度长了，那么肯定就符合题目的要求了，res--
            if (w.length() > s.length()) {
                --res;
                continue;
            }
            //挨个遍历w的长度
            //p就是大于当前i指针的位置
            int p = -1;
            for (int i = 0; i < w.length(); ++i) {
                char c = w.charAt(i);
                //如果当前位置的是元素对应的集合是空---》不符合子序列--》再次减1
                //如果某一个位置的元素它的最后一个元素的下标位置是小于等于我们的p值，不符合题目，减1
                if (pos[c - 'a'].isEmpty() || pos[c - 'a'].get(pos[c - 'a'].size() - 1) <= p) {
                    --res;
                    break;
                }
                //二分查找的值再次给我们的是p，更新p值
                p = binarySearch(pos[c - 'a'], p);
            }
        }
        return res;
    }

	//二分查找---在给定的集合中查找大于当前位置的第一个下标位置
    public int binarySearch(List<Integer> list, int target) {
        int left = 0, right = list.size() - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (list.get(mid) > target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return list.get(left);
    }
}

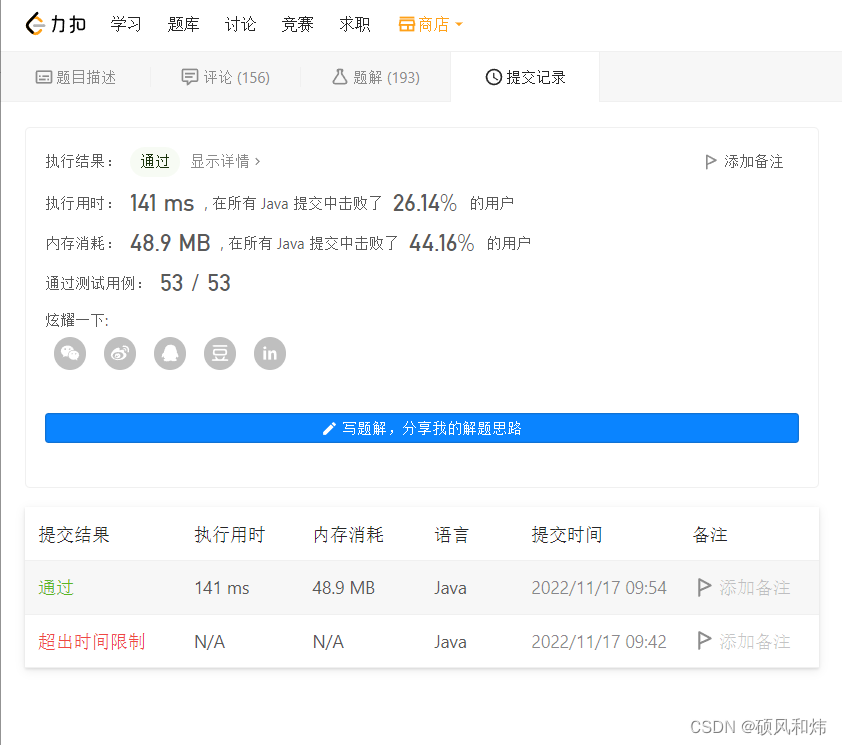
运行结果2：