【C++进阶】map和set——中篇（AVL树的学习）

news2024/11/18 11:32:26

🎇C++笔试强训

  • 博客主页：一起去看日落吗
  • 分享博主的C++刷题日常，大家一起学习
  • 博主的能力有限，出现错误希望大家不吝赐教
  • 分享给大家一句我很喜欢的话：夜色难免微凉，前方必有曙光 🌞。

在这里插入图片描述

🍁 🍃 🍂 🌿

目录

  • 🍁 前言
  • 🍁 1. AVL树
    • 🍂 1.1 AVL树的概念
    • 🍂 1.2 AVL树节点的定义
    • 🍂 1.3 AVL树的插入
    • 🍂 1.4 AVL树的旋转
    • 🍂 1.5 AVL树的验证
    • 🍂 1.6 AVL树的性能
    • 🍂 1.7 AVL树的实现

🍁 前言

前面对map/multimap/set/multiset进行了简单的介绍，在其文档介绍中发现，这几个容器有个
共同点是：其底层都是按照二叉搜索树来实现的，但是二叉搜索树有其自身的缺陷，假如往树中
插入的元素有序或者接近有序，二叉搜索树就会退化成单支树，时间复杂度会退化成O(N)，因此
map、set等关联式容器的底层结构是对二叉树进行了平衡处理，即采用平衡树来实现。

🍁 1. AVL树

🍂 1.1 AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

  • 一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

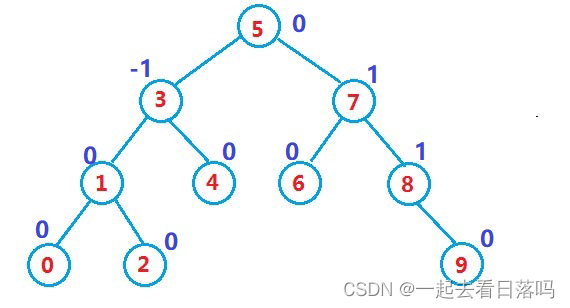
在这里插入图片描述

如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在
O ( l o g 2 n ) O(log_2 n) O(log2​n)，搜索时间复杂度O( l o g 2 n log_2 n log2​n)。

🍂 1.2 AVL树节点的定义

template<class T>
struct AVLTreeNode
{
	AVLTreeNode(const T& data)
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data), _bf(0)
	{}
	
	AVLTreeNode<T>* _pLeft; // 该节点的左孩子
	AVLTreeNode<T>* _pRight; // 该节点的右孩子
	AVLTreeNode<T>* _pParent; // 该节点的双亲
	T _data;
	int _bf; // 该节点的平衡因子
};

🍂 1.3 AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么
AVL树的插入过程可以分为两步：

  1. 按照二叉搜索树的方式插入新节点
  2. 调整节点的平衡因子

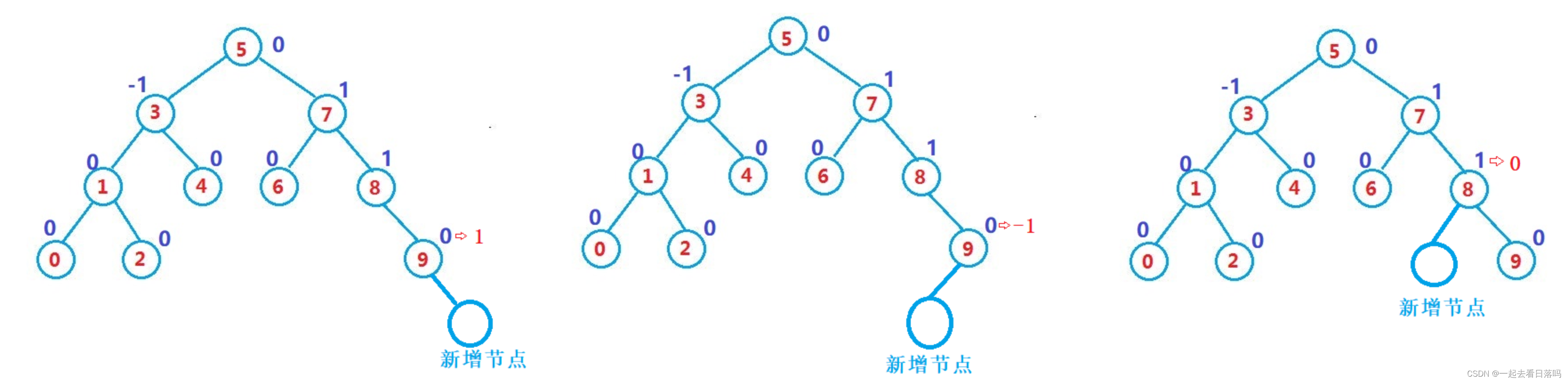
在这里插入图片描述
pCur插入后，pParent的平衡因子一定需要调整，在插入之前，pParent的平衡因子分为三种情况：
-1，0, 1, 分以下两种情况：

  1. 如果pCur插入到pParent的左侧，只需给pParent的平衡因子-1即可
  2. 如果pCur插入到pParent的右侧，只需给pParent的平衡因子+1即可

此时：pParent的平衡因子可能有三种情况：0，正负1， 正负2

  1. 如果pParent的平衡因子为0，说明插入之前pParent的平衡因子为正负1，插入后被调整
    成0，此时满足AVL树的性质，插入成功
  2. 如果pParent的平衡因子为正负1，说明插入前pParent的平衡因子一定为0，插入后被更
    新成正负1，此时以pParent为根的树的高度增加，需要继续向上更新
  3. 如果pParent的平衡因子为正负2，则pParent的平衡因子违反平衡树的性质，需要对其进
    行旋转处理
pair<Node*,bool> Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)//根节点为空时先new一个新节点
		{
			_root = new Node(kv);
			return make_pair(_root, true);
		}
 
		Node* cur = _root;
		Node* parent = nullptr;
		//先利用while循环去找cur的空位
		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return make_pair(cur, false);
			}
		}
		//将cur插入到相应位置
		cur = new Node(kv);
		Node* newnode = cur;//用一个newnode记录一下新节点用以返回
		if (kv.first > parent->_kv.first)
		{
			parent->_right = cur;//注意三叉链的链接逻辑顺序,等号左右方向不能反，先把cur链接到父节点的右边
			cur->_parent = parent;//然后再去把父指针知道父节点
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}
 
		//进行旋转调整
		//while(cur!=_root)
		while (parent)
		{
			//1.进入循环先对平衡因子进行调整
			if (cur == parent->_right)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}
 
			//分三种情况向上走
			if (parent->_bf == 0)//平衡因子等于0不需要调整
			{
				//为什么不需调整
				//因为等于0的话，说明底层子树高度不平衡，添加进入新元素后平衡了，只要平衡了高度并没发生变化，不会影响上面的父节点
				break;
			}
			else if (parent->_bf == -1 || parent->_bf == 1)
			{
				//平衡因子等于-1，说明插入新节点后子树的高度不平衡了，需要继续往上迭代查看父节点是否还满足平衡节点
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				if (parent->_bf == -2)//父节点等于-2，说明左边高，触发右旋的情况
				{
					if (cur->_bf == -1)//cur节点等于-1，说明在cur的左边更高，触发右单旋的情况
					{
						RotateR(parent);
					}
					else//cur等于-1,说明在cur的右边更高，触发左右双旋
					{
						RotateLR(parent);
					}
				}
				else//父节点等于1，说明右边更高，触发左旋的情况
				{
					if (cur->_bf == 1)//cur节点等于1时，说明在cur的右边更高，触发右单旋的情况
					{
						RotateL(parent);
					}
					else//cur等于-1,说明在cur的左边更高，触发右左双旋
					{
						RotateRL(parent);
					}
				}
				//思考：为什么上面在传参数的时候，都是传parent的节点呢？这样的好处是什么呢
 
				break;//调整完成后break退出循环
				//这里为什么调整完成过后就可以退出，通过旋转调整平衡因子后，parent节点的平衡因子都为0了，调整过后不需要再向上继续查找了
			}
			else
			{
				assert(false);
			}
		}
		return make_pair(newnode,true);
	}

🍂 1.4 AVL树的旋转

如果在一棵原本是平衡的AVL树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。根据节点插入位置的不同，AVL树的旋转分为四种：

  • 新节点插入较高左子树的左侧—左左：右单旋

在这里插入图片描述

上图在插入前，AVL树是平衡的，新节点插入到30的左子树(注意：此处不是左孩子)中，30左子树增加了一层，导致以60为根的二叉树不平衡，要让60平衡，只能将60左子树的高度减少一层，右子树增加一层，即将左子树往上提，这样60转下来，因为60比30大，只能将其放在30的右子树，而如果30有
右子树，右子树根的值一定大于30，小于60，只能将其放在60的左子树，旋转完成后，更新节点的平衡因子即可。在旋转过程中，有以下几种情况需要考虑：

  1. 30节点的右孩子可能存在，也可能不存在
  2. 60可能是根节点，也可能是子树

如果是根节点，旋转完成后，要更新根节点

如果是子树，可能是某个节点的左子树，也可能是右子树

void RotateR(Node* parent)//右单旋
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
 
		parent->_left = subLR;
		if (subLR != nullptr)//注意:这里一定要判断不为空的，因为下面可能会出现空指针的解引用
		{
			subLR->_parent = parent;
		}
		subL->_right = parent;
		Node* parentParent = parent->_parent;//一定要在改变链接关系之前把这个指针存下来
		parent->_parent = subL;
		
		//if (parentParent == nullptr)或者采用这个条件也是可以的
		if(parent==_root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			//这里注意:parent还有父母时，链接之前需要注意判断到底是右孩子还是左孩子
			if (parentParent->_left == parent)
				parentParent->_left = subL;
			else
				parentParent->_right = subL;
 
			subL->_parent = parentParent;//最后还要把父指针关系链接上
		}
 
		parent->_bf = subL->_bf = 0;//最后右单旋完成后平衡因子都要修改成0
	}
  • 新节点插入较高右子树的右侧—右右：左单旋

在这里插入图片描述

和右单旋近似，可以参考代码

void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
 
		//先把subR的左孩子赋值给parent的右节点
		parent->_right = subRL;
		if (subRL != nullptr)//注意一定要判断是否为空的情况
		{
			subRL->_parent = parent;//然后链接parent指针
		}
 
		//然后subR的左节点链接上parent
		subR->_left = parent;
		Node* parentParent = parent->_parent;//提前记录
		parent->_parent = subR;
		//if (parentParent == nullptr)
		if (parent == _root)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
				parentParent->_left = subR;
			else
				parentParent->_right = subR;
 
			subR->_parent = parentParent;
		}
 
		parent->_bf = subR->_bf = 0;
	}
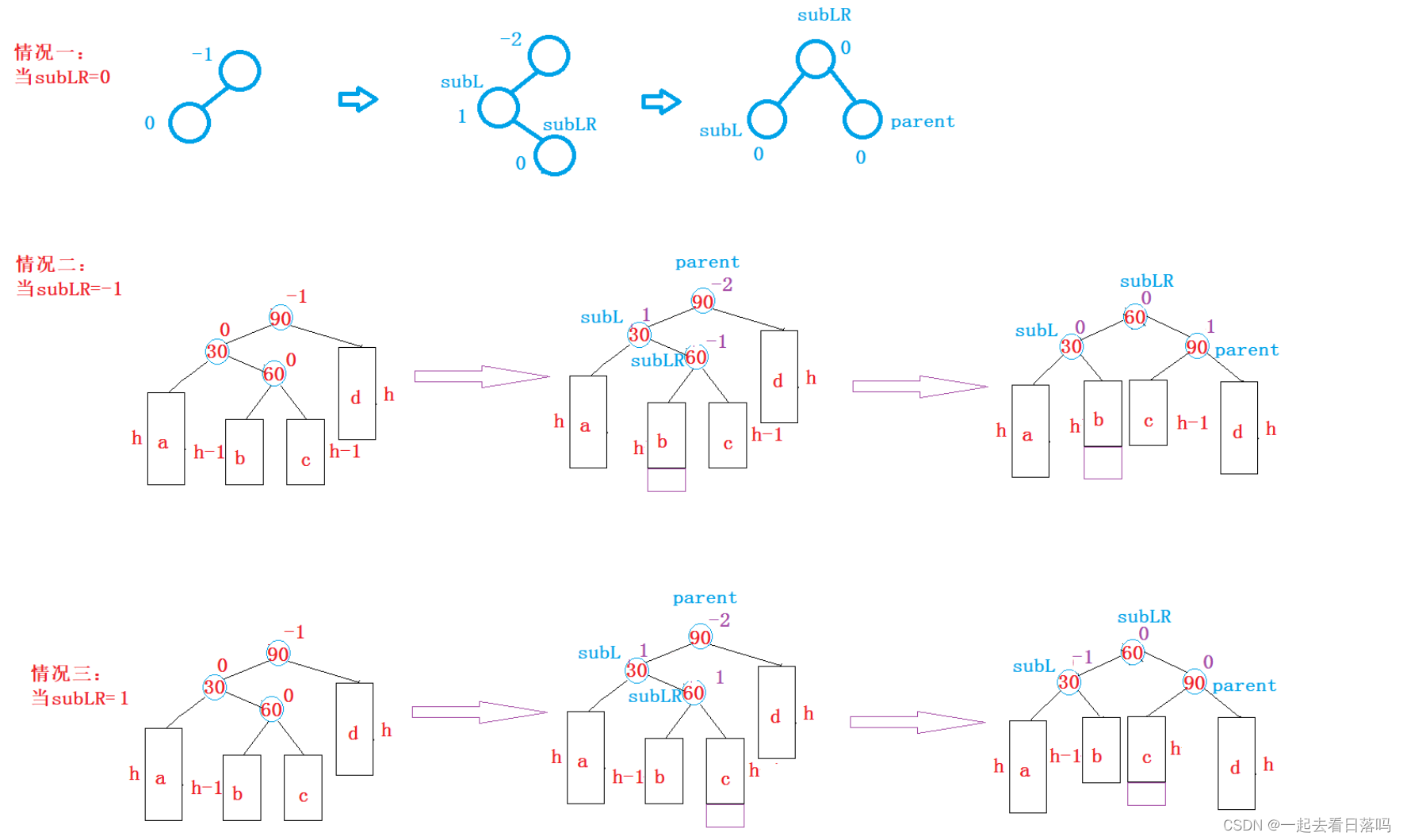
  • 新节点插入较高左子树的右侧—左右：先左单旋再右单旋

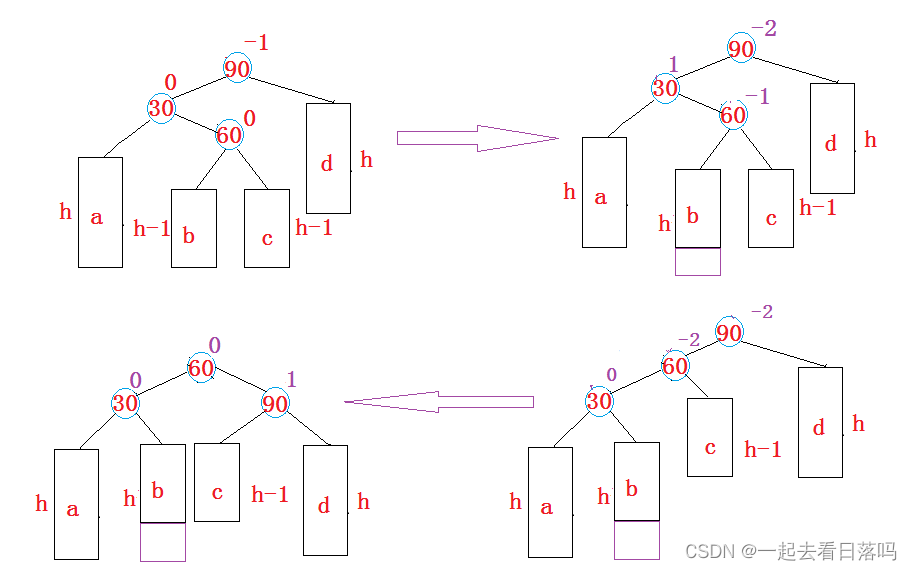
在这里插入图片描述
将双旋变成单旋后再旋转，即：先对30进行左单旋，然后再对90进行右单旋，旋转完成后再
考虑平衡因子的更新。

请添加图片描述

void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
		RotateL(parent->_left);//先进行左旋，并注意旋转点为父节点的左节点
		RotateR(parent);//再进行右旋，此时旋转点为父节点
 
		if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}//注意这里处理完成过后sunRL的平衡因子一定都是等于0的
		else
		{
			assert(false);
		}
	}
  • 新节点插入较高右子树的左侧—右左：先右单旋再左单旋

在这里插入图片描述

void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;//注意：需要提前存subRL的平衡因子，因为旋转可能引起改变
		//subRL的平衡因子是双旋的关键节点
 
		RotateR(parent->_right);//先进行右旋，并注意旋转点为父节点的右节点
		RotateL(parent);//再进行左旋，此时旋转点为父节点
 
		if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}//注意这里处理完成过后sunRL的平衡因子一定都是等于0的
		else
		{
			assert(false);
		}
	}

总结：
假如以pParent为根的子树不平衡，即pParent的平衡因子为2或者-2，分以下情况考虑

  1. pParent的平衡因子为2，说明pParent的右子树高，设pParent的右子树的根为pSubR
    – 当pSubR的平衡因子为1时，执行左单旋
    – 当pSubR的平衡因子为-1时，执行右左双旋
  2. pParent的平衡因子为-2，说明pParent的左子树高，设pParent的左子树的根为pSubL
    – 当pSubL的平衡因子为-1是，执行右单旋
    – 当pSubL的平衡因子为1时，执行左右双旋

旋转完成后，原pParent为根的子树个高度降低，已经平衡，不需要再向上更新。

🍂 1.5 AVL树的验证

AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分两步：

  1. 验证其为二叉搜索树
    – 如果中序遍历可得到一个有序的序列，就说明为二叉搜索树
  2. 验证其为平衡树
    – 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
    – 节点的平衡因子是否计算正确
void _Inorder(Node* root)//中序遍历打印每个节点
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_Inorder(root->_right);
	}
	void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}
 
	//验证是否为平衡二叉树
	//1.左子树高度与右子树高度差必须小于1
	int _Height(Node* root)//求树的高度函数
	{
		if (root == nullptr)
		{
			return 0;
		}
 
		int leftHeight = _Height(root->_left);//递归去子问题求解
		int rightHeight = _Height(root->_right);
 
		return rightHeight > leftHeight ? rightHeight + 1 : leftHeight + 1;
	}
	bool _IsBalance(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}
 
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
 
		// 2.检查一下每颗树的平衡因子是否正确
		if (rightHeight - leftHeight != root->_bf)
		{
			cout << "平衡因子异常:" << root->_kv.first << endl;
			return false;
		}
 
		return abs(rightHeight - leftHeight) < 2
			&& _IsBalance(root->_left)
			&& _IsBalance(root->_right);//分别递归到各自的左右子树再去检查
	}
	bool IsAVLTree()
	{
		return _IsBalance(_root);
	}

🍂 1.6 AVL树的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这
样可以保证查询时高效的时间复杂度，即 l o g 2 ( N ) log_2 (N) log2​(N)。

但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

🍂 1.7 AVL树的实现

AVLTree.hpp

//
//  AVLTree.hpp
//  AVLtree
//
//  Created by 卜绎皓 on 2022/11/16.
//

#pragma once
#include<iostream>
#include<assert.h>
#include<string>
using namespace std;
 
 
template<class K,class V>
struct AVLTreeNode
{
    AVLTreeNode<K, V>* _left;
    AVLTreeNode<K, V>* _right;
    AVLTreeNode<K, V>* _parent;//定义成三叉链的形式
    int _bf;//balance factor平衡因子
    pair<K, V> _kv;//用pair同时存K和V两个数据
 
    AVLTreeNode(const pair<K,V>& kv)//节点构造函数
        :_left(nullptr)
        ,_right(nullptr)
        ,_parent(nullptr)
        ,_bf(0)//平衡因子初始给0
        ,_kv(kv)
    {}
};
 
template<class K,class V>
class AVLTree
{
    typedef AVLTreeNode<K, V> Node;
public:
    AVLTree()
        :_root(nullptr)
    {}
    //拷贝构造和赋值拷贝也需要自己实现
    AVLTree(const AVLTree<K,V>& kv)
    {
        _root = Copy(kv._root);
    }
    AVLTree<K, V>& operator=(AVLTree<K,V> kv)
    {
        swap(_root, kv._root);
        return *this;
    }
    ~AVLTree()
    {
        Destroy(_root);
        _root = nullptr;
    }
    Node* Copy(Node* root)
    {
        if (root == nullptr)
            return nullptr;
        Node* newroot = new Node(root->_key);//建立新节点
        newroot->_left = Copy(root->_left);//新节点的左右节点再去转换成子问题
        newroot->_right = Copy(root->_right);
        return newroot;//最后返回新节点
    }
    void Destroy(Node* root)
    {
        //利用后序遍历去释放节点
        if (root == nullptr)
        {
            return;
        }
        Destroy(root->_left);
        Destroy(root->_right);
        delete root;
    }
    V& operator[](const K& key)//重载operator[]
    {
        //operator[]的原则是:
        //如果插入成功返回插入都value的引用
        //如果插入失败则返回V类型默认缺省值
        pair<Node*, bool> ret = Insert(make_pair(key, V()));//V采用传匿名对象的方式
        return ret.first->_kv.second;
    }
    Node* Find(const pair<K, V>& kv)//查找函数
    {
        Node* cur = _root;
        while (cur)
        {
            if (kv.first > cur->_kv.first)
            {
                cur = cur->_right;
            }
            else if (kv.first < cur->_kv.first)
            {
                cur = cur->_left;
            }
            else
            {
                return cur;
            }
        }
        return nullptr;
    }
    void RotateR(Node* parent)//右单旋
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;
 
        parent->_left = subLR;
        if (subLR != nullptr)//注意:这里一定要判断不为空的，因为下面可能会出现空指针的解引用
        {
            subLR->_parent = parent;
        }
        subL->_right = parent;
        Node* parentParent = parent->_parent;//一定要在改变链接关系之前把这个指针存下来
        parent->_parent = subL;
        
        //if (parentParent == nullptr)或者采用这个条件也是可以的
        if(parent==_root)
        {
            _root = subL;
            _root->_parent = nullptr;
        }
        else
        {
            //这里注意:parent还有父母时，链接之前需要注意判断到底是右孩子还是左孩子
            if (parentParent->_left == parent)
                parentParent->_left = subL;
            else
                parentParent->_right = subL;
 
            subL->_parent = parentParent;//最后还要把父指针关系链接上
        }
 
        parent->_bf = subL->_bf = 0;//最后右单旋完成后平衡因子都要修改成0
    }
    void RotateL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;
 
        //先把subR的左孩子赋值给parent的右节点
        parent->_right = subRL;
        if (subRL != nullptr)//注意一定要判断是否为空的情况
        {
            subRL->_parent = parent;//然后链接parent指针
        }
 
        //然后subR的左节点链接上parent
        subR->_left = parent;
        Node* parentParent = parent->_parent;//提前记录
        parent->_parent = subR;
        //if (parentParent == nullptr)
        if (parent == _root)
        {
            _root = subR;
            _root->_parent = nullptr;
        }
        else
        {
            if (parentParent->_left == parent)
                parentParent->_left = subR;
            else
                parentParent->_right = subR;
 
            subR->_parent = parentParent;
        }
 
        parent->_bf = subR->_bf = 0;
    }
    void RotateRL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;
        int bf = subRL->_bf;//注意：需要提前存subRL的平衡因子，因为旋转可能引起改变
        //subRL的平衡因子是双旋的关键节点
 
        RotateR(parent->_right);//先进行右旋，并注意旋转点为父节点的右节点
        RotateL(parent);//再进行左旋，此时旋转点为父节点
 
        if (bf == 0)
        {
            parent->_bf = 0;
            subR->_bf = 0;
            subRL->_bf = 0;
        }
        else if (bf == 1)
        {
            parent->_bf = -1;
            subR->_bf = 0;
            subRL->_bf = 0;
        }
        else if (bf == -1)
        {
            parent->_bf = 0;
            subR->_bf = 1;
            subRL->_bf = 0;
        }//注意这里处理完成过后sunRL的平衡因子一定都是等于0的
        else
        {
            assert(false);
        }
    }
    void RotateLR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;
        int bf = subLR->_bf;
        RotateL(parent->_left);//先进行左旋，并注意旋转点为父节点的左节点
        RotateR(parent);//再进行右旋，此时旋转点为父节点
 
        if (bf == 0)
        {
            parent->_bf = 0;
            subL->_bf = 0;
            subLR->_bf = 0;
        }
        else if (bf == 1)
        {
            parent->_bf = 0;
            subL->_bf = -1;
            subLR->_bf = 0;
        }
        else if (bf == -1)
        {
            parent->_bf = 1;
            subL->_bf = 0;
            subLR->_bf = 0;
        }//注意这里处理完成过后sunRL的平衡因子一定都是等于0的
        else
        {
            assert(false);
        }
    }
    pair<Node*,bool> Insert(const pair<K, V>& kv)
    {
        if (_root == nullptr)//根节点为空时先new一个新节点
        {
            _root = new Node(kv);
            return make_pair(_root, true);
        }
 
        Node* cur = _root;
        Node* parent = nullptr;
        //先利用while循环去找cur的空位
        while (cur)
        {
            if (kv.first > cur->_kv.first)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (kv.first < cur->_kv.first)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return make_pair(cur, false);
            }
        }
        //将cur插入到相应位置
        cur = new Node(kv);
        Node* newnode = cur;//用一个newnode记录一下新节点用以返回
        if (kv.first > parent->_kv.first)
        {
            parent->_right = cur;//注意三叉链的链接逻辑顺序,等号左右方向不能反，先把cur链接到父节点的右边
            cur->_parent = parent;//然后再去把父指针知道父节点
        }
        else
        {
            parent->_left = cur;
            cur->_parent = parent;
        }
 
        //进行旋转调整
        //while(cur!=_root)
        while (parent)
        {
            //1.进入循环先对平衡因子进行调整
            if (cur == parent->_right)
            {
                parent->_bf++;
            }
            else
            {
                parent->_bf--;
            }
 
            //分三种情况向上走
            if (parent->_bf == 0)//平衡因子等于0不需要调整
            {
                //为什么不需调整
                //因为等于0的话，说明底层子树高度不平衡，添加进入新元素后平衡了，只要平衡了高度并没发生变化，不会影响上面的父节点
                break;
            }
            else if (parent->_bf == -1 || parent->_bf == 1)
            {
                //平衡因子等于-1，说明插入新节点后子树的高度不平衡了，需要继续往上迭代查看父节点是否还满足平衡节点
                cur = parent;
                parent = parent->_parent;
            }
            else if (parent->_bf == 2 || parent->_bf == -2)
            {
                if (parent->_bf == -2)//父节点等于-2，说明左边高，触发右旋的情况
                {
                    if (cur->_bf == -1)//cur节点等于-1，说明在cur的左边更高，触发右单旋的情况
                    {
                        RotateR(parent);
                    }
                    else//cur等于-1,说明在cur的右边更高，触发左右双旋
                    {
                        RotateLR(parent);
                    }
                }
                else//父节点等于1，说明右边更高，触发左旋的情况
                {
                    if (cur->_bf == 1)//cur节点等于1时，说明在cur的右边更高，触发右单旋的情况
                    {
                        RotateL(parent);
                    }
                    else//cur等于-1,说明在cur的左边更高，触发右左双旋
                    {
                        RotateRL(parent);
                    }
                }
                //思考：为什么上面在传参数的时候，都是传parent的节点呢？这样的好处是什么呢
 
                break;//调整完成后break退出循环
                //这里为什么调整完成过后就可以退出，通过旋转调整平衡因子后，parent节点的平衡因子都为0了，调整过后不需要再向上继续查找了
            }
            else
            {
                assert(false);
            }
        }
        return make_pair(newnode,true);
    }
    void _Inorder(Node* root)//中序遍历打印每个节点
    {
        if (root == nullptr)
            return;
        _Inorder(root->_left);
        cout << root->_kv.first << ":" << root->_kv.second << endl;
        _Inorder(root->_right);
    }
    void Inorder()
    {
        _Inorder(_root);
        cout << endl;
    }
 
    //验证是否为平衡二叉树
    //1.左子树高度与右子树高度差必须小于1
    int _Height(Node* root)//求树的高度函数
    {
        if (root == nullptr)
        {
            return 0;
        }
 
        int leftHeight = _Height(root->_left);//递归去子问题求解
        int rightHeight = _Height(root->_right);
 
        return rightHeight > leftHeight ? rightHeight + 1 : leftHeight + 1;
    }
    bool _IsBalance(Node* root)
    {
        if (root == nullptr)
        {
            return true;
        }
 
        int leftHeight = _Height(root->_left);
        int rightHeight = _Height(root->_right);
 
        // 2.检查一下每颗树的平衡因子是否正确
        if (rightHeight - leftHeight != root->_bf)
        {
            cout << "平衡因子异常:" << root->_kv.first << endl;
            return false;
        }
 
        return abs(rightHeight - leftHeight) < 2
            && _IsBalance(root->_left)
            && _IsBalance(root->_right);//分别递归到各自的左右子树再去检查
    }
    bool IsAVLTree()
    {
        return _IsBalance(_root);
    }
private:
    Node* _root;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/11499.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

第8章 数据库连接池

第8章 数据库连接池

*数据库连接池的基本思想&#xff1a;为数据库建立一个缓冲池&#xff0c;预先在缓冲池中放入一定数量的连接&#xff0c;当需要建立数据库连接时&#xff0c;只需要从缓冲池中取出一个&#xff0c;使用完毕后再放回 *数据库连接池负责分配、管理和释放数据库连接&#xff0c;…
阅读更多...
Java 变量和数据类型

Java 变量和数据类型

Java 变量和数据类型Java 变量Java变量概念变量使用的基本步骤案例&#xff1a;输出人的信息&#xff08;年龄&#xff0c;成绩&#xff0c;性别&#xff0c;姓名&#xff09;变量使用注意事项案例&#xff1a;变量使用注意事项程序中 号的使用案例数据类型整数类型基本介绍案…
阅读更多...
Spring Bean的生命周期源码解析

Spring Bean的生命周期源码解析

文章目录前言零、Bean生命周期流程图一、加载类二、实例化前2.1、使用案例2.2、源码---InstantiationAwareBeanPostProcessor.postProcessBeforeInstantiation()三、实例化3.1、Supplier创建对象3.2、工厂方法创建对象3.3、推断构造方法3.4、源码四、BeanDefinition的后置处理4…
阅读更多...
在Ubuntu下安装地球物理学专业软件madagascar

在Ubuntu下安装地球物理学专业软件madagascar

1.下载安装文件 git clone https://github.com/ahay/src RSFSRC这一步搞好后会在当前路径下生成RSFSRC 文件夹 2.预安装 安装依赖软件 sudo apt-get install libxaw7-dev freeglut3-dev libnetpbm10-dev libgd-dev \ libplplot-dev libavcodec-dev libcairo2-dev libjpeg-d…
阅读更多...
（设计模式）工厂模式

（设计模式）工厂模式

工厂模式 工厂模式&#xff08;Factory Pattern&#xff09;是 Java 中最常用的设计模式之一。这种类型的设计模式属于创建型模式&#xff0c;它提供了一种创建对象的最佳方式。 在工厂模式中&#xff0c;我们在创建对象时不会对客户端暴露创建逻辑&#xff0c;并且是通过使用…
阅读更多...
【C++】C++基础知识（五）---数组

【C++】C++基础知识（五）---数组

C基础知识&#xff08;五&#xff09;1. 一维数组1.1 定义方式1.2 数组名用途1.3 案例分析2. 二维数组2.1 定义方式2.2 数组名用途2.3 案例分析3. 多维数组1. 一维数组 数组就是一个集合&#xff0c;里面存放了相同类型的数据元素。 特点&#xff1a; 1、数组中每个元素的数据…
阅读更多...
探究并发和并行、同步和异步、进程和线程、阻塞和非阻塞、响应和吞吐等

探究并发和并行、同步和异步、进程和线程、阻塞和非阻塞、响应和吞吐等

一. 并发和并行 操作系统扫盲&#xff1a; 1. 对于单核cpu而言(不管单核单线程也好&#xff0c;单核多线程也罢)&#xff0c;同一时间只能干一件事&#xff01;&#xff01;为了看起像可以“同时干多件事”&#xff0c;windows操作系统把cpu的时间划分为长短基本相同的时间区间…
阅读更多...
Golang入门笔记（3）—— 运算符

Golang入门笔记（3）—— 运算符

本来这块代码&#xff0c;作为有了一点语言基础的人是真不想写的&#xff0c;因为和其他语言没有什么不同的地方&#xff0c;但是就怕 真的还有人看我的帖子&#xff0c;还真怕真的有初学者在看我帖子&#xff0c;所以还是贴心的抄了一遍。 和Java不同的地方 1. &变量取地址…
阅读更多...
【Spring】一文带你吃透基于XML的DI技术

【Spring】一文带你吃透基于XML的DI技术

个人主页&#xff1a; 几分醉意的CSDN博客_传送门 文章目录&#x1f496;基于XML的DI✨set注入&#x1f4ab;基本语法&#x1f4ab;和属性名无关&#x1f4ab;给非自定义类属性赋值&#x1f4ab;引用类型注入✨构造注入&#x1f4ab;name属性&#x1f4ab;index属性✨引用类型的…
阅读更多...
哈希表(hash_table)的原理

哈希表(hash_table)的原理

一、hash_table的介绍 hash_table可提供对任何键值对的存取和删除操作。由于操作对象是键值对&#xff0c;所以hash table也可被视为一种字典结构(dictionary)。这种结构的用意在于提供常数时间的基本操作&#xff0c;就像stack或queue那样。乍听之下这几乎是不可能的任务&…
阅读更多...
SpringBoot中使用Redis实现分布式锁

SpringBoot中使用Redis实现分布式锁

文章目录一。Redis实现分布式锁原理二。代码实现Redis分布式锁一。Redis实现分布式锁原理 以下内容为转载部分&#xff0c;主要介绍Redis实现分布式锁的背景&#xff1a; 转载博客&#xff1a;https://blog.csdn.net/fuzhongmin05/article/details/119251590 为什么需要分布式…
阅读更多...
[附源码]计算机毕业设计JAVA高校创新创业项目管理系统

[附源码]计算机毕业设计JAVA高校创新创业项目管理系统

[附源码]计算机毕业设计JAVA高校创新创业项目管理系统 项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM…
阅读更多...
数字化转型重塑企业竞争优势，SaaS电商系统助力锂电池行业实现降本增效

数字化转型重塑企业竞争优势，SaaS电商系统助力锂电池行业实现降本增效

作为我国核心基础工业的关键材料之一&#xff0c;锂电池在汽车、医疗器械、航天航空、消费类电子产品等领域均可发挥重要作用。近年来&#xff0c;随着新能源汽车的快速发展有力带动了锂电池行业的市场需求&#xff0c;锂电池已成为化学电源应用领域中最具竞争力的电池&#xf…
阅读更多...
Vue | Vue.js 实现过渡动画

Vue | Vue.js 实现过渡动画

&#x1f5a5;️ Vue .js专栏&#xff1a;Vue .js 实现过渡动画 &#x1f9d1;‍&#x1f4bc; 个人简介&#xff1a;一个不甘平庸的平凡人&#x1f36c; ✨ 个人主页&#xff1a;CoderHing的个人主页 &#x1f340; 格言: ☀️ 路漫漫其修远兮,吾将上下而求索☀️ &#x1f44…
阅读更多...
基于51单片机的智能路灯控制系统proteus仿真原理图PCB

基于51单片机的智能路灯控制系统proteus仿真原理图PCB

功能&#xff1a; 0.本系统采用STC89C52作为单片机 1.LCD1602液晶实时显示当前时间/环境光强/工作模式 2.支持路灯故障检测 3.工作时间内(17~24时)&#xff0c;两个路灯同时点亮&#xff0c;24时以后&#xff0c;B路灯关闭&#xff0c;若检测到由物体通过&#xff0c;路灯B点亮…
阅读更多...
R17 redcap

R17 redcap

微信同步更新欢迎关注同名modem协议笔记 在5G时代&#xff0c;某些场景的终端并不需要特别复杂&#xff0c;只要满足成本低&#xff0c;功耗小&#xff0c;尺寸小等要求即可&#xff0c;例如视频监控&#xff0c;可穿戴设备&#xff0c;工业无线传感器等&#xff0c;redcap就是…
阅读更多...
electron vue 模仿qq登录界面

electron vue 模仿qq登录界面

1、使用vuecli创建vue项目 我用的vue2 vue create qq_test2、安装electron npm install electron -g //or npm install electron12.0.11 //老版本3、vue项目安装Electron-builder打包工具 版本我选择的是12 vue add electron-builder4、在vue项目的src下有个background.…
阅读更多...
收藏｜多指标时序预测方式及时序特征工程总结

收藏｜多指标时序预测方式及时序特征工程总结

背景 现如今&#xff0c;随着企业业务系统越来越复杂&#xff0c;单指标时间序列预测已不能满足大部分企业需求。在复杂的系统内&#xff0c;如果采用单一的指标进行时间序列预测&#xff0c;由于各个指标相互作用的关系&#xff0c;因此会因为漏掉部分指标因素导致出现预测精…
阅读更多...
进程间的通信 - 剪切板

进程间的通信 - 剪切板

剪切板是系统维护管理的一块内存区域&#xff0c;本机的所有进程都可以访问。当一个进程复制数据时&#xff0c;先将数据放在该内存区&#xff0c;当另一个进程粘贴时&#xff0c;则是从该内存区块取出数据 剪切板操作&#xff1a; 其实在剪切板中也就那几个API在使用&#x…
阅读更多...
tf模型落地安卓之旧事重提

tf模型落地安卓之旧事重提

之前将tf模型落地安卓了&#xff0c;其实就是clone一下官方的代码&#xff0c;然后配置下环境就打包了&#xff0c;没啥技术含量&#xff0c;现在再看&#xff0c;问题就在环境配置了。 1&#xff0c;Unable to start the daemon process. Q Group 277356808 The project use…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023