目录

堆栈与队列算法-八皇后问题的求解算法

C++代码

---

堆栈与队列算法-八皇后问题的求解算法

八皇后问题是一种常见的堆栈应用实例。在国际象棋中的皇后可以在没有限定一步走几格的前提下，对棋盘中的其他棋子直吃、横吃和对角斜吃（左斜吃或右斜吃均可）。现在要放入多个皇后到棋盘上，相互之间不能互相吃到对方。后放入的新皇后，放入前必须考虑所放位置的直线方向、横线方向或对角线方向是否已被放置了旧皇后，否则就会被先放入的旧皇后吃掉。

利用这种概念，我们将其应用到4X4的棋盘上，就称为四皇后问题；应用在8X8的棋盘上，就称为八皇后问题；应用在NXN的棋盘上，就称为N皇后问题。要解决N皇后问题（在此我们以八皇后为例），首先在棋盘中放入一个新皇后，且不会被先前放置的旧皇后吃掉，然后这个新皇后的位置压入堆栈。

如果放置新皇后的该行（或该列）的8个位置都没有办法放置新皇后（放入任何一个位置都会被先前放置的旧皇后吃掉），就必须从堆栈中弹出前一个皇后的位置，并在该行（或该列）中重新寻找一个新的位置，再将该位置压入堆栈中，这种方式就是一种回溯算法的应用。

N皇后问题的解答就是结合堆栈和回溯两种数据结构，以逐行（或逐列）寻找新皇后合适的位置（如果找不到，就回溯到前一行寻找前一个皇后的另一个新位置，依此类推）的方式来寻找N皇后问题的其中一组解答。

C++代码

#include<iostream>
using namespace std;

class Queen {
private:
	int Num;
	int Count;
	int* queenList;
public:
	Queen(int tempNum) {
		this->Num = tempNum;
		Count = 0;
		queenList = new int[Num] {0};
	}

	bool Attack(int row, int col) {
		bool beAttack = false;
		int i = 0;
		int offsetRow = 0;
		int offsetCol = 0;
		while (!beAttack && i<col) {
			offsetCol = abs(i - col);
			offsetRow = abs(queenList[i] - row);
			if (queenList[i] == row || (offsetRow == offsetCol))
				beAttack = true;
			i++;
		}
		return beAttack;
	}

	void PrintTable() {
		Count += 1;
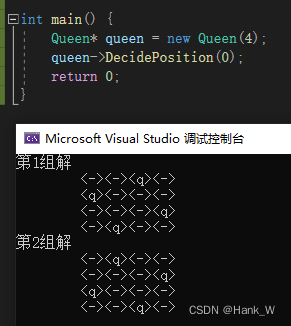
		cout << "第" << Count << "组解" << endl;
		for (int x = 0; x < Num; x++) {
			cout << "\t";
			for (int y = 0; y < Num; y++) {
				if (x == queenList[y])
					cout << "<q>";
				else
					cout << "<->";
			}
			cout << endl;
		}
		system("pause");
	}

	void DecidePosition(int val) {
		int i = 0;
		while (i < Num) {
			if (!Attack(i, val)) {
				queenList[val] = i;
				if (val == (Num - 1))
					PrintTable();
				else
					DecidePosition(val + 1);
			}
			i++;
		}
	}
};

int main() {
	Queen* queen = new Queen(8);
	queen->DecidePosition(0);
	return 0;
}

输出结果

其他的N皇后测试结果