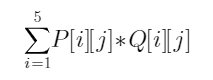点赞收藏,以防遗忘
本文【程序大视界】已收录,关注免费领取互联网大厂学习资料,添加博主好友进群学习交流,欢迎留言和评论,一起交流共同进步。
目录
【一】前言
【二】打家劫舍
【三】不同路径
【四】最小路径和
【五】零钱兑换
【二】总结
【一】前言
算法编程里面动态规划可谓是一个必须要掌握的一大算法题型了,它充分考察一个人的数据建模与分析能力、抽象思维以及边界,利用递推的思维动态求解出结果。
【二】打家劫舍
【题目】:你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
【解解】:
- 首先考虑边界条件,如果只有一间房屋则只能偷窃该房屋,如果有2间房屋,因为相邻的房屋不能同时偷窃,所以只能一间,选择偷窃金额较高的那间。
- 当房间数大于2的时候,对于k(k>2)间房屋,有两个选项:
- 偷窃第k间房屋,那么就不能偷窃第k-1间房屋,偷窃总金额为前k-2间房屋的最高总金额与第k间房屋的金额之和
- 不偷窃第k间房屋,偷窃总金额为前k-1间房屋的最高总金额。
两个选项中选择偷窃总金额较大的选项,该选项对应的偷窃金额即为前k间房屋能偷窃到的最高总金额
用dp[i]表示前i间房屋能偷窃到的最高总金额,递推公式:
dp[i] =max(dp[i-2]+nums[i],dp[i-1])
边界条件:dp[0]=nums[0] 只有一间房屋、dp[1]=max(nums[0],nums[1]) 两间房屋选择金额较大的那间
class Solution {
public int rob(int[] nums) {
if(nums == null || nums.length ==0){
return 0;//如果数组为空直接返回0
}
int len = nums.length;
if(len == 1){
return nums[0];//如果数组只有一个元素直接返回第一个元素
}
int[] dp = new int[len];//创建结果数组,长度为原数组长度
dp[0] = nums[0];//设置结果数组第一个元素为原数组第一个元素
dp[1] = Math.max(nums[1],nums[0]);//设置结果数组第二个元素为原数组中第一个与第二个中的最大值
for(int i =2; i<len; i++){
dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1]);//递推公式:dp[i]的值为dp[i-2]+原数组中第i个元素值 跟 dp[i-1]的最大值
}
return dp[len-1];//返回最后一个元素,注意由于计算结果是相邻元素不能计算,所以结果数组中最后一个元素为len-1
}
} 【三】不同路径
【题目】:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28
示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3 输出:28
示例 4:
输入:m = 3, n = 3 输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
【解答】:因为机器人只能向右或者向下移动一格,以终为始假设机器人已经到达最右下脚的位置,则它有2个方案到达这个位置,一个是正上方的格子向下移动一格,另一个是左边的格子向右移动一格。用二维数组int[i][j] f表示为到达第i行第j列这个格子总共可选的路径数目,考虑到第一行和第一列的方向f[0][j]、f[i][0]的值都是1,只能向右、向下移动。第f[i][j]个格子的递推公式为:f[i][j] = f[i-1][j]+f[i][j-1],考虑一下两个步骤:
- 边界条件:第一行和第一列的方向f[0][j]、f[i][0]的值都是1:f[0][j]=1,f[i][0]=1
- 到达第f[i][j]个格子的路径数目是f[i-1][j]+f[i][j-1],也就是它的上方格子与左边格子的路径数目之和:f[i][j] = f[i-1][j]+f[i][j-1]
class Solution {
public int uniquePaths(int m, int n) {
int[][] f = new int[m][n];
for(int i=0; i<m;i++){
f[i][0] = 1;
}
for(int i=0; i<n; i++){
f[0][i]=1;
}
for(int i=1; i<m; i++){
for(int j=1; j<n; j++){
f[i][j] = f[i-1][j] + f[i][j-1];
}
}
return f[m-1][n-1];
}
}【四】最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
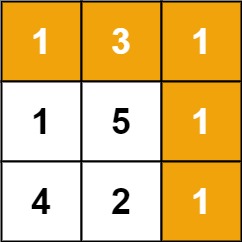
输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]] 输出:12
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 100
【解答】:此题与上面体2“机器人”类似,路径只能是向下或向右,因此网格的第一行和第一列的路径和是它前面格子累加。
对于不在第一行和第一列的格子,可以从它的上方或者左方分别移动一格到达,元素的最小路径和等于它的上方相邻元素与其左方相邻元素两者对应的最小路径和中的最小值加上当前元素的值。
创建二维数组 dp\textit{dp}dp,与原始网格的大小相同,dp[i][j]\textit{dp}[i][j]dp[i][j] 表示从左上角出发到 (i,j)(i,j)(i,j) 位置的最小路径和。显然,dp[0][0]=grid[0][0]\textit{dp}[0][0]=\textit{grid}[0][0]dp[0][0]=grid[0][0]。对于 dp\textit{dp}dp 中的其余元素,通过以下状态转移方程计算元素值。
当 i>0 且 j=0 时,dp[i][0]=dp[i−1][0]+grid[i][0]。
当 i=0 且 j>0 时,dp[0][j]=dp[0][j−1]+grid[0][j]。
当 i>0 且 j>0 时,dp[i][j]=min(dp[i−1][j],dp[i][j−1])+grid[i][j]。
最后得到 dp[m−1][n−1] 的值即为从网格左上角到网格右下角的最小路径和。
class Solution {
public int minPathSum(int[][] grid) {
if(grid == null || grid.length ==0 || grid[0].length == 0){
return 0;
}
int m = grid.length;//行大小
int n = grid[0].length;//列大小
int[][] dp = new int[m][n];
dp[0][0] = grid[0][0];
for(int i=1; i<m;i++){//求第一列的递推和
dp[i][0] = dp[i-1][0] + grid[i][0];
}
for(int i=1; i<n; i++){
dp[0][i]= dp[0][i-1] + grid[0][i];
}
for(int i=1; i<m; i++){
for(int j=1; j<n; j++){
dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1]) +grid[i][j];//到达第i行第j列元素的路径和最小值为第i-1行j列,i行j-1列的路径两者中较小者,加上第i行第j列的元素的值
}
}
return dp[dp.length-1][dp[0].length-1];//返回路径和数组中最后的那个就是所求的到达右下角路径的最小路劲和
}
}【五】零钱兑换
【题目】:给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11 输出:3 解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3 输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
【题解】:自下而上的方式进行思考,定义F(i)F(i)F(i) 为组成金额 iii 所需最少的硬币数量,假设在计算 F(i)F(i)F(i) 之前,我们已经计算出 F(0)−F(i−1)F(0)-F(i-1)F(0)−F(i−1) 的答案。 则 F(i)F(i)F(i) 对应的转移方程应为
F(i)=min(0…n−1)F(i−cj)+1
其中cj代表的是第j枚硬币的面值,即我们枚举最后一枚硬币面额是cj,那么需要从 i−cj这个金额的状态 F(i−cj)转移过来,再算上枚举的这枚硬币数量1的贡献,由于要硬币数量最少,所以F(i)为前面能转移过来的状态的最小值加上枚举的硬币数量1。
coins = [1, 2, 3], amount = 6
递推公式计算步骤为:
F(3) =min(F(3−c 1),F(3−c 2),F(3−c 3))+1
=min(F(3−1),F(3−2),F(3−3))+1
=min(F(2),F(1),F(0))+1
=min(1,1,0)+1
=1
代码如下:
public class Solution {
public int coinChange(int[] coins, int amount) {
int max = amount + 1;
int[] dp = new int[amount + 1];
Arrays.fill(dp, max);
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
for (int j = 0; j < coins.length; j++) {
if (coins[j] <= i) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
}【二】总结
动态规划的题目核心思想是找出递推公式,通常得的思想是:要求得第i个元素(步骤)的结果,先求得第i-1个或i-2个元素的结果,通常有f(i)=f(i-1)+f(i)或f(i-1)+f(i-2)之类的递推公式,具体结合题目的场景分析找出递推步骤和公式。其中要注意边界条件,通常是第一个、第一行、第一列之类的元素的值是不变的,可以作为递推的基础边界条件引入。最后通常是依次遍历或循环计算出结果集合的值即可。
我是程序大视界,坚持原创技术博客分享。
注:如果本篇博客有任何纰漏和建议,欢迎私信或评论留言!
文章持续更新,可以VX搜索「 程序大视界 」第一时间阅读,回复【资料】免费领取学习资料,添加博主VX好友,进群交流获取大厂面试完整考点,欢迎Star。