1. 题目链接:面试题 17.16. 按摩师
2. 题目描述:
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
**注意:**本题相对原题稍作改动
示例 1:
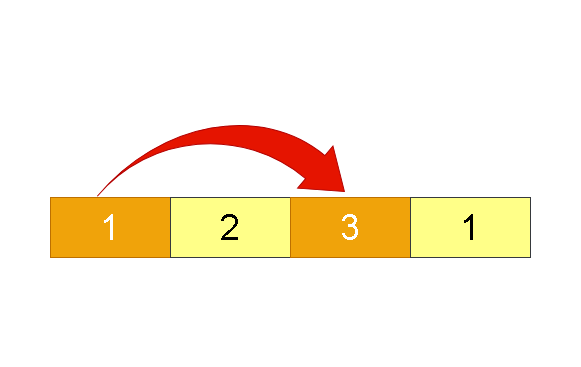
输入: [1,2,3,1] 输出: 4 解释: 选择 1 号预约和 3 号预约,总时长 = 1 + 3 = 4。示例 2:
输入: [2,7,9,3,1] 输出: 12 解释: 选择 1 号预约、 3 号预约和 5 号预约,总时长 = 2 + 9 + 1 = 12。示例 3:
输入: [2,1,4,5,3,1,1,3] 输出: 12 解释: 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约,总时长 = 2 + 4 + 3 + 3 = 12。
3. 解法(动态规划)
3.1 算法思路:
3.1.1 状态表示:
f[i]表示:选择到i位置时,nums[i]必选,此时的最长预约时长

g[i]表示:选择到i位置时,nums[i]不选,此时的最长预约时长
3.1.2 状态转移方程:
对于 f[i]:
如果nums[i]必选,那么我们仅需知道 i-1位置在不选的情况下的最长预约时长,然后加上nums[i]即可,因此f[i]=g[i-1]+nums[i]
对于 g[i]:
如果nums[i]不选,那么i-1位置上选或者不选都可以。因此,我们需要知道i-1位置上选或者不选两种情况下的最长时长,因此g[i]=max(f[i-1],g[i-1])
3.1.3 初始化:
f[0]=nums[0],g[0]=0
3.1.4 填表顺序:
根据状态转移方程,得从左往右,两个表一起填
3.1.5 返回值:
返回 max(f[n-1],g[n-1])
3.2 C++算法代码:
class Solution {
public:
int massage(vector<int>& nums) {
int n=nums.size();
if(n==0) return 0;//处理边界条件
//创建一个dp表
vector<int>f(n);
auto g=f;
//初始化
f[0]=nums[0];
//填表
for(int i=1;i<n;i++)
{
f[i]=g[i-1]+nums[i];
g[i]=max(f[i-1],g[i-1]);
}
//返回值
return max(f[n-1],g[n-1]);
}
};