Hi, 你好。我是茶桁。
逻辑回归预测心脏病
在本节课开始呢,我给大家一份逻辑回归的练习,利用下面这个数据集做了一次逻辑回归预测心脏病的练习。
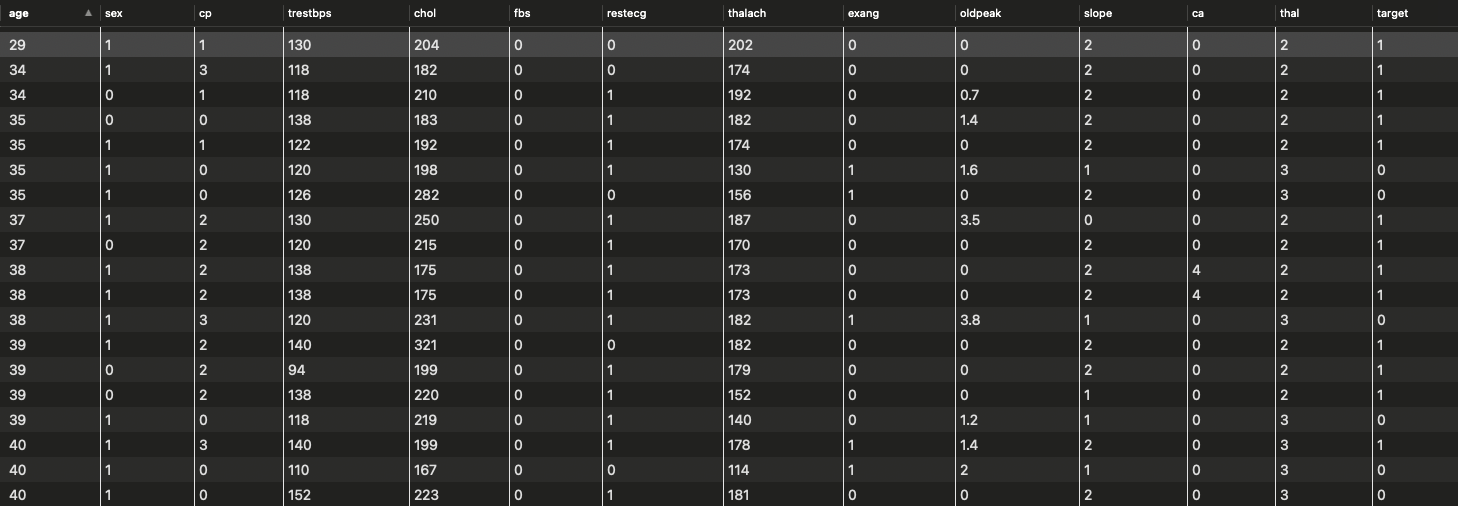
本次练习的代码在「茶桁的AI秘籍」在Github上的代码库内,数据集的获取在文末。这样做是因为我的数据集都是和百度盘同步的,很多数据集过大了,所以也就不传Github了。而且,我直接获取盘内同步数据也更方便。
还有一个原因,有些数据集可能以后会收费获取。
好,让我们进入今天的正课。
因为未来几节课的内容比较多。「核心基础」的这部分内容已经超出我原本的预计,咱们「核心基础」的部分刚刚过半,可是已经写到15节了,本来这部分内容我是想在21节左右结束的,所以,我们还是要压缩一下内容了。
这节课咱们还是继续讲解经典的机器学习。
支持向量机
接下来,要讲解一个非常有趣的方法:支持向量机。
支持向量机的原理其实可以很复杂,但它是一个很经典的思想方法。咱们就把它的核心思想讲明白就行了。其实我们平时在工作中用的也比较少。但是面试中有一些老一代的面试官会比较喜欢问这个问题。
支持向量机的核心思想,假如我们有两堆数据,希望找一根线去把它做分类,那么咱们找哪一根线呢?
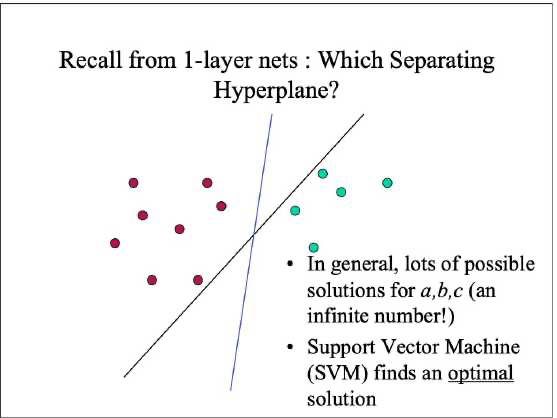
上图中,我们假设黑色的那根线定义为l,把离这根线最近的点,也就是直线距离最小的点,找到两个这样的点定义为P1、P2。
现在我们是希望离这个l最近的点,假如说是d1,d2,那么我们希望这两个距离加起来最大:max|d1+d2|。
现在再定义蓝色的线为直线b,那直线b做分类就比直线l要好。为什么直线b就比是直线l好呢? 因为直线b离d1,d2普遍都比较远。
现在这里的演示是一个二维平面中用一根线来分割,如果是在多维空间中,SVM的目标就是找到一个最佳的超平面来最大化间隔,同时确保正确分类样本。
假设我们有一组训练样本,每个样本用特征向量x表示,并且标记为正类别+1或负类别-1。
我们可以表示为以下凸优化问题:
m i n w , b 1 2 ∣ ∣ w ∣ ∣ 2 \begin{align*} min_{w, b}\frac{1}{2}||w||^2 \end{align*} minw,b21∣∣w∣∣2
其中对所有样本
y i ( w ⋅ x i + b ) ≥ 1 y_i(w \cdot x_i+b) \ge 1 yi(w⋅xi+b)≥1
w是超平面的法向量,b是截距项,yi是样本xi的标签,也就是+1或者-1。
为了解决这个优化问题,我们引入拉格朗日乘子 a i a_i ai来得到拉格朗日函数:
L ( w , b , a ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 N a i [ y i ( w ⋅ x i + b ) − 1 ] L(w,b,a) = \frac{1}{2}||w||^2 - \sum_{i=1}^Na_i[y_i(w\cdot x_i +b) - 1] L(w,b,a)=21∣∣w∣∣2−i=1∑Nai[yi(w⋅xi+b)−1]
然后我们要最小化拉格朗日函数,首先对w和b求偏导数,令它们等于0,然后代入拉格朗日乘子条件:
a i [ y i ( w ⋅ x i + b ) − 1 ] = 0 a_i[y_i(w\cdot x_i + b)-1] = 0 ai[yi(w⋅xi+b)−1]=0
然后我们就可以得到如下这个式子
w = ∑ i = 1 N a i y i x i s u m i = 1 N a i y i = 0 w = \sum_{i=1}^Na_iy_ix_i \\ sum_{i=1}^N a_iy_i = 0 w=i=1∑Naiyixisumi=1Naiyi=0
使用某种优化算法(例如,SMO算法),求解拉格朗日乘子 a i a_i ai。我们就可以使用求解得到的 a i a_i ai计算超平面参数w和b。
对于新样本x,使用超平面 w ⋅ x + b w\cdot x + b w⋅x+b的符号来预测其类别。
那我们讲了这么半天,都是一个支持向量机的数学演示过程,下面我们来看看具体的代码实现。
我们先来生成两组数据,这两组数据咱们让他距离更大:
import numpy as np
label_a = np.random.normal(6, 2, size=(50, 2))
label_b = np.random.normal(-6, 2, size=(50, 2))
我们现在来观察以下生成的这些点:
import matplotlib.pyplot as plt
plt.scatter(*zip(*label_a))
plt.scatter(*zip(*label_b))
plt.show()
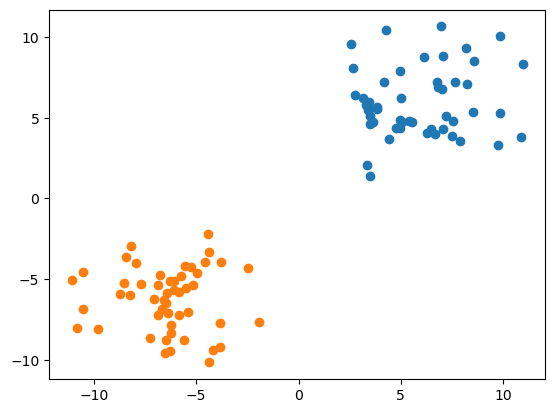
然后我们继续:
label_a_x = label_a[:, 0]
label_b_x = label_b[:, 0]
我们就将这两组数据的第一列分别取出来了。
接着我们随机的定义一些w和b
for i in range(100):
w, b = (np.random.random(size=(1, 2)) * 10 - 5)[0]
然后我们按照之前讲的数学演示来定义一个函数
def f(x):
return w*x+b
然后我们之前从数学演示里已经知道, y i ( w ⋅ x + b ) ≥ 1 y_i(w\cdot x+b) \ge 1 yi(w⋅x+b)≥1, 而我们也知道这个说的是距离,也就是说,同样的$y_i(w\cdot x+b) \le -1 $。
也就是说,我们要让函数f小于等于-1,并且大于等于1。当然,为了保证其被分到两边,我们将函数的最大值定义为小于等于-1, 将函数的最小值定义为大于等于1。这样就保证(-1,1)之间是不存在任何函数值:
np.max(f(label_a_x, w, b)) <= -1 and np.min(f(label_b_x, w, b)) >= 1
只有同时满足这两个条件的值,我们才会留下来进行保存。我们可以定义一个变量将其保存
w_and_b = []
for i in range(100):
w, b = (np.random.random(size=(1, 2)) * 10 - 5)[0]
if np.min(f(label_a_x, w, b)) >= -1 and np.min(f(label_b_x, w, b)) >= 1:
w_and_b.append((w, b))
在得到这些w,b之后,我们将这些w,b连起来进行画图:
for w, b in w_and_b:
x = np.concatenate((label_a_x, label_b_x))
plt.plot(x, f(x, w, b))
plt.show()
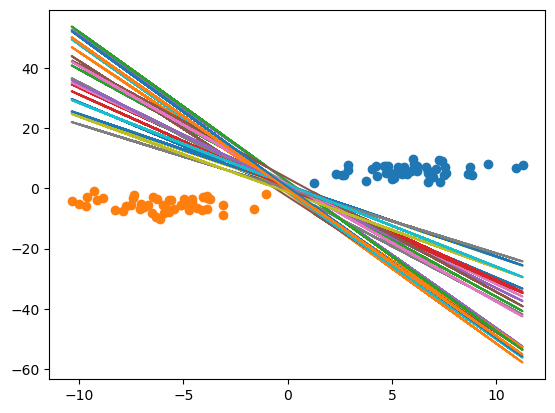
这样,我们就拟合出来了很多的曲线。这些个曲线到底哪一个是最好的那一个呢?
现在根据刚刚得到的那个结论,现在所有的 y i ( w ⋅ x i + b ) y_i(w\cdot x_i + b) yi(w⋅xi+b), 那么现在其实就是 m a r g i n = 2 ∣ ∣ w ∣ ∣ margin = \frac{2}{||w||} margin=∣∣w∣∣2。
那我们现在就找这个w最小的这个值就可以了。
w, b = min(w_and_b, key = lambda w_b: w_b[0])
all_x = np.concatenate((label_a_x, label_b_x))
plt.plot(all_x, f(all_x, w, b), 'r-o')
plt.show()
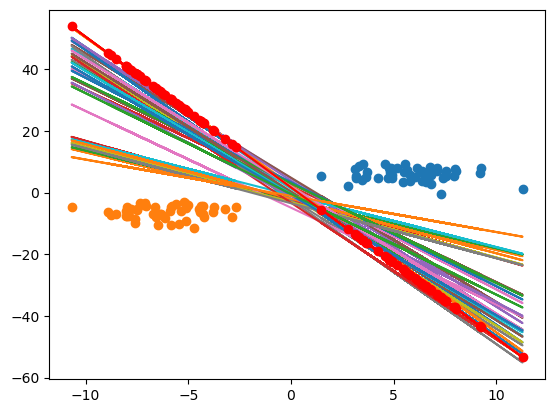
现在我们就可以看到那个最优的直线了,就是众多红色的点连接起来的那根线。
当然,最后代码执行顺序和讲解顺序有一些不一样,为了避免数据每次重新生成造成的差别,所以最开始是生成数据,之后是定义函数、过滤参数以及生成图像。
这个就是支持向量机的原理,我们找到离它所有的点的一个距离,让它这个边距最大,最后得到一个简化结果。
核函数
然后我们再来看另外一个点:「核函数」:
核函数是支持向量机里面非常重要的一个东西。
如果支持向量机只要数据是线性可分的,那么我们一定能够找到它的分割线。但是在实际的现实生活中有很多点并不是线性可分的。
举个例子,我们来画一张图:
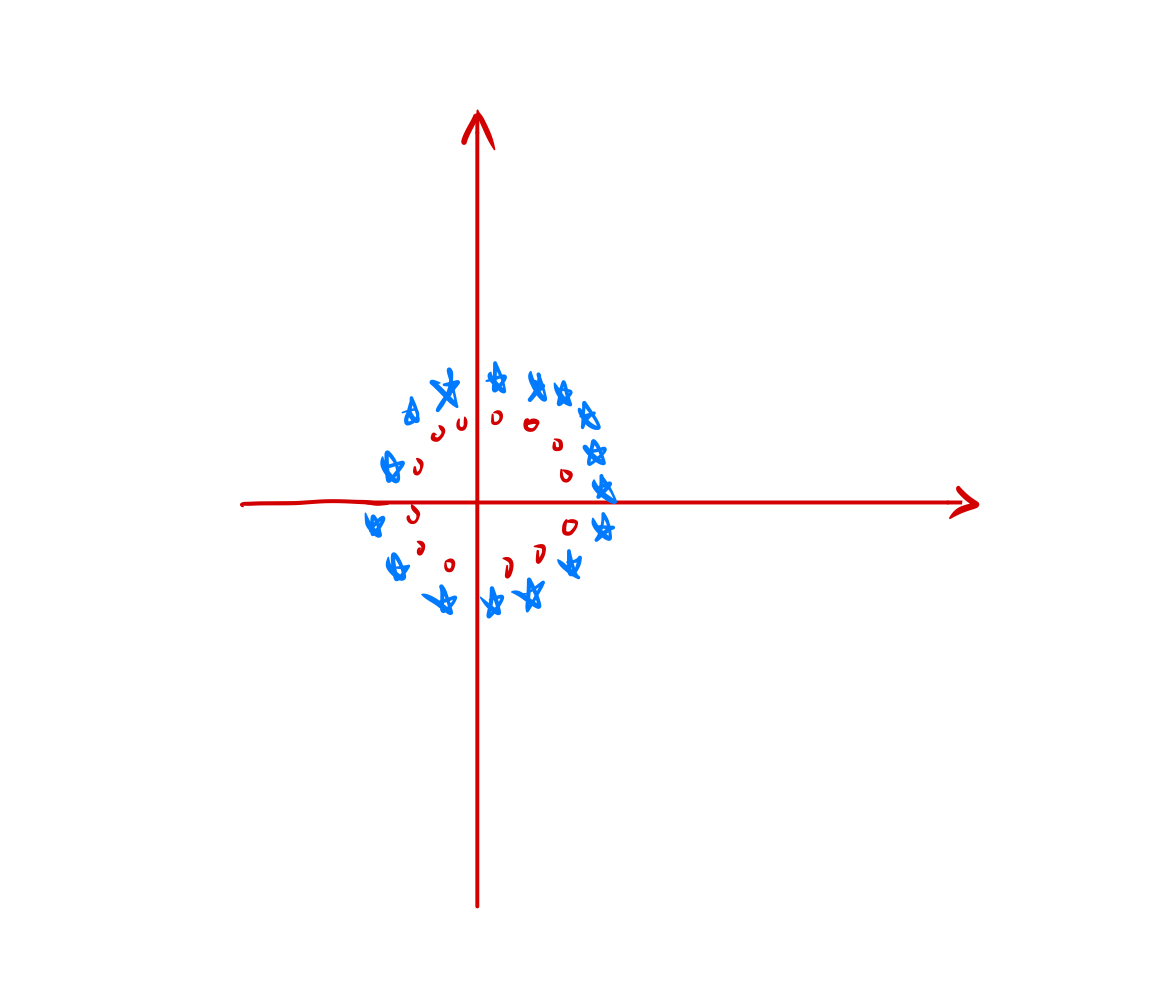
就比如图中的这种数据,是无论如何用一条直线无法分割的,不管怎么画,都无法把蓝色和红色的点分割开。
就像我们下面这张图:
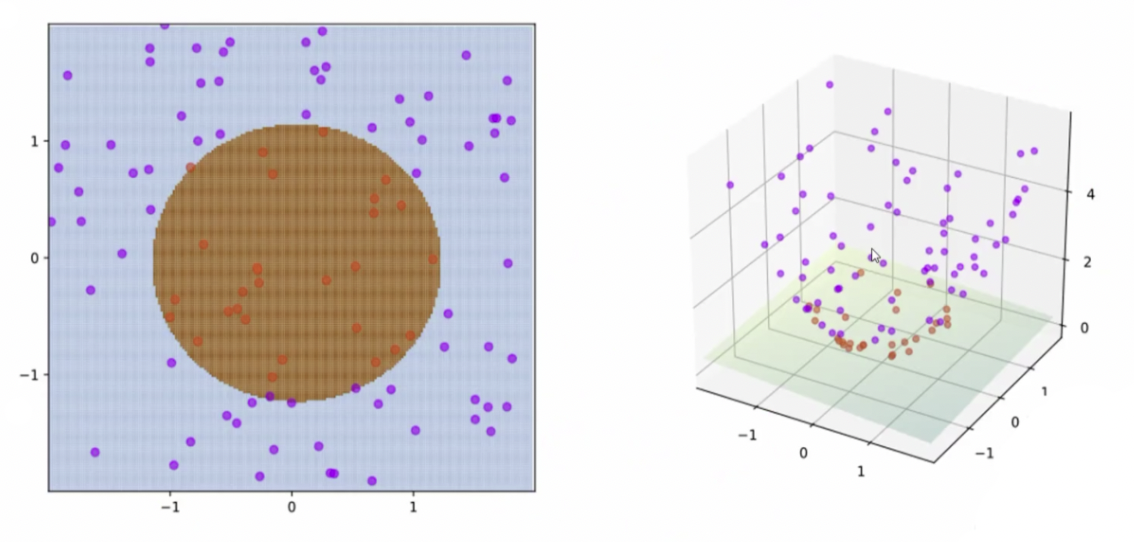
但是,我们我们可以做这样一件事情,假设我们在一个坐标轴上拥有8个点,A、B、C、D为一组,a,b,c,d为一组。如下图:
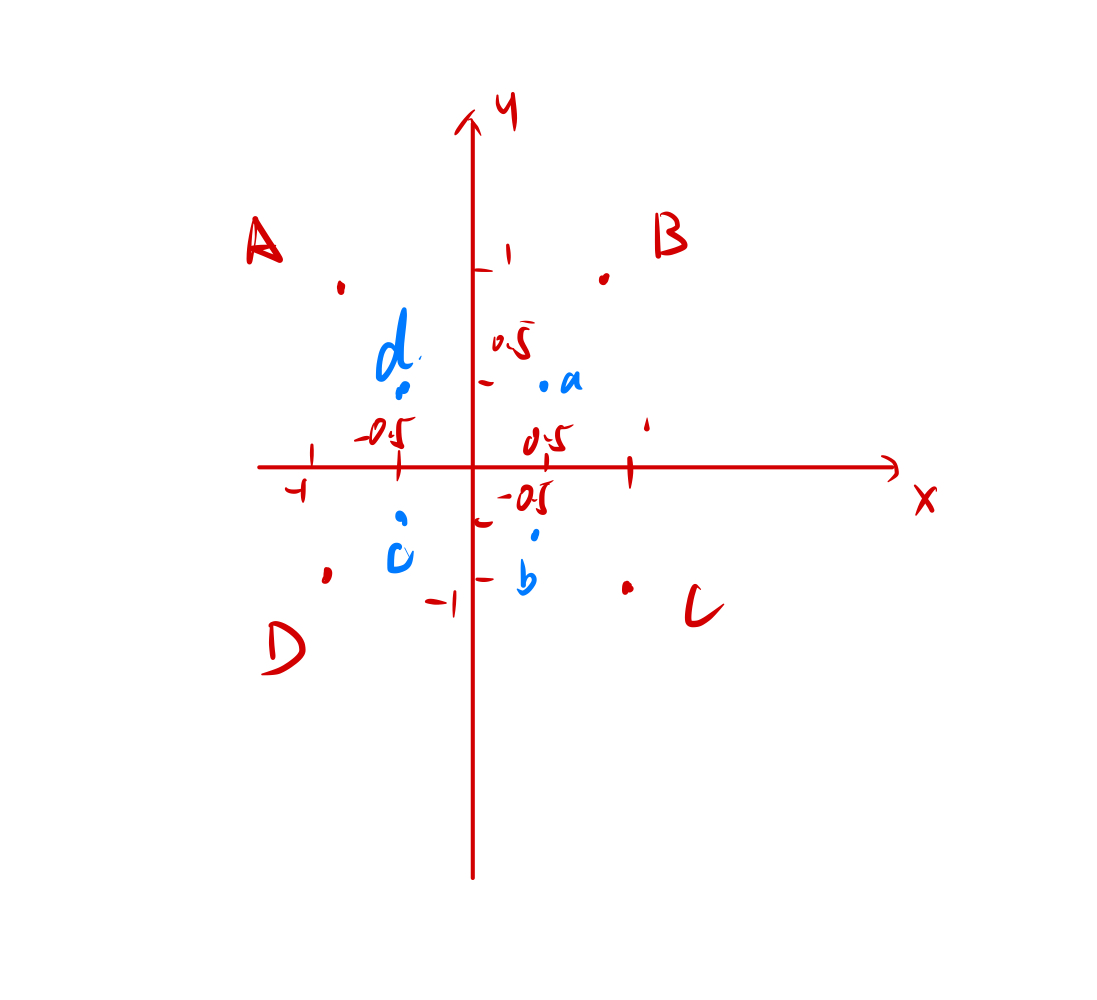
分别为A(-1,1), B(1,1), C(1, -1), D(-1,-1); a(-0.5, 0.5), b(0.5, 0.5), c(0.5, -0.5), d(-0.5, -0.5)。
现在我们ABCD和abcd是无法用一根直线来分割的,然后我们令:
f ( x ) = > { x 2 y 2 } \begin{align*} f(x) => \begin{Bmatrix} x^2 \\ y^2 \end{Bmatrix} \end{align*} f(x)=>{x2y2}
那在这种情况下,八个点分别就变成了A(1, 1),B(1, 1),C(1, 1),D(1, 1), a(0.25, 0.25),b(0.25, 0.25),c(0.25, 0.25),d(0.25, 0.25)。
那这样的情况下,我们就完全可以用一根直线去分割了:
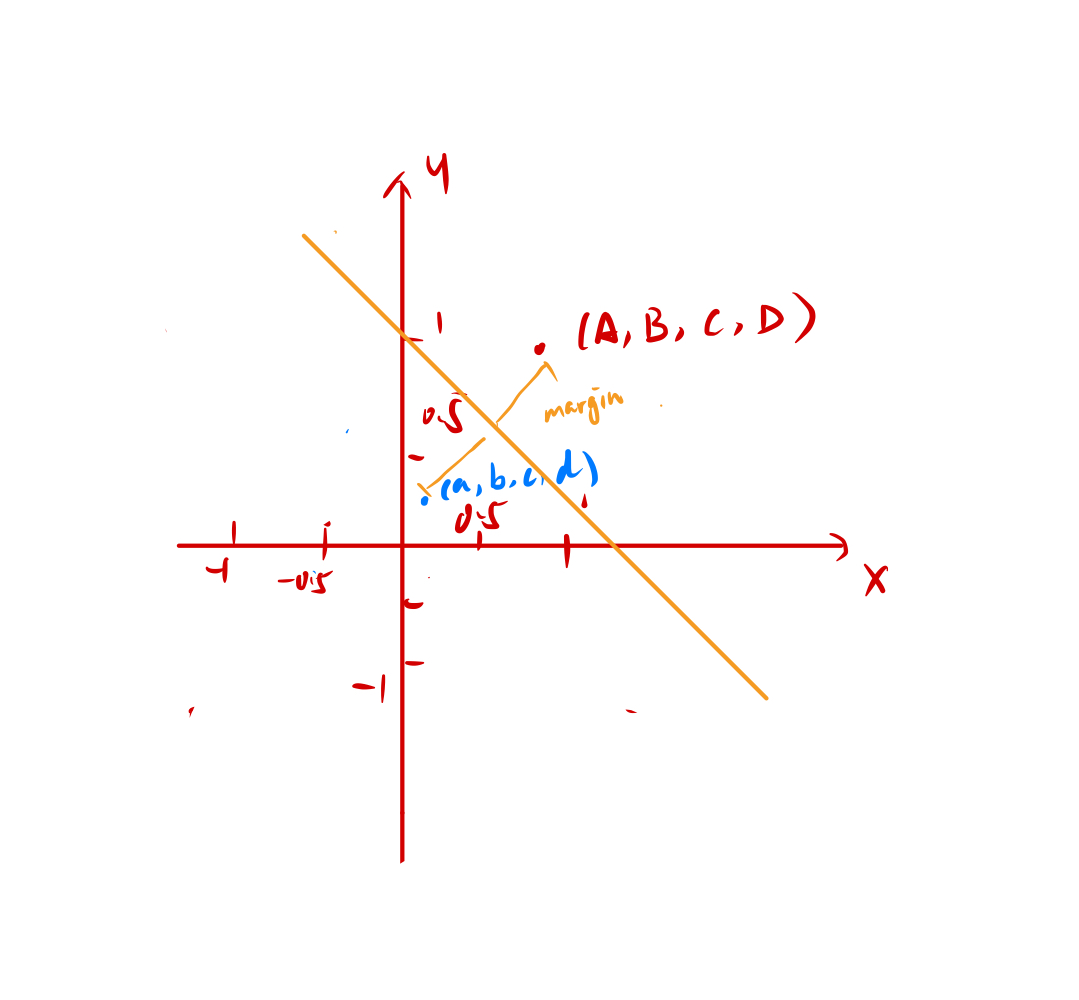
那现在找到这根线是w2 = wx+b,那我们遇到新数据应用到这个函数里边,再应用到这个线里面做分割就可以了。我们把原本线性不可分的东西,变成线性可分的。那么这个就是核函数神奇的地方。
支持向量机通过某非线性变换 φ(x) ,将输入空间映射到高维特征空间。特征空间的维数可能非常高。如果支持向量机的求解只用到内积运算,而在低维输入空间又存在某个函数 K(x, x′) ,它恰好等于在高维空间中这个内积,即K(x, x′) =φ(x)⋅φ(x’) ; 。那么支持向量机就不用计算复杂的非线性变换,而由这个函数K(x, x′) 直接得到非线性变换的内积,使大大简化了计算。我们就将这种函数函数 K(x, x′) 称为核函数。
φ ( x ) = [ x x 2 x 3 ] \varphi (x) = \begin{bmatrix} x \\ x^2 \\ x^3 \end{bmatrix} φ(x)= xx2x3
那其实,就类似的事情,已经有人总结了一些相应的公式来使用:
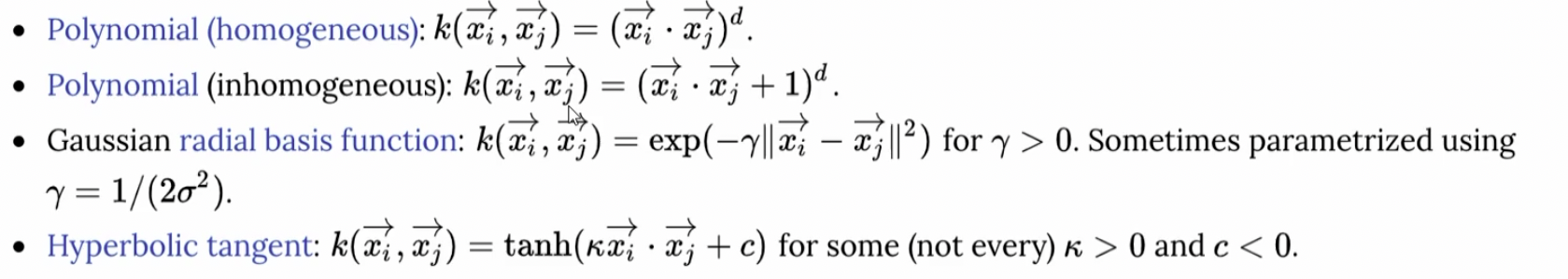
这些是一些常见的核函数。
一般在使用的时候调用它就可以,如果在用SVM的时候,它会有一个参数。可以自己定义一个核函数,但一般不自己定义,调用现有的就够了。
SVM其实也有弊端,当数据量很复杂的时候,现有的核函数就没有作用了。因为它会失效,所以我们需要很多的人工分析,整个效率很低。
但是在整个机器学习的发展史上,它曾经有非常重要的一段历史。有一段时间它的论文量非常的多,做科研的非常爱做SVM,不是因为快速,是因为可以提出来各种各样的Kerno函数。
假如有一组数据不好分割,但是你提出了一种新的核函数,这个函数量可以比较复杂啊
然后提升了分割率,提高了效果。
但是这种方法其实曾经一度让机器学习非常不受人待见,在学术圈非常不受人待见。搞机器学习的人就是每天就是发论文,说我的曲线比你的曲线强,这就是他们干的事。
所以10年左右,做机器学习、做人工智能的人都不说自己是做机器学习,做人工智能的。都换个名字,说做文本挖掘等等。
SVM因为要做各种升维,当数据量比较大的时候,计算量非常的复杂,计算需求量非常的大。
但是SVM它有个好处,就是它比较直观,还有就是SVM对于不平衡的数据比较有用。
好,这节课我们就讲到这里,下一节课我们来看「决策树」。
链接: https://pan.baidu.com/s/1Rl8xkQG4c-XSjL6cB4B1XQ?pwd=e8wi 提取码: e8wi 复制这段内容后打开百度网盘手机App,操作更方便哦
–来自百度网盘超级会员v6的分享