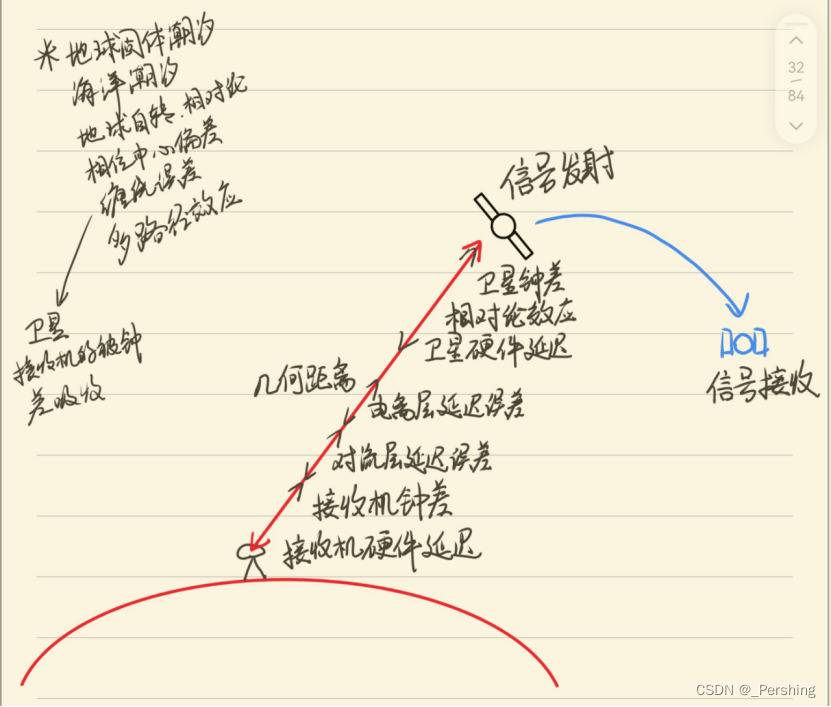
这是一篇发表在IEEE TRANSACTIONS ON INTELLIGENT TRANSPORTATION SYSTEMS上的论文，论文主要描述了一种刻画出行规律性的方法。

1.论文概述

论文主要描述了一种刻画出行规律性的方法。首先，论文给出了对出行活动序列（travel event）进行数学化描述的方法；在这之后，作者给出了基于出行活动序列的规律性度量方法。
对于作者所提出的这种规律性度量方法，他们认为最大的创新在于他们所提出的这种方法是calendar free的，这是什么意思呢？以前大家经常把regularity和periodicity在一定程度上画上等号，但是作者专门强调这两者是不同的。诚然，periodicity是一种regularity，但是regularity并不一定是periodicity的。举个例子，有个出行者有时候周五出城去郊游，然后周日回，有时候周六出城去郊游，然后周一回。这在日期表上不是periodicity的，但是他的行为展现出了一定的regularity。作者说他们提出的这个方法可以得到regularity，即calendar free。

2.方法论

2.1 出行活动序列的数学化表达

作者首先介绍了出行活动序列的数学化表达。首先把一个人的出行活动序列视作是一个随机过程$X_u$，这个随机过程生成一个活动，该活动是一个随机变量，用$X_u$来表示。$X_u$生成具体的活动$x$，其中$x\in E_u$，$E_u$就是随机变量$X_u$所有可能的集合。在这里，作者假设活动都是离散的，即使是连续的也可以通过一定的手段离散化，因此这个假设也是没问题的。这样一来，一个人的活动序列便可以表示为 X u = { . . . , X − 1 , X 0 , X 1 , X 2 , . . . } \pmb{X_u}=\{...,X_{-1},X_0,X_1,X_2,...\} Xu​={...,X−1​,X0​,X1​,X2​,...}。这个活动变量序列生成具体的活动也就是个体u的活动序列了。其中每个活动变量都会以一定的概率分布生成活动，该概率分布可以写成 p ( x ) = P r { X u = x } , x ∈ E u p(x)=Pr\{X_u=x\},x\in{E_u} p(x)=Pr{Xu​=x},x∈Eu​。
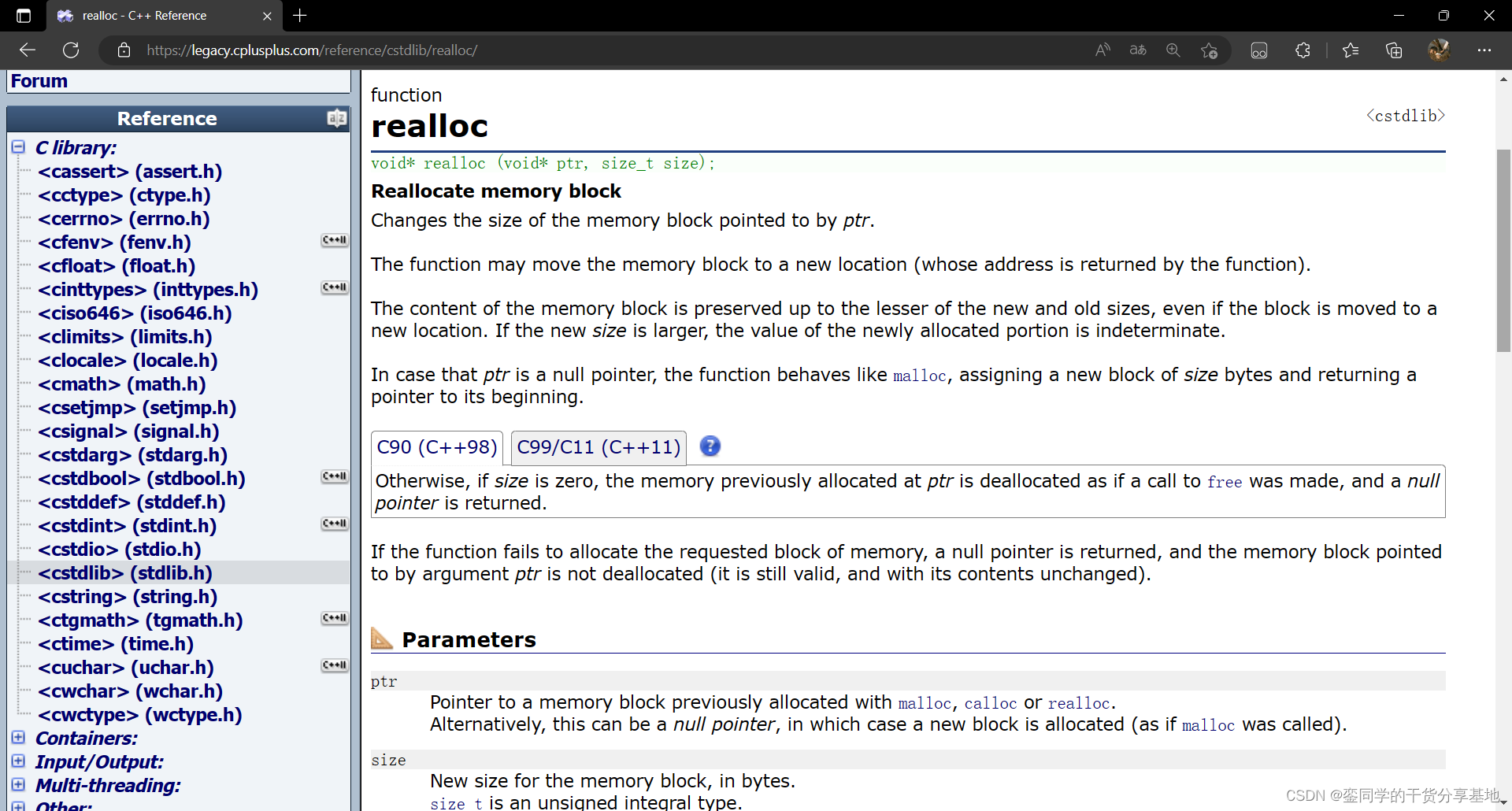
文章举了一个下图的实例，对于一个从家去工作，再去饭馆吃饭，再回家的人，他可以进行如下的序列化表达。不同的研究目标和不同的数据粒度，可以进行不同的序列化表达，下图给了一些示范。

2.2 regularity度量

文章给出了两种度量方式，第一种是用Entropy，第二种是用Entropy Rate，作者分别解释了两种不同度量手段区别，并进行了一些较深入的分析。
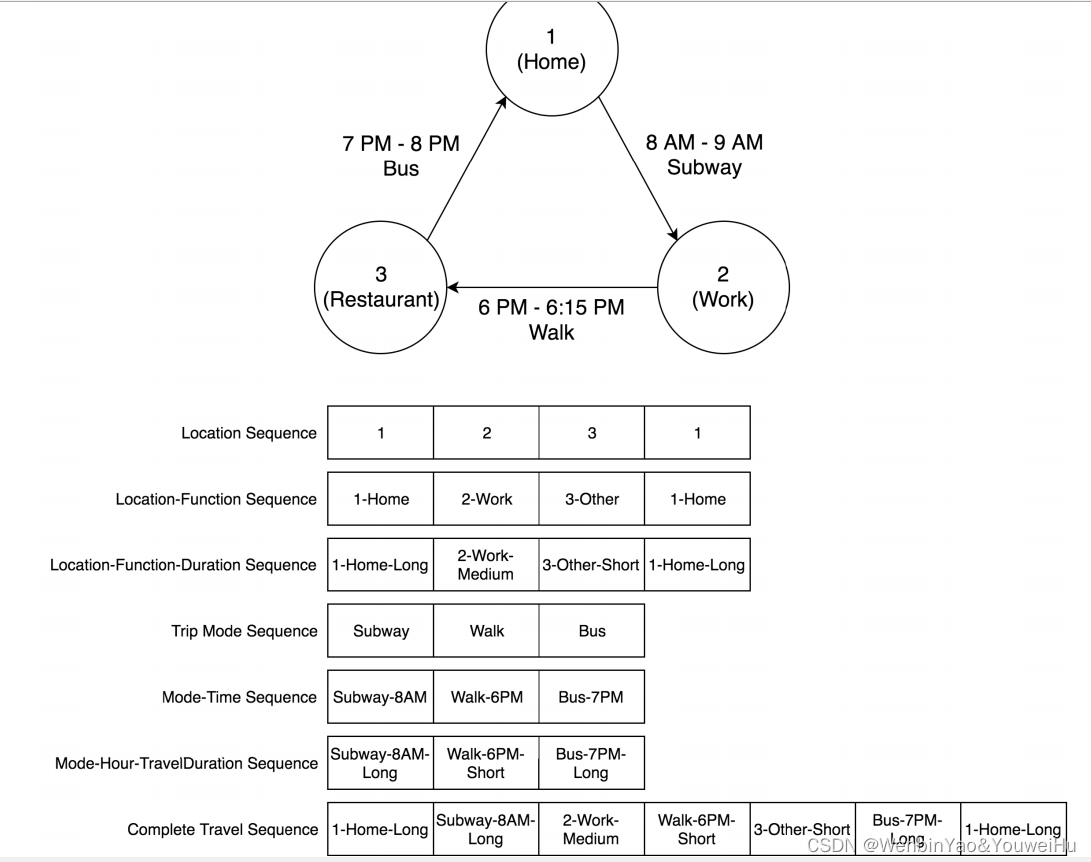
其中Entropy来度量的话是没有考虑顺序的，也就是活动序列的顺序实际上被忽略掉了，而只是考虑了活动的重复性，也就是说对于一个人是：家庭->上班->饭店->家庭，还是：家庭->饭店->上班->家庭，是没什么区别的，因为只是计算这个序列的Entropy而已。Entropy的计算可以通过下式进行。

而Entropy Rate则不同，Entropy Rate是考虑了序列的顺序的，其计算公式如下：

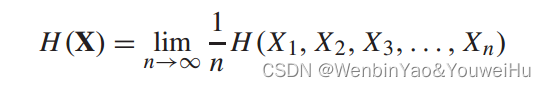
可以证明上式的计算可以被转化为：

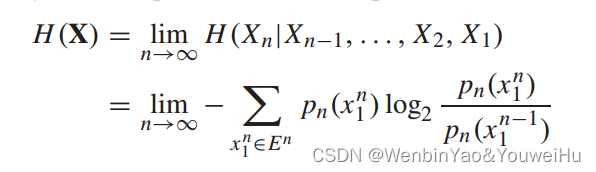
文章提到：entropy rate measures the average entropy of each new event generated
by random process X, accounting for preceding events.entropy rate计算得到的是一种考虑之前的活动的entropy的平均值。如果之前的活动可以完全确定后一个活动，那么entropy rate=0。因此也可以自然而然的想到对于同一个活动序列的entropy和entropy rate的差值就反应出了前面的活动与接下来将发生的活动的相关性。

2.3 entropy rate 的计算

作者提到 entropy rate的计算可以使用朴素暴力法，但是朴素暴力法对于较长的序列就不适用了。 entropy rate也可以用CTW、BWT、LZ等方法进行计算，作者最后使用了BWT算法来对entropy rate进行估算，文章还给了一个例子阐述BWT算法的原理。

3.实例分析

作者用长达一个月时间的公交IC卡数据分析了每个出行者的regularity，其实就是计算出每个人的entropy rate和entropy。
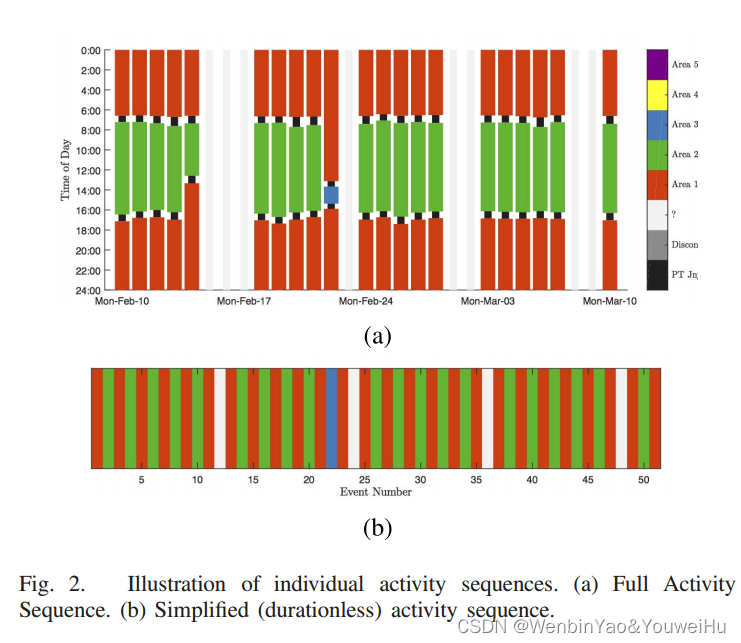
首先，自然是需要将出行者的出行活动序列进行序列化表达，如下图所示：图a是比较完整信息的出行序列，图b就是最终使用的出行序列，可见作者忽略掉了活动的duration。

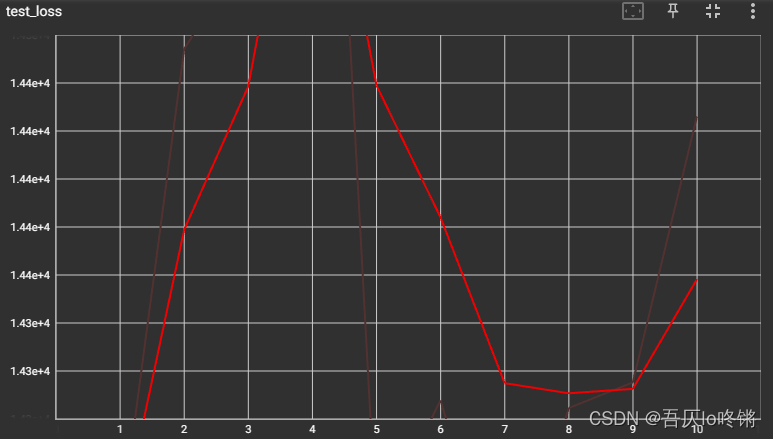
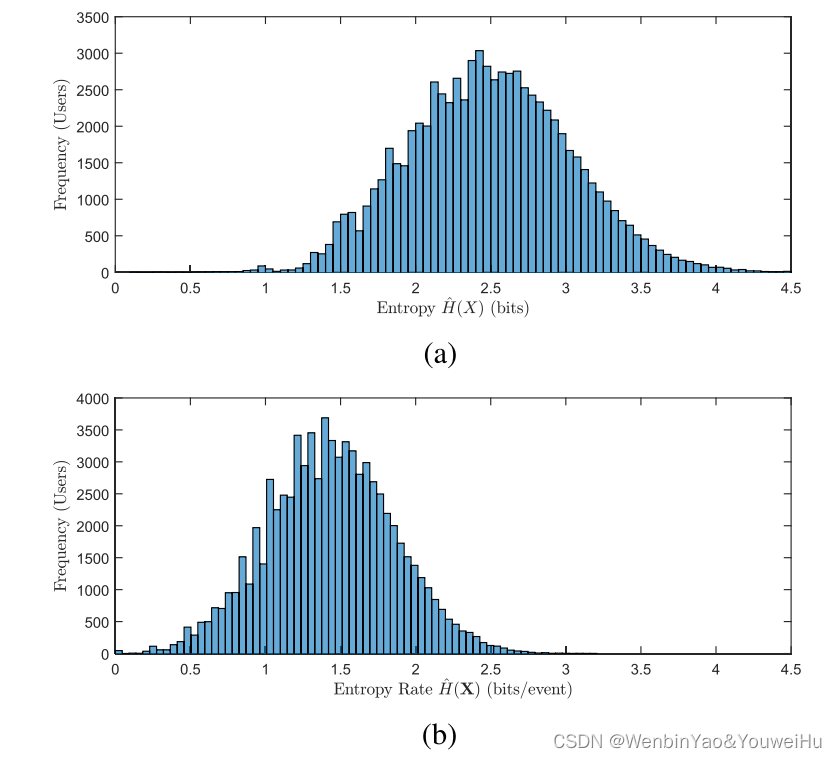
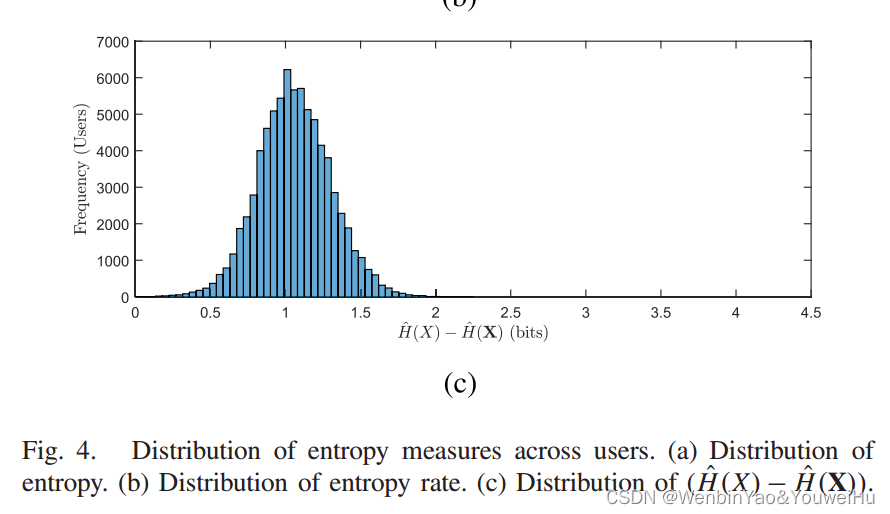
然后作者算出了每个出行者的entropy rate和entropy。结果分别如下两图所示。图c是两者的差，其大小其实就是反应了该出行者的行为的可预测性，越大，就代表可预测性越大，越接近0，说明可预测性越小。

参考文献

Goulet-Langlois, G. , Koutsopoulos, H. N. , Zhao, Z. , & Zhao, J. . (2018). Measuring regularity of individual travel patterns. IEEE Transactions on Intelligent Transportation Systems, 1583-1592.