翻看了一下记录,离上一次GNSS内容的更新已经过去9个月了。时间过的太快,硕士生涯已经过去一半,有遗憾也有收获,过去的9个月经历了各种喜怒哀乐以及迷茫。永远相信美好的事情即将发生,GO LONG CHINA!
今天写写GNSSS定位中的误差源,其实这个板块写的比较乱,一开始我只想记录一下自己的学习过程,但是总被各种事情打断,感觉还是需要写的稍有逻辑一些,这次从开头说起。
什么是定位
说起定位,显而易见的会想到确定位置,GNSS定位便是利用GNSS全球卫星导航系统这个技术来实现位置的确定这样一个过程。通俗点,定位其实就是一个建模解方程的过程,首先我们可以来构建几个简单的方程。设想在地球上,如果想知道我的位置,需要几颗卫星的数据?先考虑位置是什么,无论是相对位置还是绝对位置,无非是在不同的参考系下的点罢了,所以求位置其实就是求坐标。地球是一个三维物体,知道在地球上的位置即求在地球参考系下的(X,Y,Z)的三维坐标,很显然,三个未知数的求解需要三个方程(这里也可以这么想,知道与卫星的距离即以卫星为球心的一个球表面上的点,两个球确定一个圆,而三个球则可以确定两个点,再考虑到在地球上这个条件,就可以确定一个点。)。
假设知道卫星发射信号的时刻,接收到卫星信号的时刻,以及卫星传播的速度,即光速,那距离等于速度×时间,距离是卫星和我们在地球参考系下的坐标的平方和再开方。这样一个方程就出来了。求坐标的三个未知数就得三个卫星给出的三个方程,但实际上最少需要四个卫星,为什么呢?因为时间,坐标是一个时刻下的位置,假设我们得到的距离不是在一个时间下建立的方程,方程是求不出解的,对时间的要求是很精确的,而不同卫星记录下的时间可能是有微小的差异的,在光速的放大下,误差是不能够忽略的,因此我们要保证时间的同步性,这也是为什么卫星上要搭载原子钟的原因。所以实际上最少我们需要求解四个未知数(X,Y,Z,T)也就是最少需要接收到四个卫星的信号。这就是定位的本质,后面的各种思考都是对这个简单的模型进行缝缝补补,使其仍能满足在地球上受到各种误差下的条件亦或者是使得模型更加的精确,计算得到的位置坐标具有更小的误差和不确定性。
实际上,现在的定位通常需要上十颗卫星的参与,这样方程才能够解出卫星从发射信号到穿越大气层再到被接收机接受过程中的种种干扰误差导致的未知数,并且得到一个较为可靠的结果。搞清楚了这些,我们先来看看全球定位系统的组成。
全球定位系统
全球定位系统由三个部分组成:空间部分(卫星)、地面监控部分和用户部分。
- 空间部分不同的星座有不同的卫星设计,例如GPS由24颗中轨道卫星组成在6个轨道面运行,北斗三代则由24颗中轨道卫星、3颗静止轨道卫星和3颗倾斜同步轨道卫星共30颗卫星组成。
- 地面监控部分则负责支持整个系统的运行,由主控站,监测站,注入站和通信辅助系统组成。其中注入站负责在卫星飞临上空是给卫星上注信息。
- 用户部分以GPS接收机为例,天线单元由天线和前置放大器组成,缺少放大器会使得无法检测到微弱的信号产生的电流。在接受通道中,导航电文的每个bit持续时间约为20ms。
对于卫星发射的信号,则由载波、测距码和导航电文构成。其中载波是用来运载调制信号的高频震荡波,但反而是发现测距码的得到的精度不高,现在越来越多的使用载波的相位测量来进行,前者称为伪距,后者称为相位。导航电文中包含了卫星的轨道和一些基础的改正以及卫星的状态信息,构成了最重要的运输内容。
而利用导航电文中的广播星历信息计算卫星的位置,在上一篇(二)中已经介绍过了。
以上便是全球卫星导航系统的相关内容,基于此,接下来便可以讲讲定位中的误差源了。
GNSS定位中的误差源
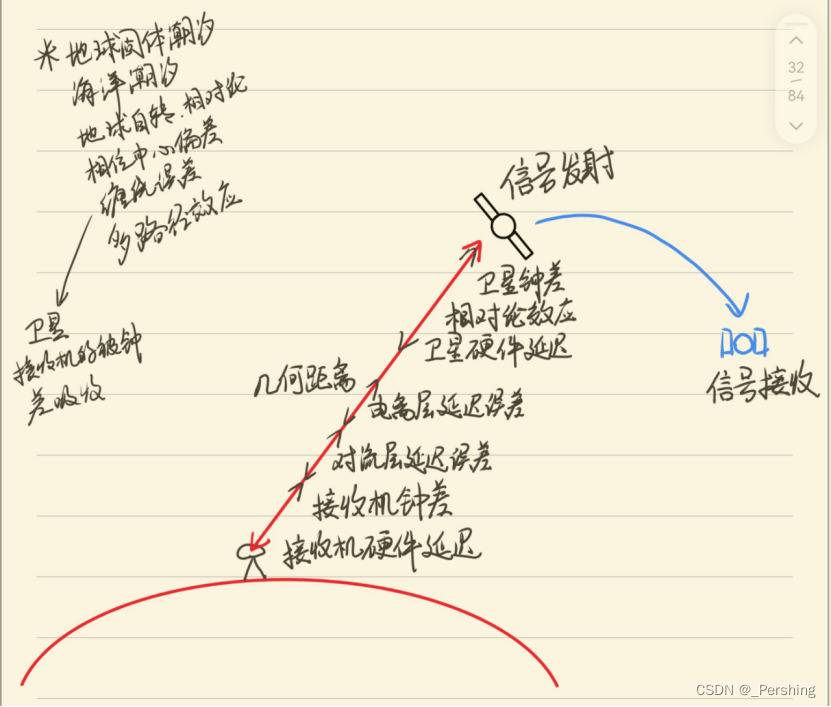
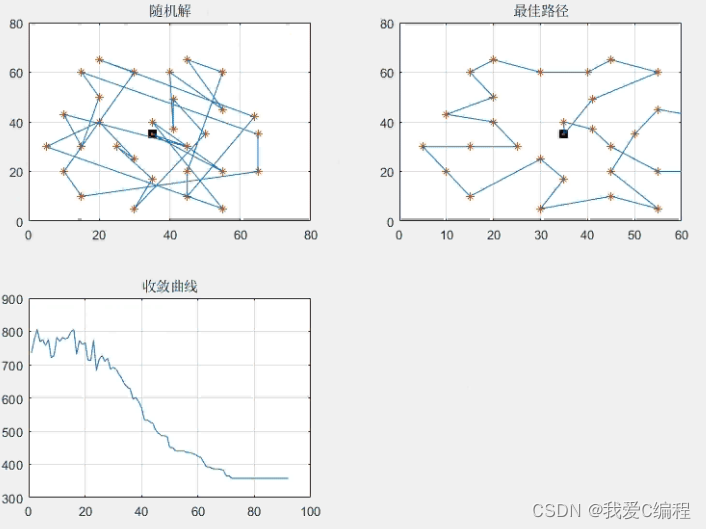
如图,从误差源来看大体可以分为三类:与卫星有关的误差,与信号传播有关的误差,与接收机有关的误差。
与卫星有关的误差
- 卫星星历误差,取决与卫星定规系统的质量
- 卫星钟钟误差,其中系统误差可以使用模型加以改正,随机误差只能用钟的稳定性表示统计特性
- 相对论效应,通常在卫星发射前对钟的调整会考虑到相对论
与信号传播有关的误差
- 电离层延迟,这是现在高精度定位中影响最大也是极需解决的误差,随着11年一个的太阳活动周期的轮回,现如今我们处于太阳活动上升年,电离层的活跃势必会影响到定位的精度,有关电离层的改正在(一)中已做介绍。
- 对流层延迟,对流层是高度在50km以下的大气层,其延迟对伪距和载波相位的影响是相同的。
- 多路径效应,主要取决于测站周边的环境,天线的形式以及观测时间的长短。
与接收机有关的误差
- 接收机钟误差,会比卫星的更为显著
- 接收机的位置误差,在授时和定轨时,接收机的位置往往认为已知,其与真实坐标存在一定误差。
- 接收机的测量噪声,属于随机测量误差
误差处理策略
根据不同的误差特性,也有相应的一些处理策略:
1、使用精密产品,例如精密星历、精密钟差产品,电离层、对流层延迟产品,差分码偏差产品。
2、模型改正,适用于能被精确模型化的误差。
3、线性组合法,使用观测值线性组合可以削去误差。例如常见的无电离层组合,半和模型(几何距离不变)。
4、参数估计法,将误差作为新增一个参数放在模型里一同估计。