Day 13 python学习笔记

news2024/12/25 1:05:09

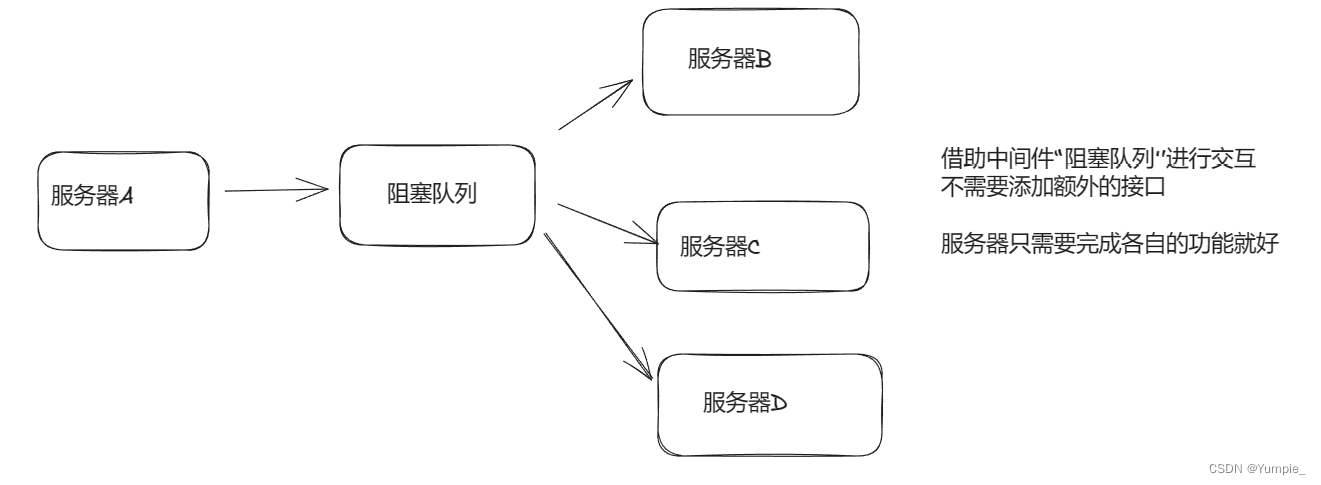
模块

内置模块

加密

加密是成本与时间的问题

不可逆加密

哈希加密，单向性，唯一性。

可逆加密

对称加密：加密与解密采用同一密匙（如文件压缩时设置密码） DES算法
非对称加密：采用一对密匙，公匙、私匙。RSA算法（复杂，CA认证）

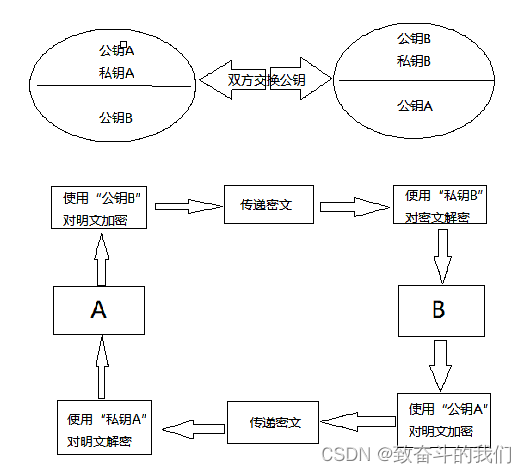
A 要向 B 发送信息，A 和 B 都要产生一对用于加密和解密的公钥和私钥。
A 的私钥保密，A 的公钥告诉 B；B 的私钥保密，B 的公钥告诉 A。
A 要给 B 发送信息时，A 用 B 的公钥加密信息，因为 A 知道 B 的公钥。
A 将这个消息发给 B (已经用 B 的公钥加密消息)。
B 收到这个消息后，B 用自己的私钥解密 A 的消息。其他所有收到这个报文的人都无法解密，因为只有 B 才有 B 的私钥。

hashlib模块

hashlib：提供标准的哈希加密算法（典型版本：MD5,sha256）

主要用于校验，不用于加密，因为过于标准，容易破解

hash.md5(以字节形式传入的数据)

hash.md5(以字节形式传入的数据) 将数据以MD5版本进行加密转换然后返回

扩展：" xxxx ".encode 将字符串转换为字节

>>> md5 = hashlib.md5("123456".encode())
>>> md5
<md5 _hashlib.HASH object @ 0x00000158299C3CD0>
>>>

hash.sha256(以字节形式传入的数据)

hash.sha256(以字节形式传入的数据) 将数据以sha256版本进行加密转换然后返回

>>> msg = hashlib.sha256("123456".encode())
>>> msg
<sha256 _hashlib.HASH object @ 0x0000015829ABAD30>

变量（经过MD5或sha256加密）.hexdigest( )

变量（经过MD5或sha256加密）.hexdigest( ) : 查看加密过的数据

>>> md5.hexdigest()
'e10adc3949ba59abbe56e057f20f883e'   #转化过就是'123456'
>>>
>>> msg.hexdigest()
'8d969eef6ecad3c29a3a629280e686cf0c3f5d5a86aff3ca12020c923adc6c92'
>>>                                   #转化过就是'123456'

可以在md5在线解密破解,md5解密加密 (cmd5.com)网站上查询

变量（经过MD5或sha256加密）.update(以字节形式传入的数据 )

变量（经过MD5加密）.update( 以字节形式传入的数据) 添加一些无关数据，使密文难以被破解（延值混淆）

>>> md5.update("789".encode())
>>> md5.hexdigest()
'25f9e794323b453885f5181f1b624d0b'

>>> md5.update("789lovelovelove".encode())
>>> md5.hexdigest()
'4771abe61779b74889663e246a7accba'

hmac模块

hash加密相关模块，为加密而设计。做哈希算法时，先进性对称加密，再转入哈希加密中去。密钥做两次加密。

hmac.new(延值混淆的数据，加密的数据，加密的版本)

hmac.new(延值混淆的数据，加密的数据，加密的版本)

进行两层加密：

第一次加密的数据用延值混淆的数据进行对称加密
将对称加密的结果用加密的版本再进行一次加密

如果是简单的延值混淆的数据，haslib模块就会被破解，但hmac难以破解

>>> abc = hmac.new("11".encode(),"123456".encode(),"md5")
>>> abc.hexdigest()
'e07639b66e869fe31a676398c283bb0e'
>>>

UUID模块

UUID 是通用唯一识别码（Universally Unique Identifier）的缩写，是一种软件建构的标准，亦为开放软件基金会组织在分布式计算环境领域的一部分。其目的，是让分布式系统中的所有元素，都能有唯一的辨识信息，而不需要通过中央控制端来做辨识信息的指定。如此一来，每个人都可以创建不与其它人冲突的UUID。在这样的情况下，就不需考虑数据库创建时的名称重复问题。最广泛应用的UUID，是微软公司的全局唯一标识符（GUID），而其他重要的应用，则有Linux ext2/ext3文件系统、LUKS加密分区、GNOME、KDE、Mac OS X等等。另外我们也可以在e2fsprogs包中的UUID库找到实现。

简单来说：就是一个标准，用于获得一个永远不会重复的序列

uuid.uuid4( )

uuid.uuid4( )：用于获得一个永远不会重复的序列

>>> uuid.uuid4()
UUID('2342e7e8-dce3-40ce-b89d-dccb13944621')
>>>

第三方模块

第三方模块：别人写的比较好用的模块（使用需要下载第三方模块）

pip模块

pip：windows有python环境就自带pip

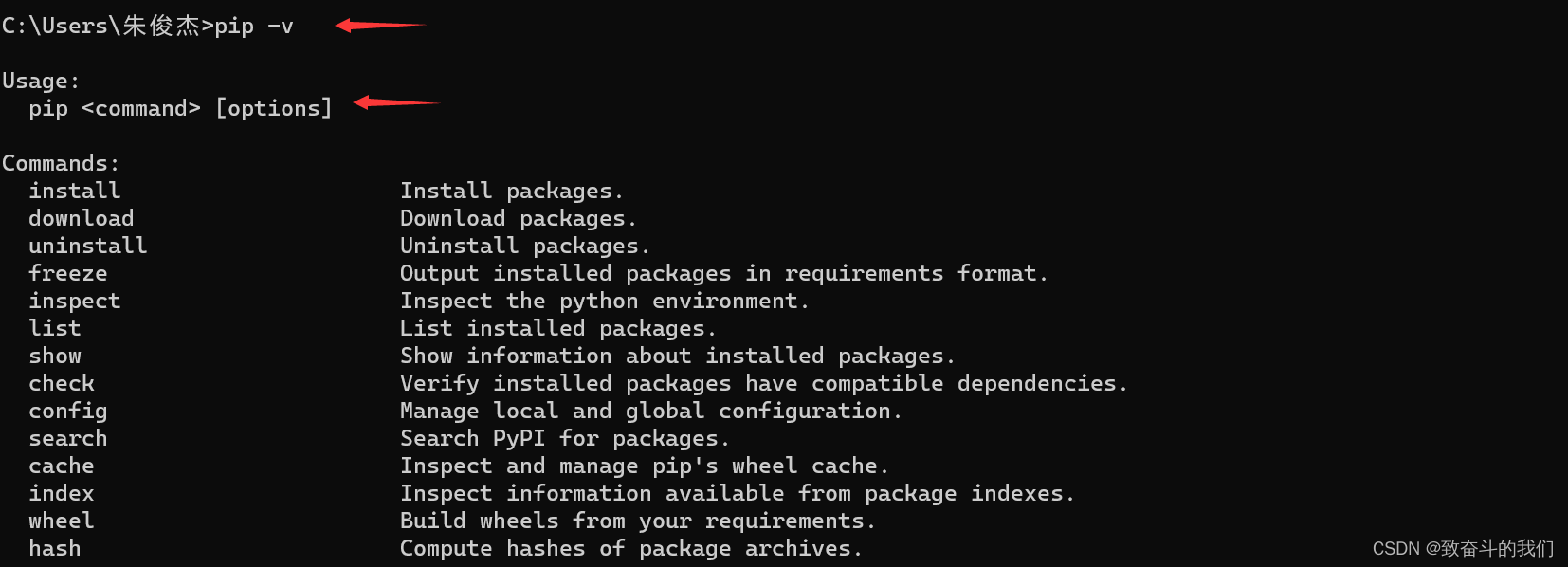
Linux系统则需要下载：

下载命令：yum install python3-pip

Ubuntu（乌邦图）系统也需要下载：

下载命令：apt install python3-pip

查询帮助文档命令：pip --help

pip install 包名

pip install 包名下载包

pip list

pip list 查看下载的列表（包）

C:\Users\朱俊杰>pip list
Package    Version
---------- -------
pip        22.2.2
setuptools 63.2.0

[notice] A new release of pip available: 22.2.2 -> 23.3.1
[notice] To update, run: python.exe -m pip install --upgrade pip

C:\Users\朱俊杰>