文章目录
- 概要
- 图像金字塔
- 轮廓:入门
概要
文章内容的概要:
平滑图像金字塔:
图像金字塔是什么?
图像金字塔是指将原始图像按照不同的分辨率进行多次缩小(下采样)得到的一系列图像。这种处理方式常用于图像处理中的多尺度分析。
高斯金字塔:
使用高斯滤波器进行图像的平滑操作,然后下采样得到不同分辨率的图像,构成高斯金字塔。
拉普拉斯金字塔:
拉普拉斯金字塔是由高斯金字塔图像和其高分辨率版本重建的图像差得到的,用于图像重建和图像增强。
轮廓:
轮廓检测基础:
介绍了轮廓检测的基本概念和OpenCV中相关函数的使用,包括cv2.findContours()函数。
轮廓特征:
讲解了如何提取轮廓的特征,例如轮廓面积、周长、重心等,并举例说明了如何在实际应用中使用这些特征。
轮廓近似:
探讨了轮廓近似的方法,包括使用Douglas-Peucker算法进行曲线近似,以及多边形逼近轮廓。
轮廓匹配:
讲解了如何使用轮廓匹配来识别和匹配目标对象,包括轮廓匹配的应用示例。
图像金字塔
使用图像金字塔去创造一个新的水果,“橘果(Orapple)”
函数:cv.pyrUp(), cv.pyrDown()
通常,我们处理图像时使用的是固定分辨率。然而,在某些情况下,我们需要在不同的分辨率下处理同一张图像。例如,在搜索图像中的某些内容(如面部)时,我们无法确定对象在图像中的实际大小。因此,我们需要创建一组具有不同分辨率的相同图像,并在这些图像中搜索对象。这种具有不同分辨率的图像集被称为图像金字塔。这个术语的来源是因为当这些图像以堆叠的形式存在时,最高分辨率的图像位于底部,而最低分辨率的图像位于顶部,形象地呈现出金字塔的形状。
图像金字塔主要有两种类型:高斯金字塔和拉普拉斯金字塔。
在高斯金字塔中,低分辨率图像(较高层级)通过去除高分辨率图像(较低层级)中的连续行和列而生成。接着,用低层级中的5个像素通过加权平均形成高层级中的1个像素,权重是符合高斯分布的。通过这种操作,原始图像的大小会缩小到原来的四分之一。然后,这个过程可以继续向上层级执行,分辨率就会逐渐减小,同时图像的面积也会相应减小。相反地,如果我们从低层级向高层级执行相反的操作,图像的分辨率会逐渐增加,同时图像的面积也会增大。在OpenCV中,我们可以使用cv.pyrDown()和cv.pyrUp()函数来构建高斯金字塔。
import cv2 as cv
img = cv.imread('messi5.jpg')
higher_reso = img # 最高分辨率图像
# 创建高斯金字塔(降采样)
lower_reso = cv.pyrDown(higher_reso)
以上代码中,cv.pyrDown()函数用于将higher_reso图像降低一级分辨率,结果存储在lower_reso中。
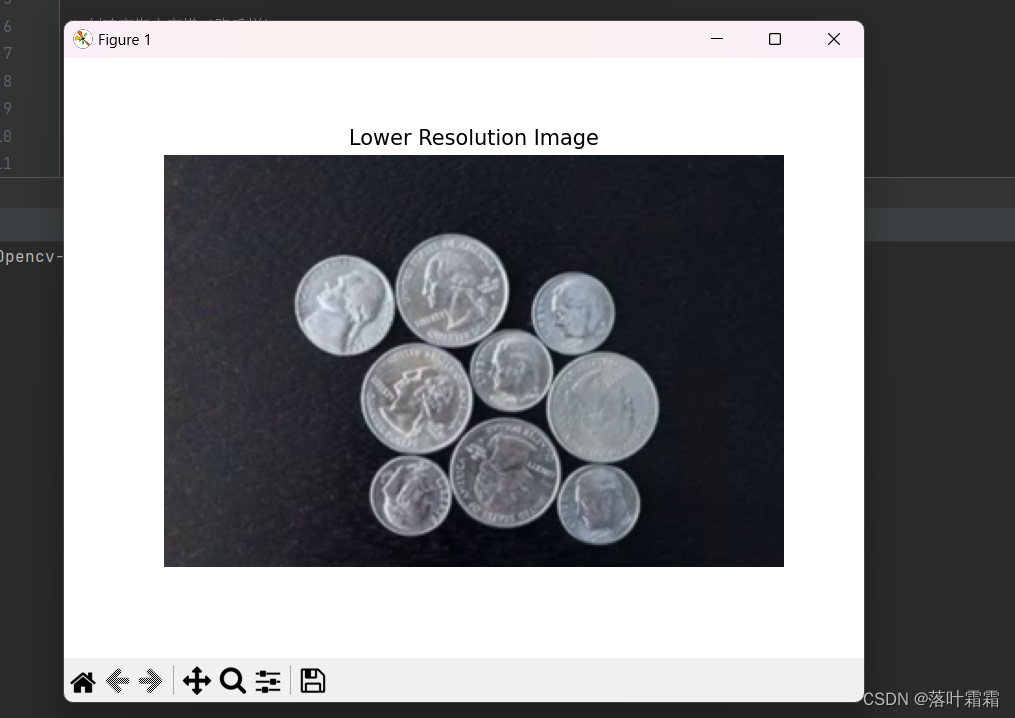
现在你可以使用函数 cv.pyrUp() 沿着图像金字塔向下移动。
higher_reso2 = cv.pyrUp(lower_reso)
需要记住的是,higher_reso2 不等于 higher_reso ,因为一旦减少了分辨率,你也丢失了信息。
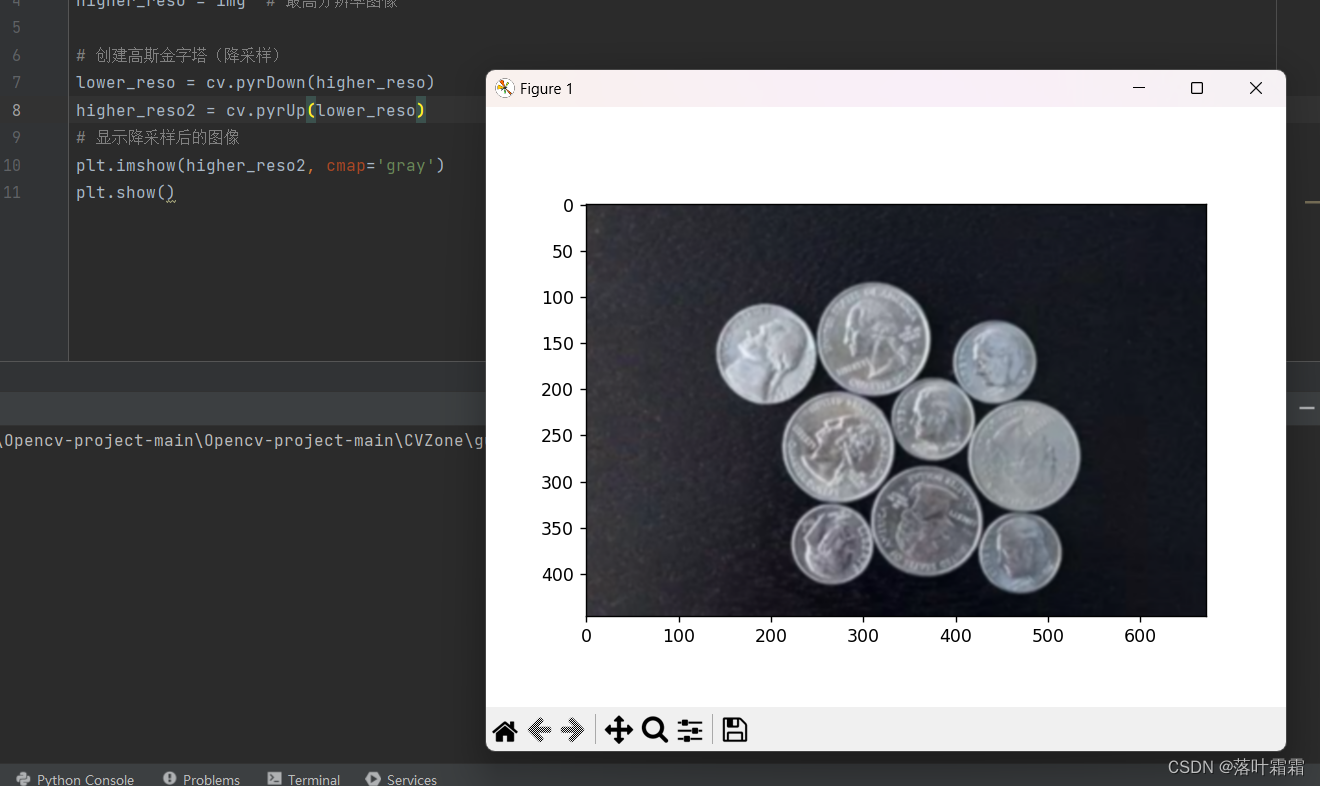
图像金字塔的其中一个应用是图像混合。举例来说,在图像拼接中,你需要将两个图像堆叠在一起,但是由于图像之间的不连续性,它的结果可能并太能令人满意。在这种情况下,使用金字塔进行图像合成可以实现无缝混合,而不会在图像中留下太多数据。这方面的一个经典例子是两种水果的混合,橙子和苹果。

加载图像: 从文件中加载橙子和苹果的图像。
生成高斯金字塔: 分别为橙子和苹果的图像生成高斯金字塔,包括6个层级。
生成拉普拉斯金字塔: 基于高斯金字塔,生成两幅图像的拉普拉斯金字塔。
合并图像的左右部分: 将苹果的左半部分和橙子的右半部分在每个金字塔级别连接起来,得到新的金字塔。
重新合成图像: 从合并后的金字塔开始,逐级向上构建图像,最终得到混合后的图像。
import cv2 as cv
import numpy as np
# 从文件加载橙子和苹果的图像
A = cv.imread('apple.jpg')
B = cv.imread('orange.jpg')
# 生成橙子的高斯金字塔
G = A.copy()
gpA = [G]
for i in range(6):
G = cv.pyrDown(G)
gpA.append(G)
# 生成苹果的高斯金字塔
G = B.copy()
gpB = [G]
for i in range(6):
G = cv.pyrDown(G)
gpB.append(G)
# 生成橙子的拉普拉斯金字塔
lpA = [gpA[5]]
for i in range(5, 0, -1):
GE = cv.pyrUp(gpA[i])
L = cv.subtract(gpA[i - 1], GE)
lpA.append(L)
# 生成苹果的拉普拉斯金字塔
lpB = [gpB[5]]
for i in range(5, 0, -1):
GE = cv.pyrUp(gpB[i])
L = cv.subtract(gpB[i - 1], GE)
lpB.append(L)
# 在每个级别上合并橙子和苹果的左右部分
LS = []
for la, lb in zip(lpA, lpB):
rows, cols, dpt = la.shape
ls = np.hstack((la[:, 0:cols // 2], lb[:, cols // 2:]))
LS.append(ls)
# 从拉普拉斯金字塔重建混合后的图像
ls_ = LS[0]
for i in range(1, 6):
ls_ = cv.pyrUp(ls_)
ls_ = cv.add(ls_, LS[i])
# 直接连接每一半的图像
real = np.hstack((A[:, :cols // 2], B[:, cols // 2:]))
# 保存混合图像和直接连接图像
cv.imwrite('Pyramid_blending.jpg', ls_)
cv.imwrite('Direct_blending.jpg', real)
轮廓:入门
当处理图像时,常常需要找到图像中的特定物体或形状。这时就用到了轮廓(Contours)的概念。轮廓是一种用于表示物体形状的曲线,这些曲线由连续的点组成。
在OpenCV中,可以使用cv.findContours()函数来寻找图像中的轮廓。这个函数需要一个二值图像作为输入,所以在使用之前通常会先进行阈值处理或者边缘检测。
一旦找到了轮廓,可以使用cv.drawContours()函数将轮廓画在图像上。这个函数的参数包括源图像、轮廓列表、轮廓的索引(如果想画特定的轮廓)、颜色和线条宽度等。
在寻找轮廓时,有一个需要注意的参数是轮廓逼近方法。这个方法决定了轮廓的存储方式。如果使用cv.CHAIN_APPROX_NONE,所有的边界点都会被存储。但是在大多数情况下,并不需要所有的点,只需要表示形状的关键点。这时就可以使用cv.CHAIN_APPROX_SIMPLE,它会删除冗余的点,用更少的点来表示同样的形状,从而节省内存。
通过使用cv.findContours()和cv.drawContours(),可以在图像中找到并标识出感兴趣的物体或形状。这是图像处理中非常常用的技术,尤其在物体检测和图像识别领域。
为了更好的准确性,使用二值图像。所以在寻找轮廓之前,应用阈值法或者Canny边缘检测。
•从OpenCV3.2开始,函数findContours() 不会再去修改源图像。
•在OpenCV中,寻找轮廓就像从黑色的背景中寻找白色的物体(前景)。所以需要记住的是,需要被找到的物体得是白色的,背景需要是黑色的。
import numpy as np
import cv2 as cv
im = cv.imread('img.png')
imgray = cv.cvtColor(im, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imgray, 127, 255, 0)
contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
想要绘制轮廓,使用函数 cv.drawContours 。只要有边界点,它也可用于绘制任何多边形。它的第一个参数是源图像,第二个参数是以 Python 列表传递的轮廓(译者注:上文得到的contours即可),第三个参数是轮廓索引(在绘制单个轮廓时很有用。要绘制所有轮廓,请传递 -1),其余参数是颜色、厚度等等。
•画出所有轮廓
cv.drawContours(img, contours, -1, (0, 255, 0), 3)
•只画出一个轮廓,比如第四个轮廓
cv.drawContours(img, contours, 3, (0, 255, 0), 3)
•但在大部分情况里面,下面这个写法会更好
cnt = contours[4]
cv.drawContours(img, [cnt], 0, (0, 255, 0), 3)
在图像处理中,轮廓是指相邻的具有相同颜色或者灰度强度的点所形成的边界。这些边界上的点的坐标通常以 (x, y) 形式存储。然而,在实际应用中,并不总是需要轮廓上的每一个点的信息。
举个例子,假设找到了一条直线的轮廓。在描述这条直线时,只需要知道它的两个端点的坐标,而不需要存储直线上的每一个点。这时,cv.CHAIN_APPROX_SIMPLE登场了。当传递cv.CHAIN_APPROX_SIMPLE给cv.findContours()函数时,它会智能地删除冗余的点,仅保留形状的关键点,比如端点,从而用更少的点来近似表示轮廓。这种处理方式不仅节省了内存空间,还使得后续的图像处理更加高效。