1.二分法手撕704（诀窍在于用合法区间判断）230810

• 左闭右闭:

while(left<=right)合法，middle=(left+right)/2,

if(nums[middle]>target)说明nums[middle]一定不是我们搜索的值，所以right=middle-1;

elseif(nums[middle]<target),同理left=middle+1.

else return middle;

return -1

• 左闭右开：同理。

记得left和right的初始赋值在左闭右开、左闭右闭也是不一样的。

class Solution {
public:
    int search(vector<int>& nums, int target) {
    // 左闭右闭写法
        int left = 0, right = nums.size() - 1;
        while(left <= right)
        {
            int middle = (left + right)/2;
            if(nums[middle] > target)
                right = middle - 1;
            else if(nums[middle] < target)
                left = middle + 1;
            else 
                return middle;
        }
        return -1;
    }
};
时间复杂度：O(logn)
空间复杂度：O(1)

并且，手写一遍流程就会发现对于middle=int(12.5)这种对于left+right为奇数的判断是多余的，没有必要考虑。

2.原地移除元素手撕27（面试官会让用双指针法，降低时间复杂度）230811

诀窍在于记住两个指针代表什么。

快指针需要找到下一个要填进新数组的元素；慢指针需要获取新数组中需要更新的位置。

时间复杂度：O(n) 空间复杂度：O(1)

3.有序数组的平方977（双指针法 但非快慢指针，而是左右指针，从最后开始插入）230811

半年前美滋滋sort暴力，时间复杂度是 O(n + nlogn)， 可以说是O(nlogn)的时间复杂度

现在使用双指针

4.长度最小的子数组209(是双指针，但是取中间集合，也即滑动窗口)

for循环的索引，一定是表示滑动窗口的终止位置。

for里面嵌套一个while，while里面的顺序要搞清楚，不能i++之后再减去sum[i]。

另外，vector的sum只能由accumulate带三个参数进行运算求得。

5.螺旋矩阵59

模拟题，不涉及算法，关键点在于边界的处理。

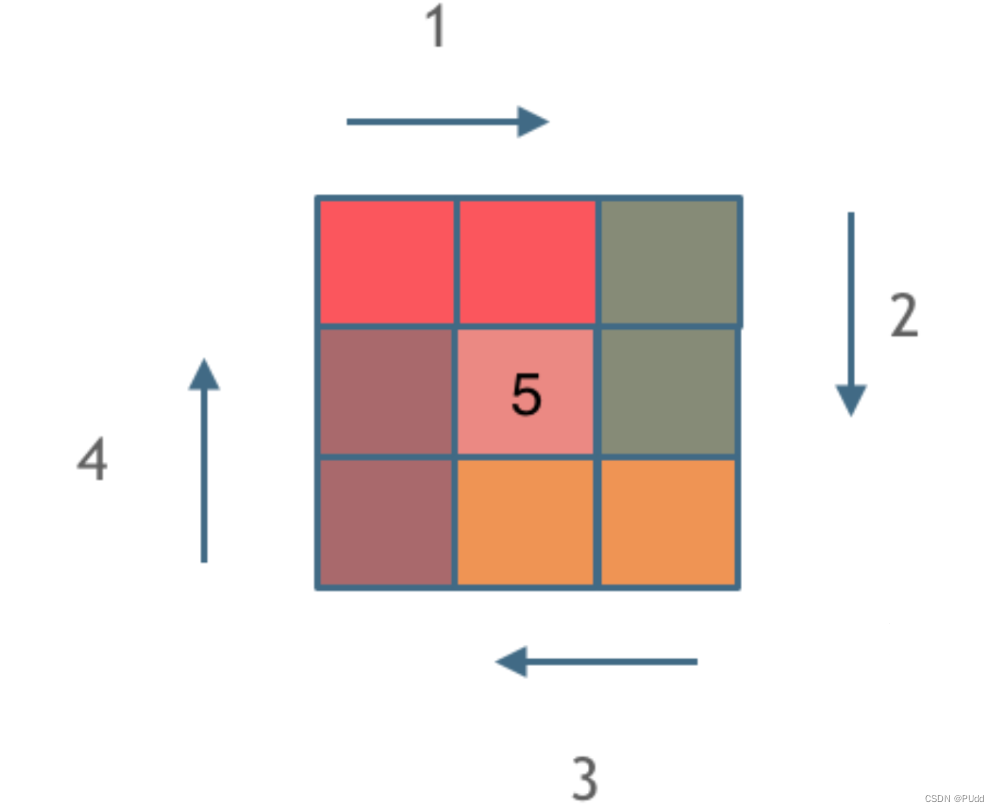
①转几圈？左栏为n²，右栏为圈数

1->0圈+1个, 4->1圈

9->1圈+1个, 16->2圈

25->2圈+1个

……

也即，n/2圈。奇数最后+1.

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int startx = 0;
        vector<vector<int>>matrix(n,vector<int>(n));
        int record = n/2;
        int val = 1;
        while(record--)
        {
            for(int i = startx, j = startx; j < n - startx - 1; j++){
                matrix[i][j]= val++;
            }
            for(int i = startx, j = n - startx - 1; i < n - startx - 1 ; i++){
                matrix[i][j]= val++;
            }
            for(int i = n - startx - 1, j = n - startx - 1; j > startx; j--){
                matrix[i][j]= val++;
            }
            for(int i = n - startx - 1, j = startx; i > startx; i--){
                matrix[i][j]= val++;
            }
            startx++;
        }
        if (n%2 == 1)
            matrix[n/2][n/2] = val; 
        return matrix;
    }
};

注意，      vector<vector<int>>matrix(m,vector<int>(n)); 里面，是m行n列。