9、电路综合-基于简化实频的任意幅频响应的微带电路设计
网络综合和简化实频理论学习概述中的1-8介绍了SRFT的一些基本概念和实验方法,终于走到了SRFT的究极用途,给定任意响应直接综合出微带电路。
1、任意幅频响应的微带电路设计用途
我们演示了采用相应传输线的经典微波滤波器的设计过程。设计方法的第一步是选择合适的传递函数。显然,传递函数的形式必须反映设计要求。对于许多实际情况,使用通过巴特沃斯或切比雪夫多项式构造的现成低通类型原型函数可能就足够了。
然而,对于某些应用,换能器功率增益(TPG)的期望形状可以由所考虑的问题以任意方式决定。例如,可以利用补偿信道失真的无损滤波器来均衡通信信道的增益失真。
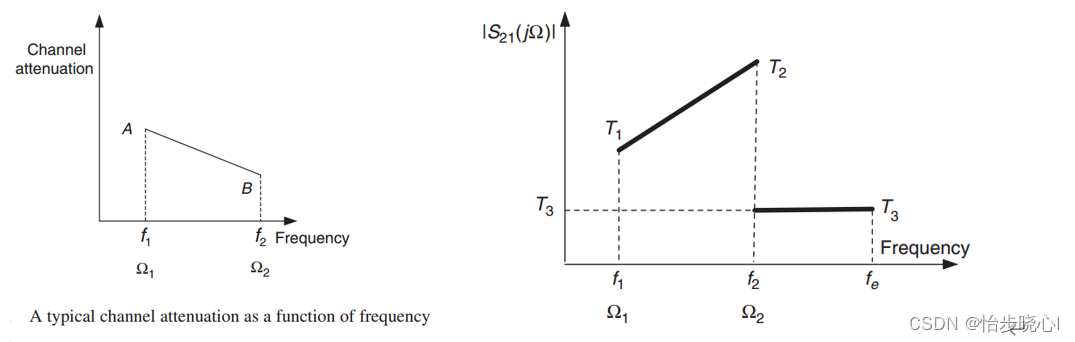
当然,这种设计方法也可以用于匹配电路的设计分析(根据匹配目标之间生成对应的微带线电路)。
2、之前的一些回顾与总结
之前也给出了一些电路综合的案例,但是这些案例必须基于解析函数形式的S参数,在更为一般的情况下我们难以基于此去完成设计,我们往往需要基于要设计电路的幅频响应和相频响应去设计实际的电路:
5、电路综合-超酷-基于S11参数直接综合出微带线电路图
基于给定的S11参数的表达式综合出其对应的微带电路图,注意此处的S11参数表达式需要是解析形式(即要是函数表达式的形式)
6、电路综合-基于简化实频的SRFT微带线切比雪夫低通滤波器设计
基于切比雪夫函数进行电路综合,基于目标参数直接进行电路综合得到其对应的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
7、电路综合-基于简化实频的SRFT微带线巴特沃兹低通滤波器设计
基于巴特沃斯函数进行电路综合,基于目标参数直接进行电路综合得到其对应的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
8、电路综合-基于简化实频的SRFT微带线的带通滤波器设计
基于巴特沃斯与切比雪夫函数进行电路综合,基于目标参数直接进行电路综合得到其对应的带通的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
3、任意幅频响应的微带电路设计步骤
假设我需要设计一个具备如下幅频特性的微带线电路,频率f1为0GHz,在此频率的S21的模值为1;频率f2为1GHz,在此频率的S21的模值为0,并在1-3GHz内都要求S21的模值为0(此特性用于确定微带线的电长度)。
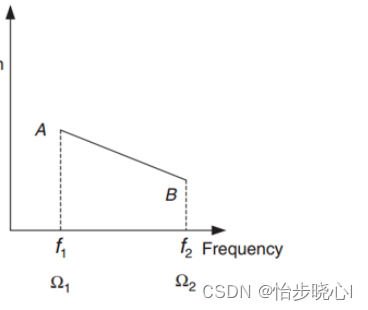
STEP1:设计目标具体现化,将要设计的目标转化为数组的形式,数组覆盖的频率范围为0-3GHz,此处使用长度为58的数组对此目标进行存储,值得注意的是,此数组越大优化的速度也会越慢:

STEP2:确定实现此结构所需的电路结构,其主要需要确定的是实现此幅频响应的阶数n,通过前面几个教程的学习,我们知道基于电路的结构可以直接确定F(lamda),只需要确定H(lamda)的系数就可以进行电路综合了。
意思就是,我们需要得到符合如上幅频响应的H(lamda)的系数,就可以使用SRFT进行电路综合了,这一步需要使用最优化算法来进行系数的求解。定义的误差函数如下(简单来说就是实际值减去目标值,最优化的目标是使最终误差极小为0):
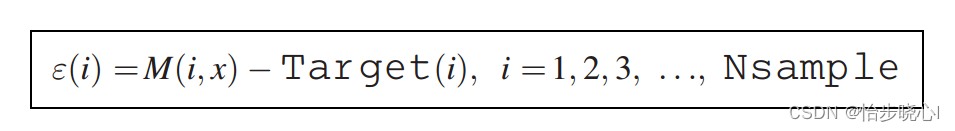
在MATLAB中,可以使用lsqnonlin完成此优化过程,其使用教程如非线性最小二乘求解器
STEP3:在一定次数的迭代求解后,可以得到其对应的一组解,此解就是h的系数,由此进行电路综合。具体综合过程可以参考之前的教程。
4、Matlab编程实现
clear
clc
% 使用1GHZ的微带线,最高控制到3GHz
f=1;
fe=3;
we=2*pi*fe;
tau=pi/2/we;
ele_l=360*tau*f;
%使用6个级联微带线进行设计
k=6;
%在DC处无零点
q=0;
%初始化H的系数
h=[1 1 1 1 1 1 1];
disp(['此处使用在',num2str(f/1e9),'GHz下电长度为',num2str(ele_l),'°的微带线进行实现']);
%0-3GHz的点数
Nopt=57;
fr_opt=linspace(0,3,Nopt+1);
% 定义S21参数的模值
mag=[1,0.952631578947368,0.905263157894737,0.857894736842105,0.810526315789474,0.763157894736842,0.715789473684211...
,0.668421052631579,0.621052631578947,0.573684210526316,0.526315789473684,0.478947368421053,0.431578947368421...
,0.384210526315789,0.336842105263158,0.289473684210526,0.242105263157895,0.194736842105263,0.147368421052631...
,0.100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000...
,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000...
,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000...
,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000...
,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000...
,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000,0.0100000000000000...
,0.0100000000000000,0.0100000000000000,0.0100000000000000];
% 定义相位,此处只设计幅值,相位随意了
phase=linspace(0,0,Nopt+1);
% 画出目标电路的幅度
figure (1)
plot(fr_opt,mag)
xlabel('Frequency')
ylabel('MAG-S21')
title('要设计的微带线的目标S21参数')
% 运行优化算法
n1=length(h);
n=n1-1;
h(n+1)=0;
for i=1:n
x0(i)=h(i);
end
% Call optimization with no transformer
OPTIONS=optimset('MaxFunEvals',20000,'MaxIter',50000);
x=lsqnonlin('objective',x0,[],[],OPTIONS,fe,q,k,fr_opt,mag, phase);
h(n+1)=0;
for i=1:n
h(i)=x(i);
end
% 基于优化得到的h计算其他参数
[G,H,F,g]=SRFT_htoG(h,q,k);
tau=1/4/fe;
N=length(mag);
j=sqrt(-1);
% 将得到的解析形式画图
for i=1:N
teta=2*pi*tau*fr_opt(i);
omega=tan(teta);
lmbda=j*tan(teta);
fval=(-1)^q*(lmbda)^q*(1-lmbda^2)^(k/2);
freal=real(fval);
fimag=imag(fval);
gval=polyval(g,lmbda);
greal=real(gval);
gimag=imag(gval);
S21=fval/gval;
MS21(i)=abs(S21);
phase_f=atan(fimag/freal);
phase_g=atan(gimag/greal);
phase_S21(i)=phase_f-phase_g;
ph(i)=teta;
fr(i)=fr_opt(i);
end
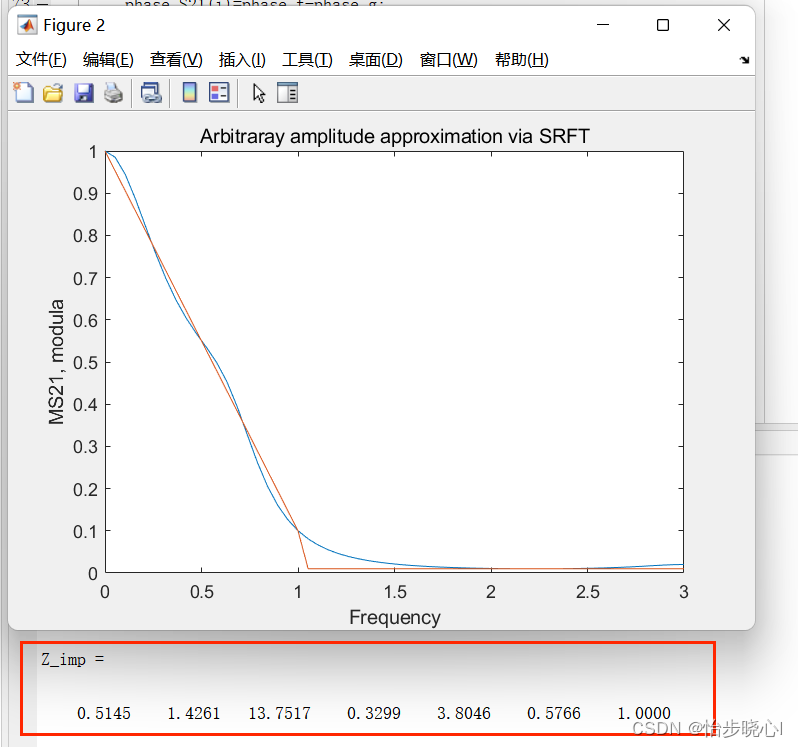
figure(2)
plot(fr,MS21, fr_opt,mag)
xlabel('Frequency')
ylabel('MS21, modula')
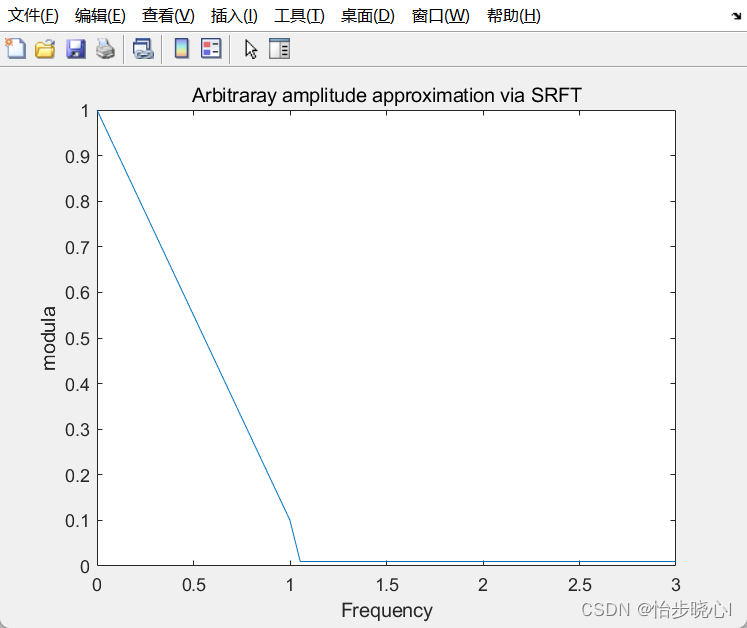
title('Arbitraray amplitude approximation via SRFT')
%------------------------------------
% 综合得到所需的微带电路
[Z_imp]=UE_sentez(h,g)
运行结果,图中是理想与实际的对比:
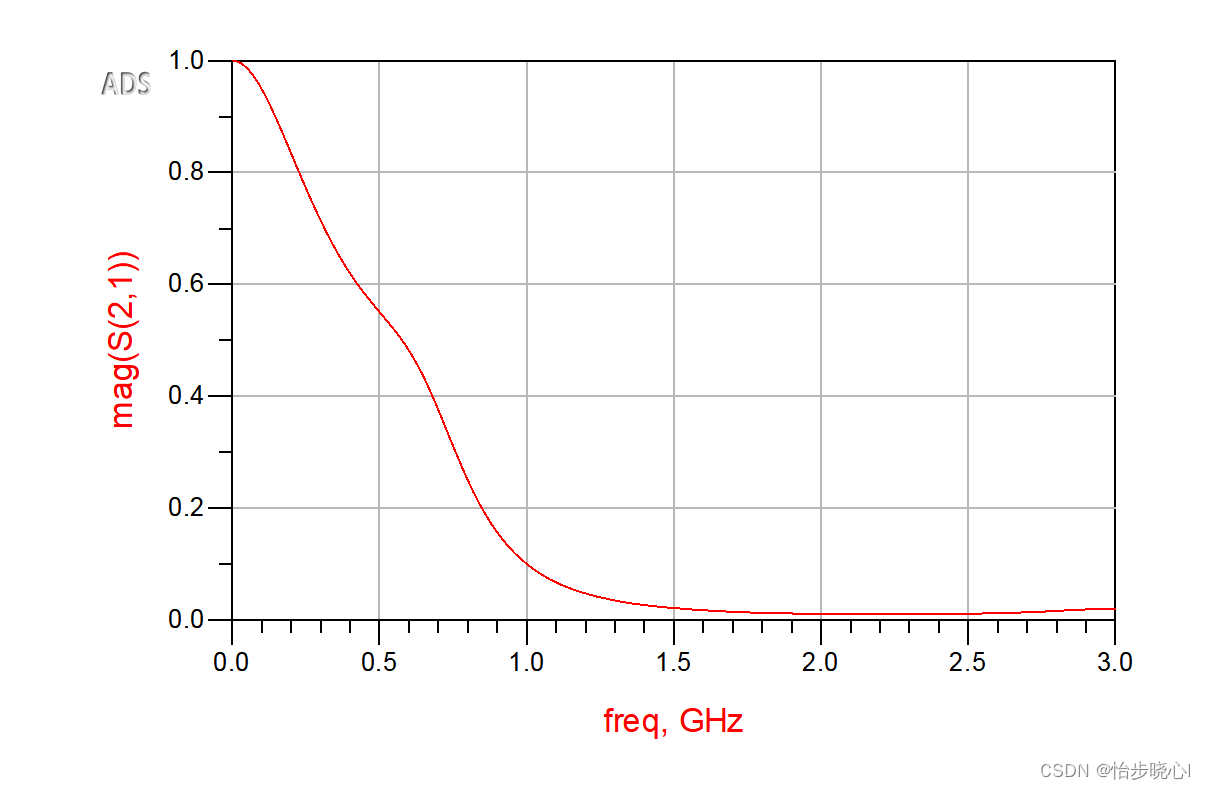
5、ADS验证
电路图构建:
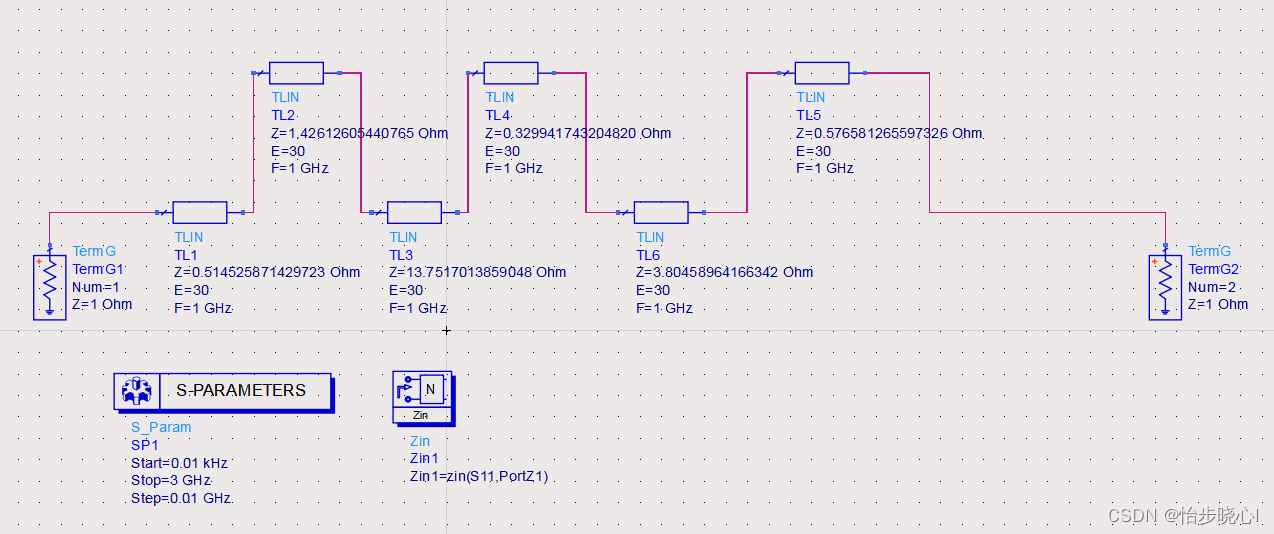
仿真结果如下,可见和设计目标基本一致: