C++进阶篇3---二叉搜索树(Binary Search Tree)

news2024/11/24 4:01:35

一、二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树

根据二叉搜索树的性质，我们很容易看出它的中序遍历是升序，下面画一个二叉搜索树，可以试着用中序遍历遍历一遍，对二叉树有所遗忘的可以去看看二叉树详解

 

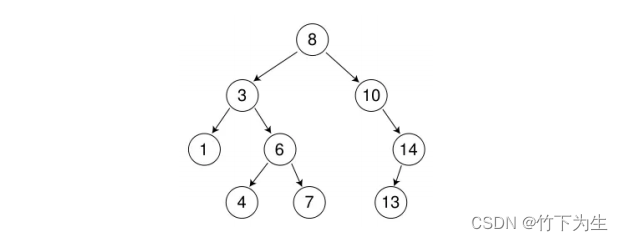
二、二叉搜索树的实现

//定义结点
template<class T>
struct BSTreeNode {
	T val;
	BSTreeNode* left;
	BSTreeNode* right;

	BSTreeNode(const T& x)
		:val(x)
		,left(nullptr)
		,right(nullptr)
	{}
};

template<class T>
class BSTree {
	typedef BSTreeNode<T> Node;
public:
    void InOrder();//中序遍历
    Node* Find(const T& x);//查找
	bool Insert(const T& x);//插入
	bool Erase(const T& x);//删除
private:
    Node*_root;
};

注意：下面代码涉及的递归函数都是写了两层，一层供对象调用，一层实现底层逻辑，因为_root被设置为了私有成员，而树的操作基本都需要遍历，所以通过成员函数实现对_root的使用

1.中序遍历

//这里二叉树的递归函数建议写两层，因为_root是私有成员只能在类内访问
void _InOrdered(Node* root) //该函数可以设为私有/保护，仅供类内使用，具体在场景
{
	if (root == __nullptr)
		return;
	_InOrdered(root->left);
	cout << root->val << " ";
	_InOrdered(root->right);
}

void InOrdered()
{
	_InOrdered(_root);
	cout << endl;
}

2.查找

2.1迭代

Node* Find(const T& x) {
	Node* cur = _root;
	while (cur) {
		if (cur->val == x)
			return cur;
		else if (cur->val > x)
			cur = cur->left;
		else
			cur = cur->right;
	}
	return nullptr;
}

2.2递归

	
Node* _FindR(Node* root, const T& x) 
{
	if (root->val > x)
		return _FindR(root->left, x);
	else if (root->val < x)
		return _FindR(root->right, x);
	else
		return root;
	return nullptr;
}

Node* FindR(const T& x) 
{
	return _FindR(_root, x);
}

3.插入

  • 二叉搜索树中没有重复元素

3.1迭代

bool Insert(const T& x) 
{
	if (_root == nullptr) //为空树，直接插入
    {
		_root = new Node(x);
		return true;
	}
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur) 
    {
		parent = cur;
		if (cur->val < x)
			cur = cur->right;
		else if (cur->val > x)
			cur = cur->left;
		else//出现该值出现过
			return false;
    }
	Node* newnode = new Node(x);
	if (parent->val > x) parent->left = newnode;
	else parent->right = newnode;
	return true;
}

3.2递归

bool _InsertR(Node*& root,const T& x) //注意这里的引用
{
	if (root == nullptr) 
    {
		root = new Node(x);//这是引用，不是变量，不用担心连接问题，本质和用二级指针一样
		return true;
	}
	if (root->val > x)
		return _InsertR(root->left, x);
	else if (root->val < x)
		return _InsertR(root->right, x);
	else
		return false;
}

bool InsertR(const T& x) {
	return _InsertR(_root, x);
}

4.删除（重点）

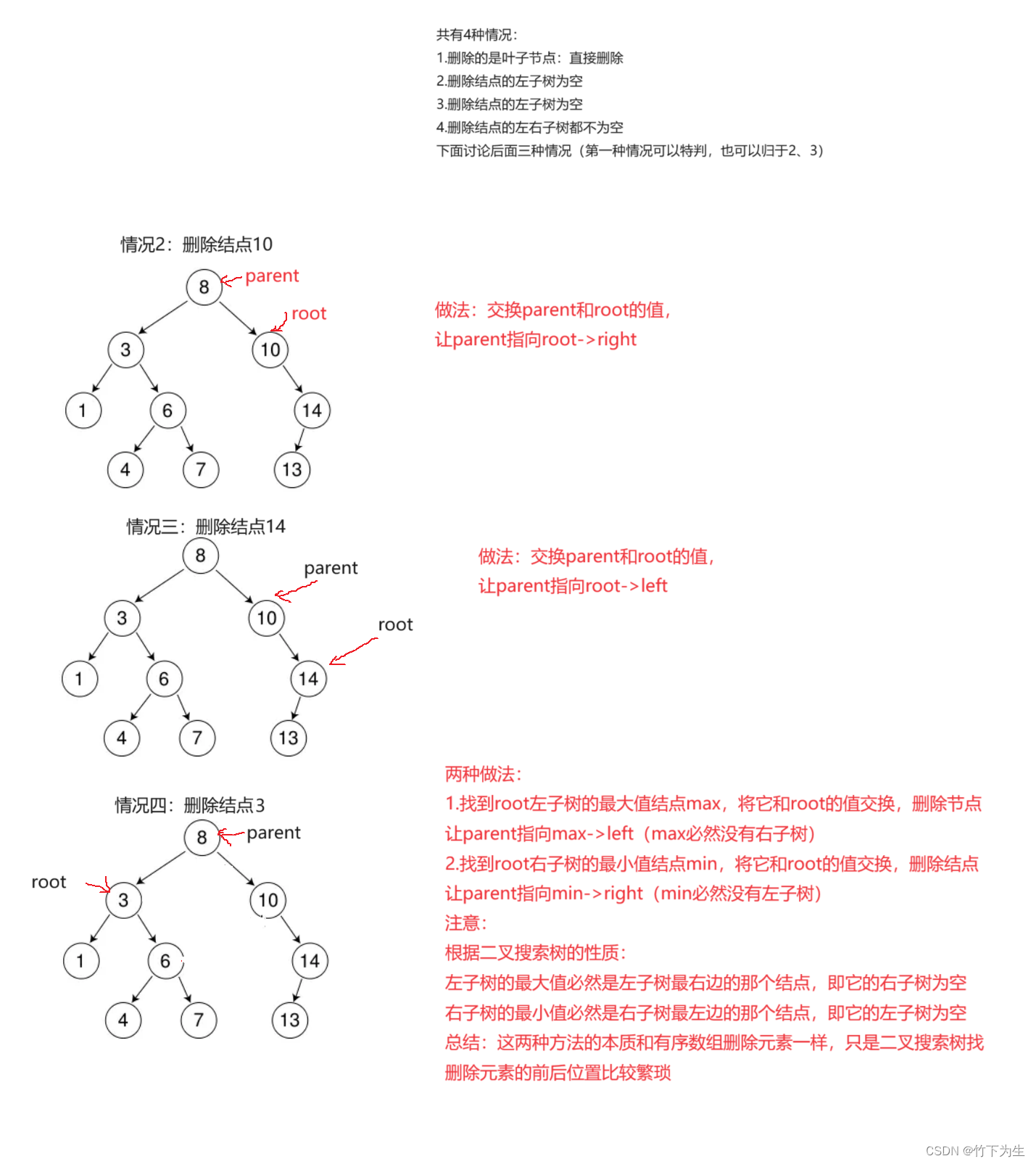
 4.1迭代

bool Erase(const T& x) 
{
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur) 
    {
		int val = cur->val;
		if (x < val) 
		{
			parent = cur;
			cur = cur->left;
		}
		else if (x > val) 
		{
			parent = cur;
			cur = cur->right;
		}
		else 
		{
			if (cur->left == nullptr) //左为空
			{
				if (parent->val > x)
					parent->left = cur->right;
				else
					parent->right = cur->right;
			}
			else if (cur->right == nullptr)//右为空
			{
				if (parent->val > x)
					parent->left = cur->left;
				else
					parent->right = cur->left;
			}
			else//左右都不为空
			{//这里采取在右子树种找最小结点
				Node* L = cur->right;
				Node* fa = cur;
				while (L->left) 
                {
					fa = L;
					L = L->left;
				}
				swap(L->val, cur->val);
                
				if (fa != cur)
					fa->left = nullptr;
				else//这里需要注意如果最小结点就是右子树的根结点的情况
					fa->right = L->right;
				cur = L;
			}
			delete cur;
			return true;
		}
	}
	return false;
}

4.2递归

bool _EraseR(Node*& root, const T& x) //注意这里的引用
{
	if (root == nullptr)
		return false;
	if (root->val > x)
		return _EraseR(root->left, x);
	else if (root->val < x)
		return _EraseR(root->right, x);
	else 
	{
		if (root->left == nullptr) 
		{
			Node* del = root;
			root = root->right;
			delete del;
			return true;
		}
		else if (root->right == nullptr) 
		{
			Node* del = root;
			root = root->left;
			delete del;
			return true;
		}
		else
		{
			Node* subleft = root->right;//找比它大的第一个数字
			while (subleft->left)
				subleft = subleft->left;
	
			swap(subleft->val, root->val);
			return _EraseR(root->right, x);//将问题转化为更小的子问题
		}
	}
}

bool EraseR(const T& x) 
{
	return _EraseR(_root, x);
}

三、完整版

template<class T>
struct BSTreeNode {
	T val;
	BSTreeNode* left;
	BSTreeNode* right;

	BSTreeNode(const T& x)
		:val(x)
		,left(nullptr)
		,right(nullptr)
	{}
};

template<class T>
class BSTree {
	typedef BSTreeNode<T> Node;
public:
	bool Insert(const T& x) {
		if (_root == nullptr) {
			_root = new Node(x);
			return true;
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur) {
			parent = cur;
			if (cur->val < x) {
				cur = cur->right;
			}else if (cur->val > x) {
				cur = cur->left;
			}else{
				return false;
			}
		}
		Node* newnode = new Node(x);
		if (parent->val > x) parent->left = newnode;
		else parent->right = newnode;
		return true;
	}

	Node* find(const T& x) {
		Node* cur = _root;
		while (cur) {
			if (cur->val == x)
				return cur;
			else if (cur->val > x)
				cur = cur->left;
			else
				cur = cur->right;
		}
		return nullptr;
	}

	bool erase(const T& x) {
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur) {
			int val = cur->val;
			
			if (x < val) 
			{
				parent = cur;
				cur = cur->left;
			}
			else if (x > val) 
			{
				parent = cur;
				cur = cur->right;
			}
			else 
			{
				if (cur->left == nullptr) //左为空
				{
					if (parent->val > x)
						parent->left = cur->right;
					else
						parent->right = cur->right;
				}
				else if (cur->right == nullptr)//右为空
				{
					if (parent->val > x)
						parent->left = cur->left;
					else
						parent->right = cur->left;
				}
				else//左右都不为空
				{
					Node* L = cur->right;
					Node* fa = cur;
					while (L->left) {
						fa = L;
						L = L->left;
					}
					swap(L->val, cur->val);
					if (fa != cur)
						fa->left = nullptr;
					else
						fa->right = L->right;
					cur = L;
				}
				delete cur;
				return true;
			}
		}
		return false;
	}


	void _InOrdered(Node* root) {
		if (root == __nullptr)
			return;
		_InOrdered(root->left);
		cout << root->val << " ";
		_InOrdered(root->right);
	}

	void InOrdered() {
		_InOrdered(_root);
		cout << endl;
	}


	Node* FindR(const T& x) {
		return _FindR(_root, x);
	}

	bool InsertR(const T& x) {
		return _InsertR(_root, x);
	}

	bool EraseR(const T& x) {
		return _EraseR(_root, x);
	}

	//BSTree() {}
	
	BSTree() = default;//强制生成默认构造
	~BSTree()
	{
		Destroy(_root);
	}

	BSTree(const BSTree& t) 
	{
		_root = Copy(t._root);
	}

	BSTree& operator=(const BSTree t)
	{
		swap(t._root);
		return *this;
	}
private:
	Node* Copy(Node* root) {
		if (root == nullptr)
			return nullptr;
		Node* newnode = new Node(root->val);
		newnode->left = Copy(root->left);
		newnode->right = Copy(root->right);
		return newnode;
	}

	void Destroy(Node*& root) {
		if (root == nullptr)
			return;
		Destroy(root->left);
		Destroy(root->right);
		delete root;
		root = nullptr;
	}

	bool _EraseR(Node*& root, const T& x) {
		if (root == nullptr)
			return false;
		if (root->val > x)
			return _EraseR(root->left, x);
		else if (root->val < x)
			return _EraseR(root->right, x);
		else 
		{
			if (root->left == nullptr) 
			{
				Node* del = root;
				root = root->right;
				delete del;
				return true;
			}
			else if (root->right == nullptr) 
			{
				Node* del = root;
				root = root->left;
				delete del;
				return true;
			}
			else
			{
				Node* subleft = root->right;//找比它大的第一个数字
				while (subleft->left) {
					subleft = subleft->left;
				}
				swap(subleft->val, root->val);
				return _EraseR(root->right, x);
			}
		}
	}

	bool _InsertR(Node*& root,const T& x) {
		if (root == nullptr) {
			root = new Node(x);
			return true;
		}
		if (root->val > x)
			return _InsertR(root->left, x);
		else if (root->val < x)
			return _InsertR(root->right, x);
		else
			return false;
	}


	Node* _FindR(Node* root, const T& x) {
		if (root->val > x)
			return _FindR(root->left, x);
		else if (root->val < x)
			return _FindR(root->right, x);
		else
			return root;
		return nullptr;
	}
private:
	Node* _root = nullptr;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1147693.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

java之输入与输出的详细介绍

java之输入与输出的详细介绍

文章目录 输出的相关格式使用 Scanner 类进行控制台输入步骤&#xff1a;示例&#xff1a; 如何格式化输出&#xff1f;1. 使用 System.out.printf2. 使用 String.format printf与println 的区别printfprintln主要区别&#xff1a; 输出的相关格式 控制台输入是指通过命令行或…
阅读更多...
JAVA中的垃圾回收器(2)------G1

JAVA中的垃圾回收器(2)------G1

一)G1垃圾回收器:-XX:UseG1GC:使用G1收集器 1)垃圾收集器迭代停顿时间越少越好&#xff0c;但是垃圾回收的总时间会增多&#xff0c;默认暂停时间默认是200ms&#xff0c;G1的内部底层算法非常复杂比CMS复杂&#xff0c;如果大内存&#xff0c;G1还比较有效果&#xff0c;但是如…
阅读更多...
leetcode-数组

leetcode-数组

1.二分法手撕704&#xff08;诀窍在于用合法区间判断&#xff09;230810 左闭右闭: while(left<right)合法&#xff0c;middle(leftright)/2, if(nums[middle]>target)说明nums[middle]一定不是我们搜索的值&#xff0c;所以rightmiddle-1; elseif(nums[middle]<targe…
阅读更多...
基于单片机的太阳跟踪系统的设计

基于单片机的太阳跟踪系统的设计

欢迎大家点赞、收藏、关注、评论啦 &#xff0c;由于篇幅有限&#xff0c;只展示了部分核心代码。 技术交流认准下方 CSDN 官方提供的联系方式 文章目录 概要 一、设计的主要内容二、硬件电路设计2.1跟踪控制方案的选择2.1.1跟踪系统坐标系的选择2.2系统总体设计及相关硬件介绍…
阅读更多...
9、电路综合-基于简化实频的任意幅频响应的微带电路设计

9、电路综合-基于简化实频的任意幅频响应的微带电路设计

9、电路综合-基于简化实频的任意幅频响应的微带电路设计 网络综合和简化实频理论学习概述中的1-8介绍了SRFT的一些基本概念和实验方法&#xff0c;终于走到了SRFT的究极用途&#xff0c;给定任意响应直接综合出微带电路。 1、任意幅频响应的微带电路设计用途 我们演示了采用…
阅读更多...
Flask基本教程以及Jinjia2模板引擎简介

Flask基本教程以及Jinjia2模板引擎简介

flask基本使用 直接看代码吧&#xff0c;非常容易上手&#xff1a; # 创建flask应用 app Flask(__name__)# 路由 app.route("/index", methods[GET]) def index():return "FLASK&#xff1a;欢迎访问主页&#xff01;"if __name__ "__main__"…
阅读更多...
【多线程面试题九】、说一说sleep()和wait()的区别

【多线程面试题九】、说一说sleep()和wait()的区别

文章底部有个人公众号&#xff1a;热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享&#xff1f; 踩过的坑没必要让别人在再踩&#xff0c;自己复盘也能加深记忆。利己利人、所谓双赢。 面试官&#xff1a;说一说sleep()和wait()的…
阅读更多...
如何使用 Docker 搭建 Jenkins 环境？从安装到精通

如何使用 Docker 搭建 Jenkins 环境？从安装到精通

不少兄弟搭 jenkins 环境有问题&#xff0c;有的同学用 window, 有的同学用 mac&#xff0c; 有的同学用 linux。 还有的同学公司用 window, 家里用 mac&#xff0c;搭个环境头发掉了一地。。。 这回我们用 docker 去搭建 jenkins 环境&#xff0c;不管你是用的是什么系统&…
阅读更多...
方太描画未来厨房的模样

方太描画未来厨房的模样

作者 | 辰纹 来源 | 洞见新研社 不知不觉中&#xff0c;iPhone已经更新到15代了&#xff0c;家里的电视变成了越来越轻薄的液晶屏&#xff0c;过去被称为“老三样”的富康&#xff0c;捷达、桑塔纳&#xff0c;如今也被以特斯拉为代表的新能源智能汽车们所取代…… 类似以上的…
阅读更多...
第五章 I/O管理 一、I/O设备的基本概念和分类

第五章 I/O管理 一、I/O设备的基本概念和分类

目录 一、什么是I/O设备 1、定义&#xff1a; 2、按特性分类&#xff1a; 3、按传输速率分类&#xff1a; 4、按信息交换的方式分类&#xff1a; 二、总结 一、什么是I/O设备 1、定义&#xff1a; I/O设备就是可以将数据输入到计算机&#xff0c;或者可以接收计算机输出…
阅读更多...
＜C++＞ vector模拟实现

＜C++＞ vector模拟实现

目录 前言 一、定义命名空间 二、构造函数 三、拷贝构造 四、赋值运算符重载 五、push_back && reserve 六、深拷贝问题 七、iterator 迭代器 1. 可读可写 2. 只读 八、operator[ ] 1. 可读可写 2. 只读 九、insert 问题&#xff1a;内部迭代器失效 十、erase 十一、re…
阅读更多...
【网络安全】Seeker内网穿透追踪定位

【网络安全】Seeker内网穿透追踪定位

Seeker追踪定位对方精确位置 前言一、kali安装二、seeker定位1、ngrok平台注册2、获取一次性邮箱地址3、ngrok平台登录4、ngrok下载5、ngrok令牌授权6、seeker下载7、运行seeker定位8、运行隧道开启监听9、伪装链接10、用户点击&#xff08;获取定位成功&#xff09;11、利用经…
阅读更多...
（速进）完美解决“用户在命令行上发出了 EULAS_AGREED=1，表示不接受许可协议。”以及“此产品安装程序不支持降级”

（速进）完美解决“用户在命令行上发出了 EULAS_AGREED=1，表示不接受许可协议。”以及“此产品安装程序不支持降级”

安装VMware时候&#xff0c;出现以下两种情况的原因是&#xff1a;未彻底卸载&#xff08;之前安装过VMware&#xff09;&#xff0c;例如&#xff1a;还有相关配置信息、注册表信息等。只要彻底清理就可以解决此问题。 网上很多帖子使用了powershell里的命令 例如&#xff1…
阅读更多...
Linux病毒疯狂增长，我们该如何…

Linux病毒疯狂增长，我们该如何…

导读国家信息中心日前与瑞星联合发布的《2017年上半年中国网络安全报告》&#xff08;以下简称《报告》&#xff09;指出&#xff0c;目前Linux系统病毒已快速增长。《报告》对2017年1至6月的网络安全现状与趋势进行统计、研究和分析后指出&#xff0c;Linux系统的勒索软件数量…
阅读更多...
帆软finereport10.0 多个筛选框根据不同条件必须选一个才能查询

帆软finereport10.0 多个筛选框根据不同条件必须选一个才能查询

效果&#xff1a; 方法一&#xff1a; 方法二&#xff1a; 方法一&#xff1a;在查询里写上一段js&#xff0c;此方法会把端口和IP暴露出来&#xff0c;方法二比较完美。 var diff this.options.form.getWidgetByName("diff").getValue();//正反向 var fllh …
阅读更多...
【多线程面试题 八】、说一说Java同步机制中的wait和notify

【多线程面试题 八】、说一说Java同步机制中的wait和notify

文章底部有个人公众号&#xff1a;热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享&#xff1f; 踩过的坑没必要让别人在再踩&#xff0c;自己复盘也能加深记忆。利己利人、所谓双赢。 面试官&#xff1a;说一说Java同步机制中的…
阅读更多...
Day 12 python学习笔记

Day 12 python学习笔记

模块 内置模块 sys模块 概述&#xff1a;Python 的 sys 模块提供访问解释器使用或维护的变量&#xff0c;和与解释器进行交互的函数。通俗来讲&#xff0c;sys 模块为程序与 Python 解释器的交互&#xff0c;提供了一系列的函数和变量&#xff0c;用于操控 Python 运行时的环境…
阅读更多...
多输入多输出 | Matlab实现k-means-ELM（k均值聚类结合极限学习机）多输入多输出组合预测

多输入多输出 | Matlab实现k-means-ELM（k均值聚类结合极限学习机）多输入多输出组合预测

多输入多输出 | Matlab实现k-means-ELM&#xff08;k均值聚类结合极限学习机&#xff09;多输入多输出组合预测 目录 多输入多输出 | Matlab实现k-means-ELM&#xff08;k均值聚类结合极限学习机&#xff09;多输入多输出组合预测预测效果基本描述程序设计参考资料 预测效果 基…
阅读更多...
lazarus开发：提升sqlite数据插入速度

lazarus开发：提升sqlite数据插入速度

目录 1 前言 2 优化数据容器 3 开启事务插入数据 4 其他方面优化 1 前言 近期有一个需求是向数据库中插入excel文件中的10万多条数据&#xff0c;接近70个字段。最初整个插入数据时间是大约40分钟&#xff0c;经过优化调整后&#xff0c;大幅优化为大约5分钟。这里简单介绍…
阅读更多...
CV计算机视觉每日开源代码Paper with code速览-2023.10.27

CV计算机视觉每日开源代码Paper with code速览-2023.10.27

精华置顶 墙裂推荐&#xff01;小白如何1个月系统学习CV核心知识&#xff1a;链接 点击CV计算机视觉&#xff0c;关注更多CV干货 论文已打包&#xff0c;点击进入—>下载界面 点击加入—>CV计算机视觉交流群 1.【基础网络架构&#xff1a;Transformer】&#xff08;Ne…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023