-
实验内容
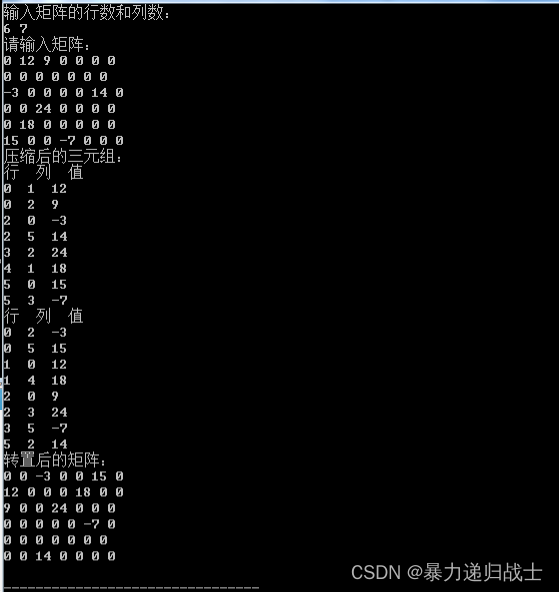
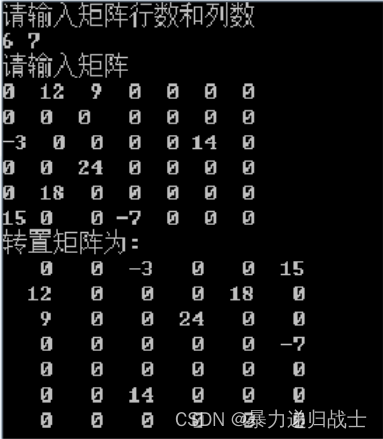
1、(1)题目要求:如图所示,任意输入一个稀疏矩阵M,用三元组顺序表压缩存储该稀疏矩阵M,然后求其转置矩阵T,并输出转置矩阵T。
三元组的表示和初始化,用线性表
typedef struct{
int i,j;
int val;
}Triplet;
typedef struct{
Triplet *elem;
int tu,mu,nu;//个数,行数,列数
}SqTriplet;
bool InitTriplet(SqTriplet &T,int rowSize,int colSize)
{
T.elem=new Triplet[rowSize*colSize/5];
if(!T.elem) return false;
T.tu=0;
T.mu=rowSize;
T.nu=colSize;
return true;
}矩阵压缩函数
void compress(int M[][10],SqTriplet &T,int rowSize,int colSize)
{//压缩函数
for(int row=0;row<rowSize;row++)
{
for(int col=0;col<colSize;col++)
{
if(M[row][col]!=0)
{//非零项赋值,个数加一
// T.(elem+T.length)->row=i;
T.elem[T.tu].i=row;
T.elem[T.tu].j=col;
T.elem[T.tu].val=M[row][col];
T.tu++;
}
}
}
}转置函数(快速转置)
用一个nums数组记录某一列前前面的所有列一共有多少个数,随后再转置,只需对三元组扫描三次。
void reserve(SqTriplet T,SqTriplet &T1)
{//T转置==>T1
//记录每一列元素的个数
int nums[T.nu]={0};
for(int k=0;k<T.tu;k++)
{
nums[T.elem[k].j]++;
}
//记录每一列之前的列一共有多少个数据[1,3,5,2,3,4,5]
// nums[i] =[0,i-1]列元素个数 [0,1,4,9,11,14,18]
int pre=nums[0];
nums[0]=0;
for(int k=1;k<T.nu;k++)
{
int t=nums[k];
nums[k]=pre+nums[k-1];
pre=t;;
}
//开始转置
for(int k=0;k<T.tu;k++)
{
int index=nums[T.elem[k].j];//转置后的位置
T1.elem[index].i=T.elem[k].j;
T1.elem[index].j=T.elem[k].i;
T1.elem[index].val=T.elem[k].val;
nums[T.elem[k].j]++;//下一次同一列的位置要往后移
}
T1.tu=T.tu;
}输出
void ShowTriplet(SqTriplet T)
{//展示三元组
cout<<"行 列 值\n";
for(int k=0;k<T.tu;k++)
{
cout<<T.elem[k].i<<" "<<T.elem[k].j<<" "<<T.elem[k].val<<endl;
}
}
void ShowMat(SqTriplet T)
{
int pos=0;
for(int row=0;row<T.mu;row++)
{
for(int col=0;col<T.nu;col++)
{
if(T.elem[pos].i==row&&T.elem[pos].j==col)
{ cout<<T.elem[pos].val<<" ";pos++;}
else cout<<"0 ";
}
cout<<endl;
}
}程序完整代码:
#include<iostream>
using namespace std;
typedef struct{
int i,j;
int val;
}Triplet;
typedef struct{
Triplet *elem;
int tu,mu,nu;//个数,行数,列数
}SqTriplet;
bool InitTriplet(SqTriplet &T,int rowSize,int colSize)
{
T.elem=new Triplet[rowSize*colSize/5];
if(!T.elem) return false;
T.tu=0;
T.mu=rowSize;
T.nu=colSize;
return true;
}
void compress(int M[][10],SqTriplet &T,int rowSize,int colSize)
{//压缩函数
for(int row=0;row<rowSize;row++)
{
for(int col=0;col<colSize;col++)
{
if(M[row][col]!=0)
{//非零项赋值,个数加一
// T.(elem+T.length)->row=i;
T.elem[T.tu].i=row;
T.elem[T.tu].j=col;
T.elem[T.tu].val=M[row][col];
T.tu++;
}
}
}
}
void reserve(SqTriplet T,SqTriplet &T1)
{//T转置==>T1
//记录每一列元素的个数
int nums[T.nu]={0};
for(int k=0;k<T.tu;k++)
{
nums[T.elem[k].j]++;
}
//记录每一列之前的列一共有多少个数据[1,3,5,2,3,4,5]
// nums[i] =[0,i-1]列元素个数 [0,1,4,9,11,14,18]
int pre=nums[0];
nums[0]=0;
for(int k=1;k<T.nu;k++)
{
int t=nums[k];
nums[k]=pre+nums[k-1];
pre=t;;
}
//开始转置
for(int k=0;k<T.tu;k++)
{
int index=nums[T.elem[k].j];//转置后的位置
T1.elem[index].i=T.elem[k].j;
T1.elem[index].j=T.elem[k].i;
T1.elem[index].val=T.elem[k].val;
nums[T.elem[k].j]++;//下一次同一列的位置要往后移
}
T1.tu=T.tu;
}
void ShowTriplet(SqTriplet T)
{//展示三元组
cout<<"行 列 值\n";
for(int k=0;k<T.tu;k++)
{
cout<<T.elem[k].i<<" "<<T.elem[k].j<<" "<<T.elem[k].val<<endl;
}
}
void ShowMat(SqTriplet T)
{
int pos=0;
for(int row=0;row<T.mu;row++)
{
for(int col=0;col<T.nu;col++)
{
if(T.elem[pos].i==row&&T.elem[pos].j==col)
{ cout<<T.elem[pos].val<<" ";pos++;}
else cout<<"0 ";
}
cout<<endl;
}
}
int main()
{
int m,n;
SqTriplet T,Ta;
cout<<"输入矩阵的行数和列数:\n";
cin>>m>>n;
cout<<"请输入矩阵:\n";
int M[10][10];
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
cin>>M[i][j];
//压缩
InitTriplet(T,m,n);
compress(M,T,m,n);
cout<<"压缩后的三元组:\n";
ShowTriplet(T);
//转置
InitTriplet(Ta,m,n);
reserve(T,Ta);
ShowTriplet(Ta);
//根据三元组来输出矩阵
cout<<"转置后的矩阵:\n";
ShowMat(Ta);
}测试: