1. 路径规划算法总体介绍

    Apollo中对路径规划解耦，分为路径规划与速度规划两部分。并将规划分为决策与优化两个部分。
• 路径规划 —— 静态环境（道路，静止/低速障碍物）
• 速度规划 —— 动态环境（中/高速障碍物）

    路径规划的配置文件在lane_follow_config.pb.txt中

// /home/yuan/apollo-edu/modules/planning/conf/scenario/lane_follow_config.pb.txt

scenario_type: LANE_FOLLOW
stage_type: LANE_FOLLOW_DEFAULT_STAGE
stage_config: {
//路径规划
  stage_type: LANE_FOLLOW_DEFAULT_STAGE
  enabled: true
  task_type: LANE_CHANGE_DECIDER
  task_type: PATH_REUSE_DECIDER
  task_type: PATH_LANE_BORROW_DECIDER
  task_type: PATH_BOUNDS_DECIDER
  task_type: PIECEWISE_JERK_PATH_OPTIMIZER
 //速度规划 
  task_type: PATH_ASSESSMENT_DECIDER
  task_type: PATH_DECIDER
  task_type: RULE_BASED_STOP_DECIDER
  task_type: SPEED_BOUNDS_PRIORI_DECIDER
  task_type: SPEED_HEURISTIC_OPTIMIZER
  task_type: SPEED_DECIDER
  task_type: SPEED_BOUNDS_FINAL_DECIDER
  task_type: PIECEWISE_JERK_SPEED_OPTIMIZER
  # task_type: PIECEWISE_JERK_NONLINEAR_SPEED_OPTIMIZER
  task_type: RSS_DECIDER

_DECIDER结尾的为决策部分 _OPTIMIZER结尾的为优化部分。

1.1 Task： LANE_CHANGE_DECIDER

产生是否换道的决策，更新换道状态

    首先判断是否产生多条参考线，若只有一条参考线，则保持直行。若有多条参考线，则根据一些条件（主车的前方和后方一定距离内是否有障碍物，旁边车道在一定距离内是否有障碍物）进行判断是否换道，当所有条件都满足时，则进行换道决策。

1.2 Task： PATH_REUSE_DECIDER

路径是否可重用,提高帧间平顺性
    主要判断是否可以重用上一帧规划的路径。若上一帧的路径未与障碍物发生碰撞，则可以重用，提高稳定性，节省计算量。若上一帧的规划出的路径发生碰撞，则重新规划路径。

1.3 Task： PATH_BORROW_DECIDER

产生是否借道的决策

    该决策有以下的判断条件：
• 是否只有一条车道
• 是否存在阻塞道路的障碍物
• 阻塞障碍物是否远离路口
• 阻塞障碍物长期存在
• 旁边车道是实线还是虚线
    当所有判断条件都满足时，会产生借道决策。

1.4 Task： PATH_BOUNDS_DECIDER

产生路径边界

    利用前几个决策器，根据相应条件，产生相应的SL边界。这里说明以下Nudge障碍物的概念——主车旁边的障碍物未完全阻挡主车，主车可以通过绕行避过障碍物（注意图中的边界）。

1.5 Task： PIECEWISE_JERK_PATH_OPTIMIZER

基于二次规划算法，对每个边界规划出最优路径.

1.6 Task： PATH_ASSESSMENT_DECIDER

路径评价，选出最优路径
    依据以下规则，进行评价。
路径是否和障碍物碰撞
路径长度
路径是否会停在对向车道
路径离自车远近
哪个路径更早回自车道
…
    路径两两进行对比，选出最优的路径。

1.7 Task： PATH_DECIDER

根据选出的路径给出对障碍物的决策
    若是绕行的路径，则产生绕行的决策；若前方有障碍物阻塞，则产生停止的决策。

2. 基于二次规划的路径规划算法

2.1 二次规划问题标准型

    牛津大学推出过二次规划的求解器，支持C/C++、python、Matlab等多种语言。
    二次规划问题的标准形式为：$$\begin{array}{ll}\mathrm{minimize}& \frac{1}{2}{x}^{T}Px+q^{T}x\\ \mathrm{subjectto}& l\le Ax\le u\end{array}$$    where $x\in {\mathbf{R}}^n$ is the optimization variable. The objective function is defined by a positive semidefinite matrix $P\in {\mathbf{S}}_{+}^n$and vector $q\in {\mathbf{R}}^n$ . The linear constraints are defined by matrix $A\in {\mathbf{R}}^{m\times n}$ and vectors $l$ and $u$ so that l i ∈ R ∪ { − ∞ } {l_i} \in {\bf{R}} \cup \{ - \infty \} li​∈R∪{−∞} and ‘ u i ∈ R ∪ { + ∞ } {`u_i} \in {\bf{R}} \cup \{ + \infty \} ‘ui​∈R∪{+∞} for all i ∈ { 1 , … , m } i \in \{ 1, \ldots ,m{\rm{\} }} i∈{1,…,m} .
    二次规划优化问题为二次型，其约束为线性型。$x$是要优化的变量，是一个$n$维的向量。$p$是二次项系数，是正定矩阵。$q$是一次项系数，是$n$维向量。$A$是一个$m$x$n$的矩阵，$A$为约束函数的一次项系数，$m$为约束函数的个数。$l$和$u$分别为约束函数的下边界和上边界。

常用二次规划求解器：

• OSQP :使用ADMM方法求解。 对于规模大的，含有大量等式或不等式约束的问题有较好的求解效率。
• qpOASES: 用可行域法，对于约束较少的小规模问题，qpOASES求解更快。

    二次规划问题的求解往往有以下几个步骤：定义目优化变量、设计目标函数、设计约束、求解器求解等几个步骤。

2.2 定义优化变量

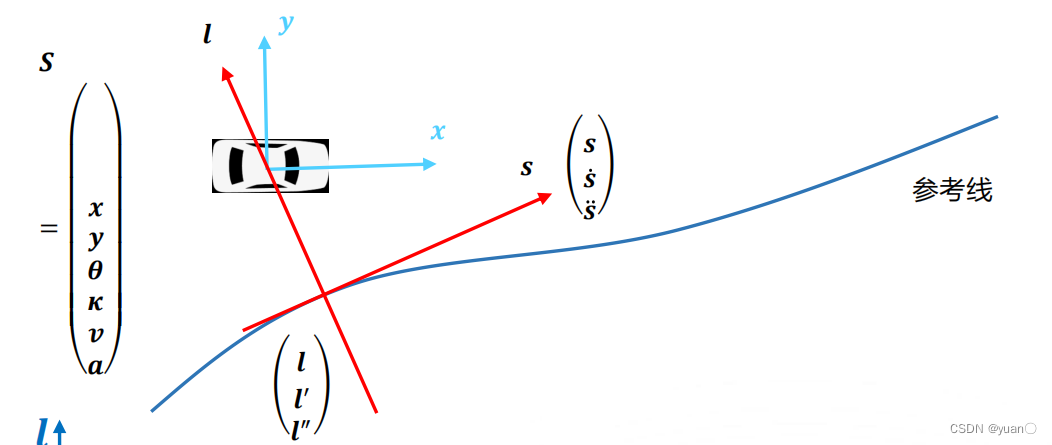    路径规划一般是在Frenet坐标系中进行的。$s$为沿着参考线的方向，$l$为垂直于坐标系的方向。    如图所示，将障碍物分别投影到SL坐标系上。在$s$方向上，以间隔$\Delta s$作为一个间隔点，从$s_0$,$s_1$,$s_2$一直到$s_{n-1}$，构成了规划的路径。选取每个间隔点的$l$作为优化的变量，同时也将$\dot{l}$和$\ddot{l}$也作为优化变量。
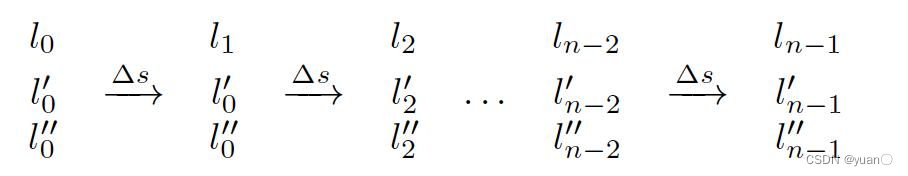    如此，就构成了优化变量$x$，$x$有三个部分组成：从$l_0$,$l_1$,$l_2$到$l_{n-1}$，从${\dot{l}}_0$,${\dot{l}}_1$,${\dot{l}}_2$到${\dot{l}}_{n-1}$,从${\ddot{l}}_0$,${\ddot{l}}_1$,${\ddot{l}}_2$到${\ddot{l}}_{n-1}$.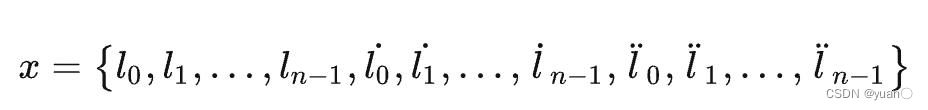

2.3 设计目标函数

    对于目标函数的设计，我们需要明确以下目标：

• 确保安全、礼貌的驾驶，尽可能贴近车道中心线行驶：$\left|l_i\right|\downarrow$
• 确保舒适的体感，尽可能降低横向速度/加速度/加加速度：$\left|{\dot{l}}_i\right|\downarrow$，$\left|{\ddot{l}}_i\right|\downarrow$，$\left|{l^{\prime \prime \prime }}_{i\to i+1}\right|\downarrow$
• 确保终点接近参考终点（这个往往用在靠边停车场景之中国）：$l_{end}=l_{ref}$

    最后会得到以下目标函数：
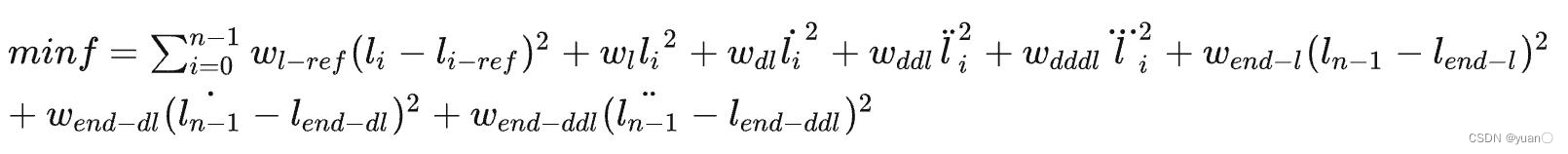    对每个点设计二次的目标函数并对代价值进行求和，式中的$w_l,w_{dl},w_{ddl},w_{dddl}$都是对于优化变量的惩罚项，以及偏移终点的惩罚项$w_{end-l},w_{end-dl},w_{end-ddl},w_{end-dddl}$。

ps：三阶导的求解方式为：$\frac{{l^{\prime \prime }}_{i+1}-{l^{\prime \prime }}_i}{\Delta s}$
    按照二次型的标准型，将目标函数的二次项系数和一次项系数用矩阵表示：$$\begin{array}{ll}\mathrm{minimize}& \frac{1}{2}{x}^{T}Px+q^{T}x\\ \mathrm{subjectto}& l\le Ax\le u\end{array}$$

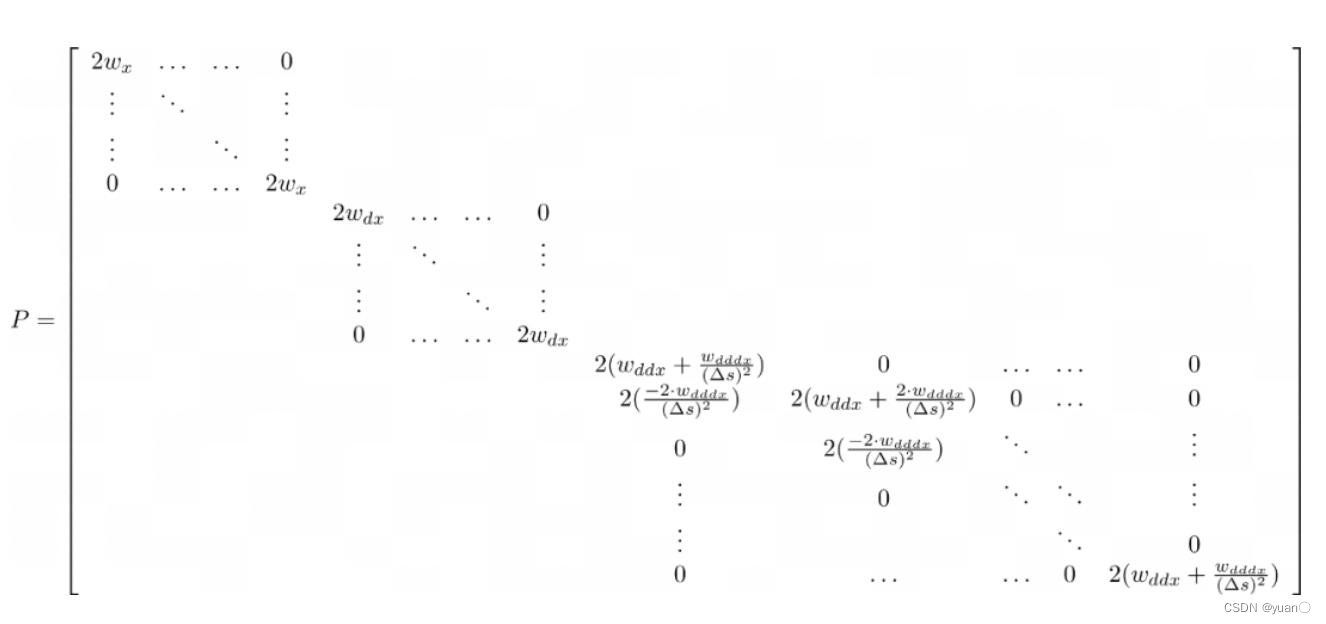
2.4 设计约束

    接下来谈谈约束的设计。
    约束要满足：
• 主车必须在道路边界内，同时不能和障碍物有碰撞$$l_i\in (l_{\min }^i,l_{\max }^i)$$    边界的约束已经在1.4 Task： PATH_BOUNDS_DECIDER里讲述过了。
• 根据当前状态，主车的横向速度/加速度/加加速度有特定运动学限制：
    首先是曲率的约束，车辆在行驶时有最大曲率半径的限制，根据Frenet坐标的转换公式（该公式来源于这篇论文——Werling M, Ziegler J, Kammel S, et al. Optimal trajectory generation for dynamic street scenarios in a frenet frame[C]//2010 IEEE International Conference on Robotics and Automation. IEEE, 2010: 987-993.）：    $l$的二阶导于曲率有如上关系，但我们无法直接将其应用于约束的设计（约束函数为一次）之中，对此需要对其进行简化。
假设1：参考线规划：$\theta -{\theta }_{ref}=\Delta \theta \approx 0$，即航向角几乎为0.
假设2：规划的曲率数值上很小，所以两个曲率相乘近乎为0.$$0<{\kappa }_{ref}<\kappa \ll 1\to {\kappa }_{ref}\kappa \approx 0$$    依据上述假设，我们将上述关系简化为：$$\frac{d^{2}l}{d{s}^2}=\kappa -{\kappa }_{ref}$$    根据车辆运动学关系计算最大曲率：$${\kappa }_{\max }=\frac{\tan ({\alpha }_{\max })}{L}$$    得到$\ddot{l}$的约束范围：$$-{\kappa }_{\max }-{\kappa }_{ref}<{\ddot{l}}_i<{\kappa }_{\max }-{\kappa }_{ref}$$    另外还得满足曲率变化率的要求（即规划处的路径能使方向盘在最大角速度下能够及时的转过来）：$$\frac{d^{3}l}{d{s}^3}=\frac{d\frac{d^{2}t}{d{l}^2}}{dt}\cdot \frac{dt}{ds}$$    主路行驶中，实际车轮转角很小$\alpha \to 0$，近似有$tan\alpha \approx \alpha$,从而有：$$\frac{d^{2}l}{d{s}^2}\approx \kappa -{\kappa }_{ref}=\frac{\tan ({\alpha }_{\max })}{L}-{\kappa }_{ref}\approx \frac{\alpha }{L}-{\kappa }_{ref}$$    同时假设，在一个周期内规划的路径上车辆的速度是恒定的$$v=\frac{dt}{ds}$$    代入三阶导公式得到三阶导的边界$$\frac{d^{3}l}{d{s}^3}=\frac{{\alpha }^{\prime }}{Lv}<\frac{{{\alpha }^{\prime }}_{\max }}{Lv}$$

总结

• 必须在道路边界内，同时不能和障碍物有碰撞$$l_i\in (l_{\min }^i,l_{\max }^i)$$
• 根据当前状态，主车的横向速度/加速度/加加速度有特定运动学限制：

• 必须满足基本的物理原理：

    三阶导$l^{\prime \prime \prime }$可以积成二阶导$l^{\prime \prime }$，二阶导$l^{\prime \prime }$可以积成一阶导$l^{\prime }$,一阶导$l^{\prime }$可以积成$l$。三阶导$l^{\prime \prime \prime }$为常量，二阶导$l^{\prime \prime }$，一阶导$l^{\prime }$，$l$为连续可导的。每个点之间都是三界多项的关系。
    将上述内容转化为约束矩阵。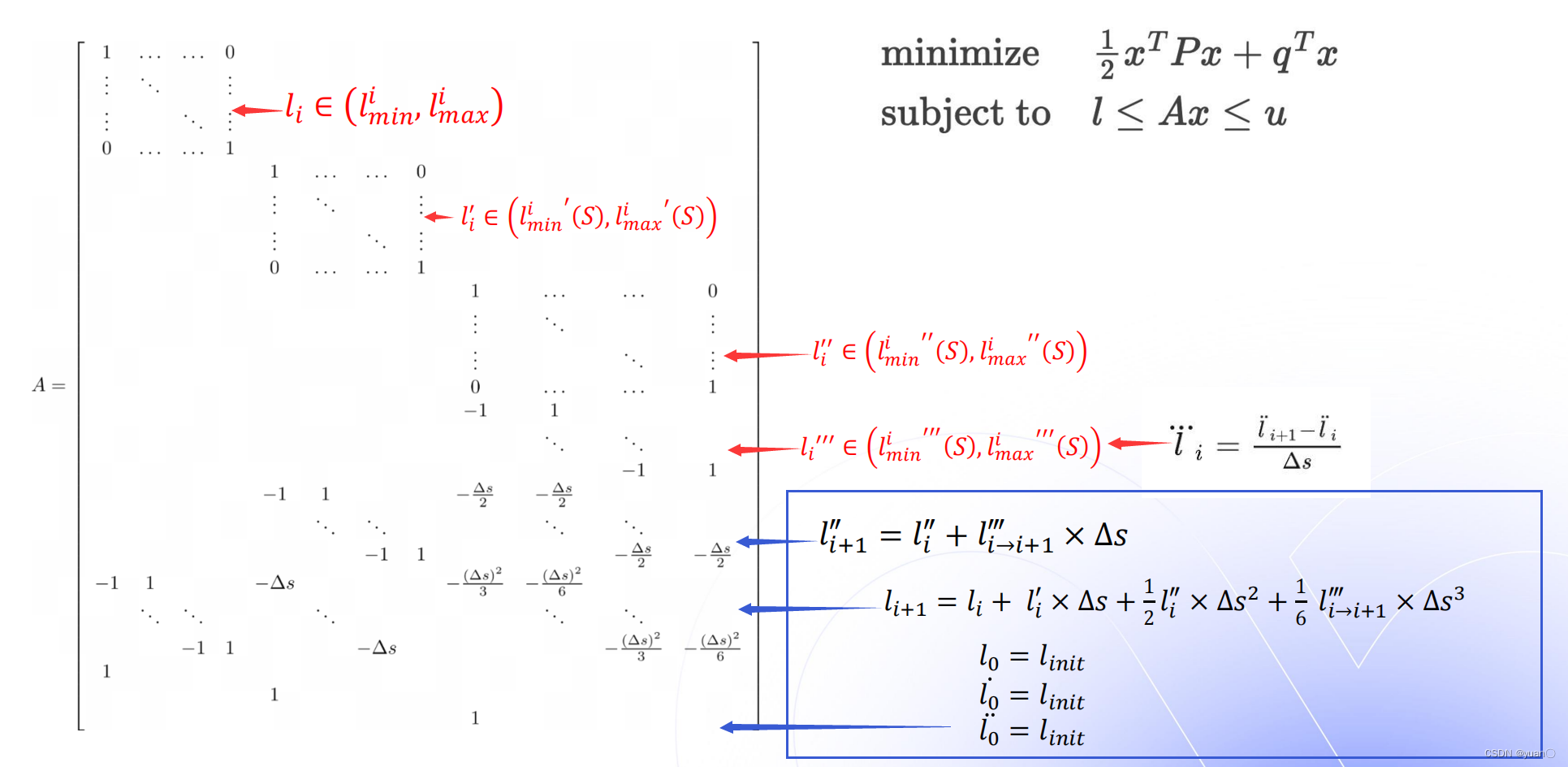    $l_0=l_{init}$,${\dot{l}}_0=l_{init}$,${\ddot{l}}_0=l_{init}$满足的是起点的约束，即为实际车辆规划起点的状态。

2.5 求解器求解

    最后是运用求解器进行求解。求解器求解同样需要四个步骤：设定OSQP求解参数、计算QP系数矩阵、构造OSQP求解器、获取优化结果。

2.5.1 设定OSQP求解参数

// /home/yuan/apollo-edu/modules/planning/math/piecewise_jerk/piecewise_jerk_speed_problem.cc
OSQPSettings* PiecewiseJerkSpeedProblem::SolverDefaultSettings() {
  // Define Solver default settings
  OSQPSettings* settings =
      reinterpret_cast<OSQPSettings*>(c_malloc(sizeof(OSQPSettings)));
  osqp_set_default_settings(settings);
  settings->eps_abs = 1e-4;
  settings->eps_rel = 1e-4;
  settings->eps_prim_inf = 1e-5;
  settings->eps_dual_inf = 1e-5;
  settings->polish = true;
  settings->verbose = FLAGS_enable_osqp_debug;
  settings->scaled_termination = true;

  return settings;
}

2.5.2 计算QP系数矩阵

// /home/yuan/apollo-edu/modules/planning/math/piecewise_jerk/piecewise_jerk_problem.cc
OSQPData* PiecewiseJerkProblem::FormulateProblem() {
  // calculate kernel
  std::vector<c_float> P_data;
  std::vector<c_int> P_indices;
  std::vector<c_int> P_indptr;
  CalculateKernel(&P_data, &P_indices, &P_indptr); // 二次项系数P的矩阵

  // calculate affine constraints
  std::vector<c_float> A_data;
  std::vector<c_int> A_indices;
  std::vector<c_int> A_indptr;
  std::vector<c_float> lower_bounds;
  std::vector<c_float> upper_bounds;
  CalculateAffineConstraint(&A_data, &A_indices, &A_indptr, &lower_bounds,
                            &upper_bounds); // 约束项系数A的矩阵

  // calculate offset
  std::vector<c_float> q;
  CalculateOffset(&q);   // 一次项系数q的向量

  OSQPData* data = reinterpret_cast<OSQPData*>(c_malloc(sizeof(OSQPData)));
  CHECK_EQ(lower_bounds.size(), upper_bounds.size());

  size_t kernel_dim = 3 * num_of_knots_;
  size_t num_affine_constraint = lower_bounds.size();

  data->n = kernel_dim;
  data->m = num_affine_constraint;
  data->P = csc_matrix(kernel_dim, kernel_dim, P_data.size(), CopyData(P_data),
                       CopyData(P_indices), CopyData(P_indptr));
  data->q = CopyData(q);
  data->A =
      csc_matrix(num_affine_constraint, kernel_dim, A_data.size(),
                 CopyData(A_data), CopyData(A_indices), CopyData(A_indptr));
  data->l = CopyData(lower_bounds);
  data->u = CopyData(upper_bounds);
  return data;
}

2.5.3 构造OSQP求解器

  OSQPWorkspace* osqp_work = nullptr;
  osqp_work = osqp_setup(data, settings);

2.5.4 获取优化结果

osqp_solve(osqp_work);

  auto status = osqp_work->info->status_val;// 获取优化值

  if (status < 0 || (status != 1 && status != 2)) {
    AERROR << "failed optimization status:\t" << osqp_work->info->status;
    osqp_cleanup(osqp_work);
    FreeData(data);
    c_free(settings);
    return false;
  } else if (osqp_work->solution == nullptr) {
    AERROR << "The solution from OSQP is nullptr";
    osqp_cleanup(osqp_work);
    FreeData(data);
    c_free(settings);
    return false;
  }

  // extract primal results
  x_.resize(num_of_knots_);
  dx_.resize(num_of_knots_);
  ddx_.resize(num_of_knots_);
  for (size_t i = 0; i < num_of_knots_; ++i) {
    x_.at(i) = osqp_work->solution->x[i] / scale_factor_[0];
    dx_.at(i) = osqp_work->solution->x[i + num_of_knots_] / scale_factor_[1];
    ddx_.at(i) =
        osqp_work->solution->x[i + 2 * num_of_knots_] / scale_factor_[2];
  } //优化变量的取值

  // Cleanup
  osqp_cleanup(osqp_work);
  FreeData(data);
  c_free(settings);
  return true;

3. 路径规划算法代码解读

3.1 总流程和决策\优化的入口函数

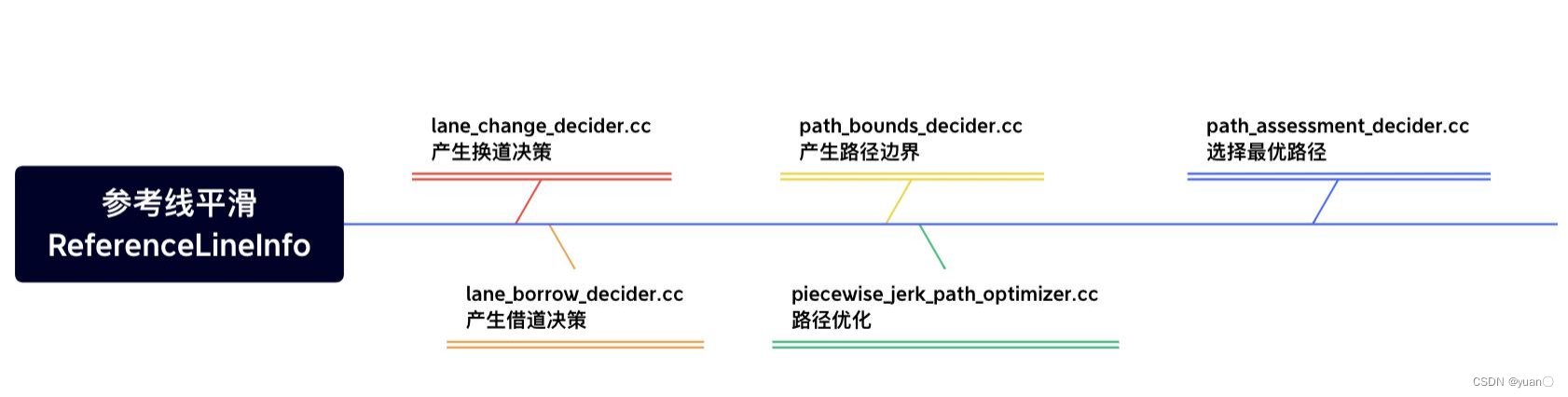    路径规划从参考线平滑开始，参考线模块结束后，会将中间计算结果保存在ReferenceLineinfo之中。之后按照路径规划的任务，依次执行上图中的任务。任务包括了决策器以及优化器的任务。

决策器的入口函数。输入每一帧的数据结构总类frame、参考线的中间计算结果current_reference_line_info到求解器中进行求解，最后结果保存在current_reference_line_info中。
优化器的入口函数。输入speed_data、reference_line、init_point、path_reusable、final_path_data等信息到求解器中求解，最后将结果保存在reference_line中。

3.2 产生换道决策

// /home/yuan/apollo-edu/modules/planning/tasks/deciders/lane_change_decider/lane_change_decider.cc
void LaneChangeDecider::UpdateStatus(double timestamp,
                                     ChangeLaneStatus::Status status_code,
                                     const std::string& path_id) {
  auto* lane_change_status = injector_->planning_context()
                                 ->mutable_planning_status()
                                 ->mutable_change_lane();
  lane_change_status->set_timestamp(timestamp);
  lane_change_status->set_path_id(path_id);
  lane_change_status->set_status(status_code);
}

    产生换道的状态，之后将结果保存在injector中。

3.3 产生借道决策

// /home/yuan/apollo-edu/modules/planning/tasks/deciders/path_lane_borrow_decider/path_lane_borrow_decider.cc
  // By default, don't borrow any lane.
  reference_line_info->set_is_path_lane_borrow(false);
  // Check if lane-borrowing is needed, if so, borrow lane.
  if (Decider::config_.path_lane_borrow_decider_config()
          .allow_lane_borrowing() &&
      IsNecessaryToBorrowLane(*frame, *reference_line_info)) {
    reference_line_info->set_is_path_lane_borrow(true);
  }

    当产生阶导决策时，会将相应标志位置true。

 if (!left_borrowable && !right_borrowable) {
        mutable_path_decider_status->set_is_in_path_lane_borrow_scenario(false);
        return false;
      } else {
        mutable_path_decider_status->set_is_in_path_lane_borrow_scenario(true);
        if (left_borrowable) {
          mutable_path_decider_status->add_decided_side_pass_direction(
              PathDeciderStatus::LEFT_BORROW);
        }
        if (right_borrowable) {
          mutable_path_decider_status->add_decided_side_pass_direction(
              PathDeciderStatus::RIGHT_BORROW);
        }
      }

    同时，在进行借道决策时，会对左右借道进行判断。借道的状态保存在injetor里。

3.4 产生路径边界

    根据现有决策在参考线上进行采样，获得每个点在$l$的边界。有四种边界决策：GenerateRegularPathBound（自车道行驶）、GenerateFallbackPathBound（失败回退）、GenerateLaneChangePathBound、GeneratePullOverPathBound。最后将边界保存在SetCandidatePathBoundaries中，供下一步使用。

3.5 路径优化

 piecewise_jerk_problem.set_x_ref(std::move(weight_x_ref_vec),
                                     path_reference_l_ref);
  }
  // for debug:here should use std::move
  piecewise_jerk_problem.set_weight_x(w[0]);
  piecewise_jerk_problem.set_weight_dx(w[1]);
  piecewise_jerk_problem.set_weight_ddx(w[2]);
  piecewise_jerk_problem.set_weight_dddx(w[3]);

  piecewise_jerk_problem.set_scale_factor({1.0, 10.0, 100.0});

  auto start_time = std::chrono::system_clock::now();

  piecewise_jerk_problem.set_x_bounds(lat_boundaries);
  piecewise_jerk_problem.set_dx_bounds(-FLAGS_lateral_derivative_bound_default,
                                       FLAGS_lateral_derivative_bound_default);
  piecewise_jerk_problem.set_ddx_bounds(ddl_bounds);

  // Estimate lat_acc and jerk boundary from vehicle_params
  const auto& veh_param =
      common::VehicleConfigHelper::GetConfig().vehicle_param();
  const double axis_distance = veh_param.wheel_base();
  const double max_yaw_rate =
      veh_param.max_steer_angle_rate() / veh_param.steer_ratio() / 2.0;
  const double jerk_bound = EstimateJerkBoundary(std::fmax(init_state[1], 1.0),
                                                 axis_distance, max_yaw_rate);
  piecewise_jerk_problem.set_dddx_bound(jerk_bound);

  bool success = piecewise_jerk_problem.Optimize(max_iter);

    调用piecewise_jerk_problem类进行求解，会设置一些权重以及一些约束，利用Optimize函数进行求解。

 const auto& path_boundaries =
      reference_line_info_->GetCandidatePathBoundaries();
  ADEBUG << "There are " << path_boundaries.size() << " path boundaries.";
  const auto& reference_path_data = reference_line_info_->path_data();

  std::vector<PathData> candidate_path_data;
  for (const auto& path_boundary : path_boundaries) {
    size_t path_boundary_size = path_boundary.boundary().size();

    reference_line_info_->GetCandidatePathBoundaries();保存候选路径。

 if (candidate_path_data.empty()) {
    return Status(ErrorCode::PLANNING_ERROR,
                  "Path Optimizer failed to generate path");
  }
  reference_line_info_->SetCandidatePathData(std::move(candidate_path_data));

3.6 选择最优路径

bool ComparePathData(const PathData& lhs, const PathData& rhs,
                     const Obstacle* blocking_obstacle) {
  ADEBUG << "Comparing " << lhs.path_label() << " and " << rhs.path_label();
  // Empty path_data is never the larger one.
  if (lhs.Empty()) {
    ADEBUG << "LHS is empty.";
    return false;
  }
  if (rhs.Empty()) {
    ADEBUG << "RHS is empty.";
    return true;
  }

     调用ComparePathData函数，对路径进行两两比较。

 *(reference_line_info->mutable_path_data()) = valid_path_data.front();
  reference_line_info->SetBlockingObstacle(
      valid_path_data.front().blocking_obstacle_id());

     将最优的路径保存在reference_line_info中。将阻塞障碍物最近的放在reference_line_info中，供速度规划进一步处理。

4. 路径规划算法实践

云实验地址——Apollo规划之路径规划仿真调试

4.1 观察借道绕行、自车道绕行障碍物、自车道巡航、换道时路径的边界和规划的路径

(1）在终端中输入以下指令，启动dreamview

 bash scripts/bootstrap_neo.sh 

(2）模式选择Mkz Standard Debug，地图选择Apollo Virutal Map，打开Sim_Control模式，打开PNC Monitor,等待屏幕中间区域出现Mkz车模型和地图后即表示成功进入仿真模式。
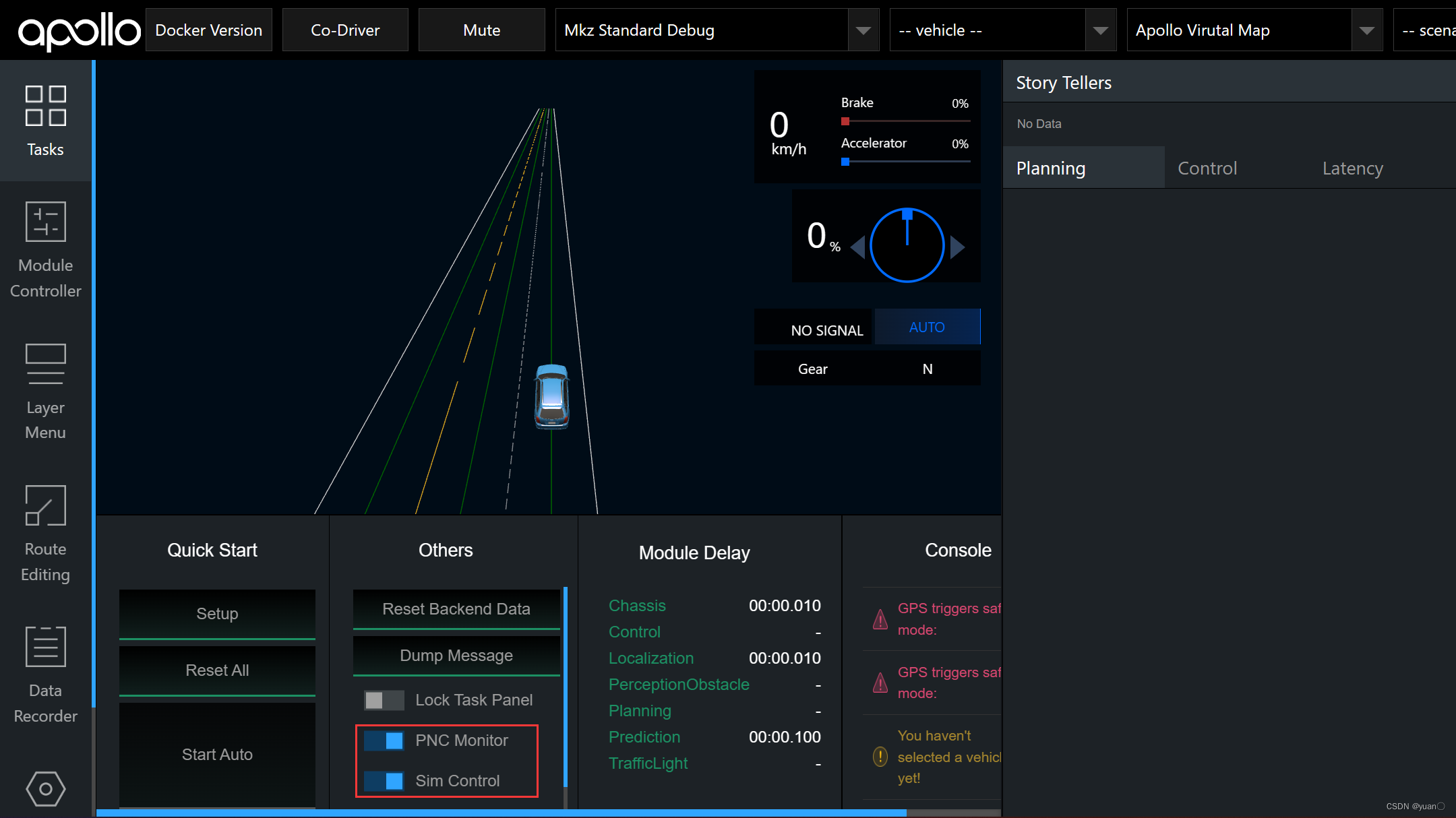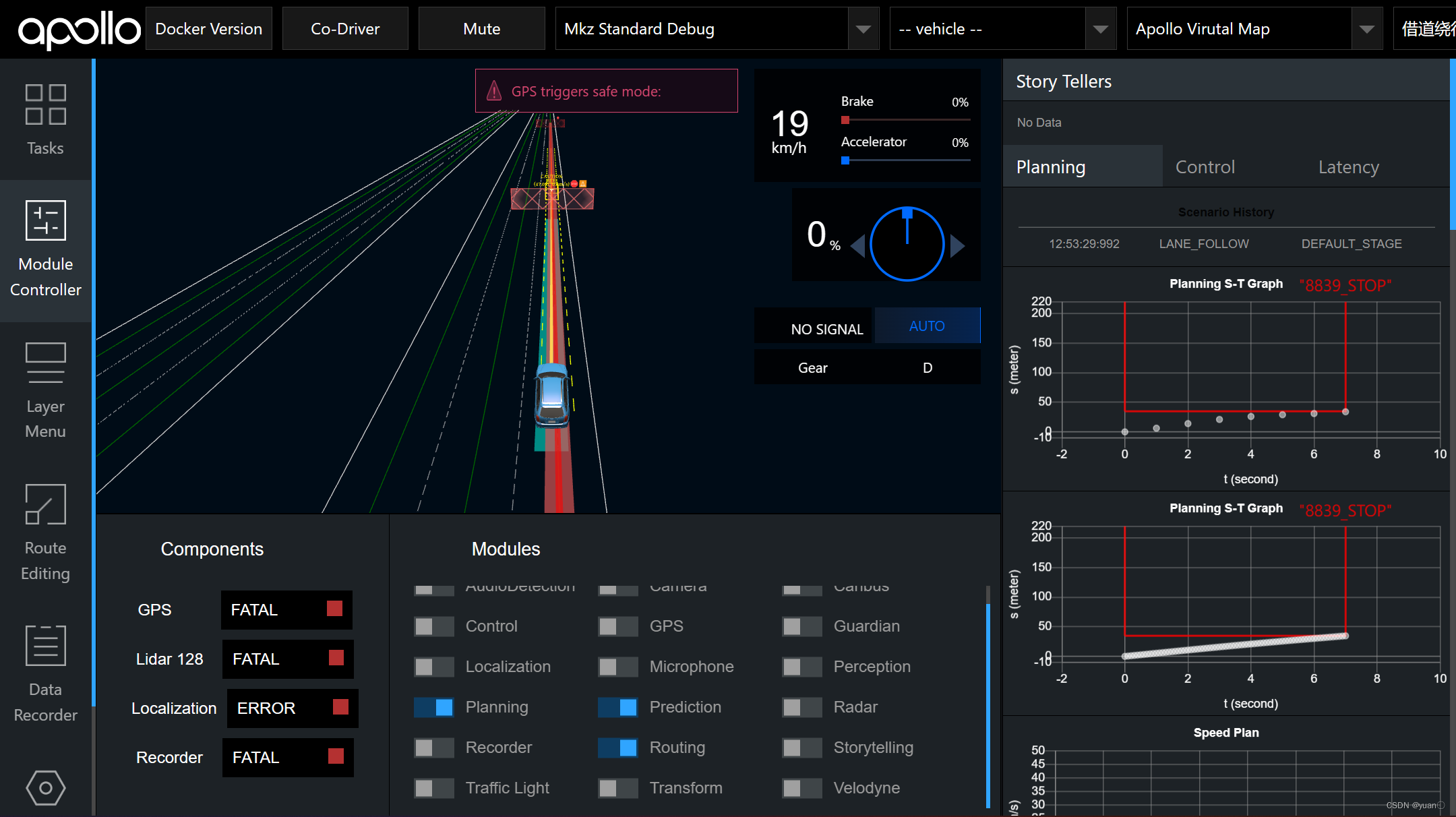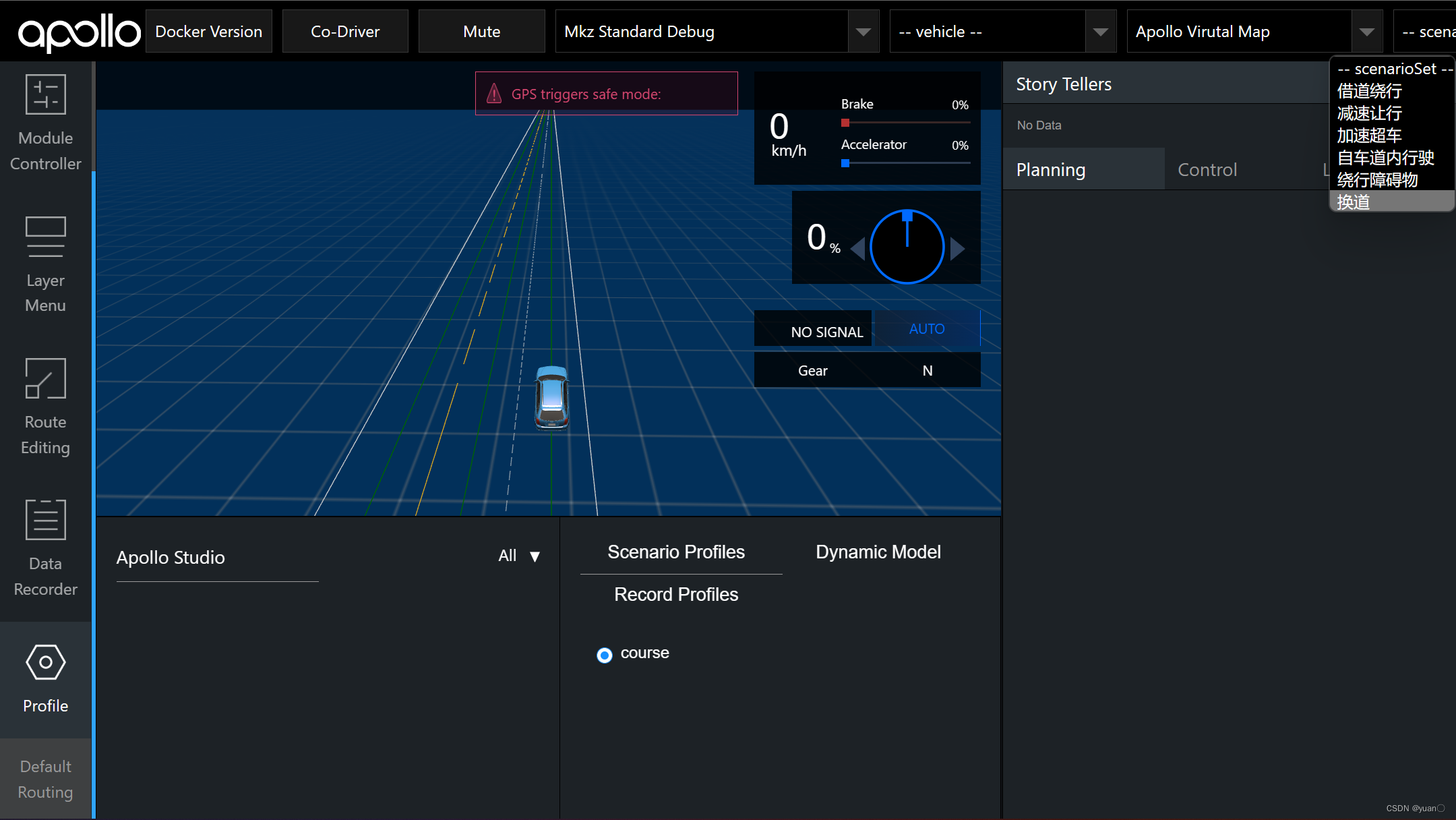
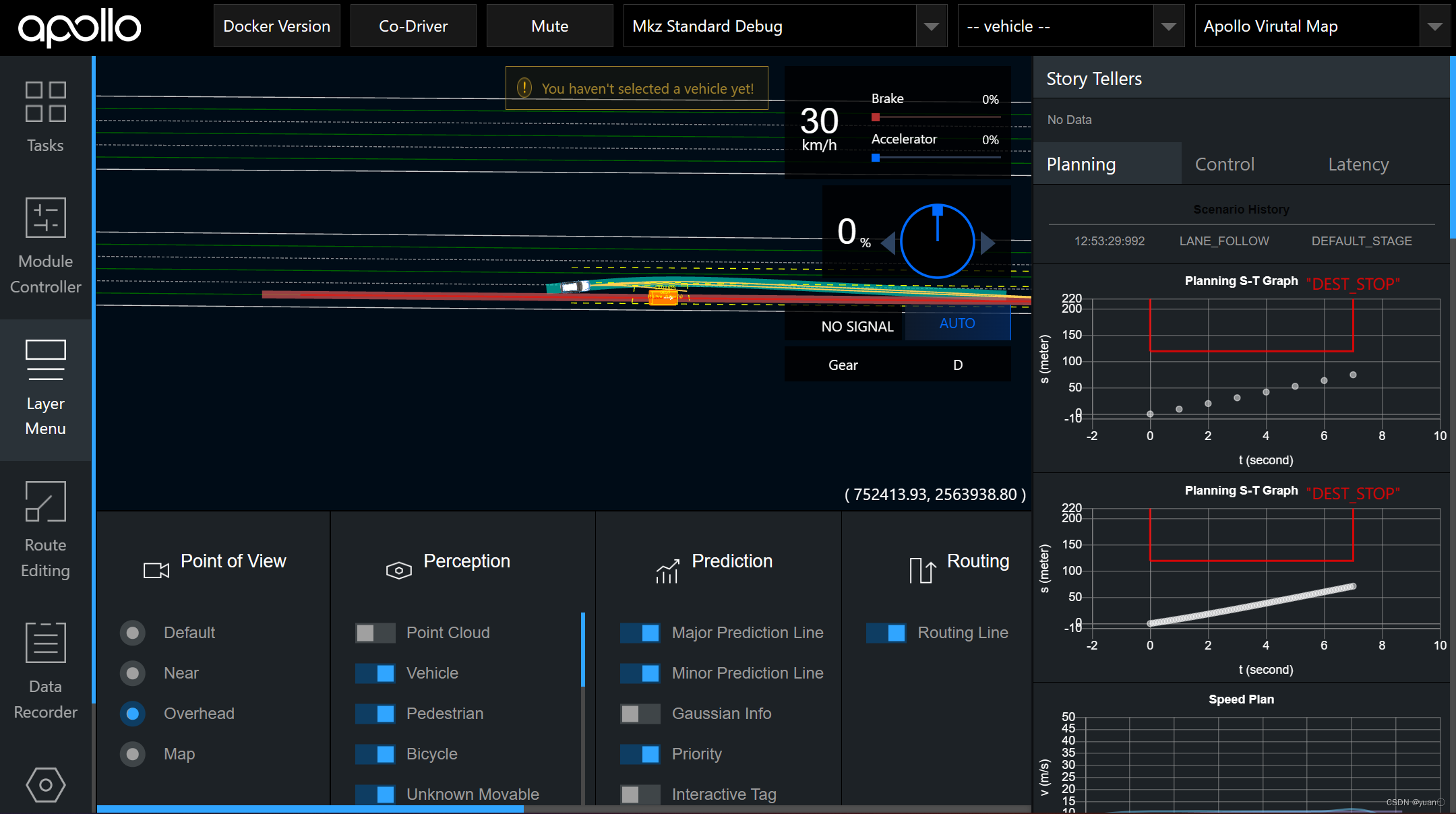
(3）点击左侧Tab栏Module Controller，启动Planning,Prediction，Routing模块，如果需要录制数据则打开Recorder模块。(4）模块启动完成后，点击左侧Tab栏Profile，选择Scenario Profiles里的course场景集，右上角选择场景场景开始仿真，分别点击自车道内行驶，绕行障碍物，借道绕行，换道场景。观察路径曲线和路径边界.Layer Menu中控制Planning的各个path和boundary开关可以显示和关闭每一条候选路径.

借道绕行
借道绕行
自车道行驶

自车道行驶
自车道绕行（Nudge障碍物）

自车道绕行（Nudge障碍物）
变道

变道

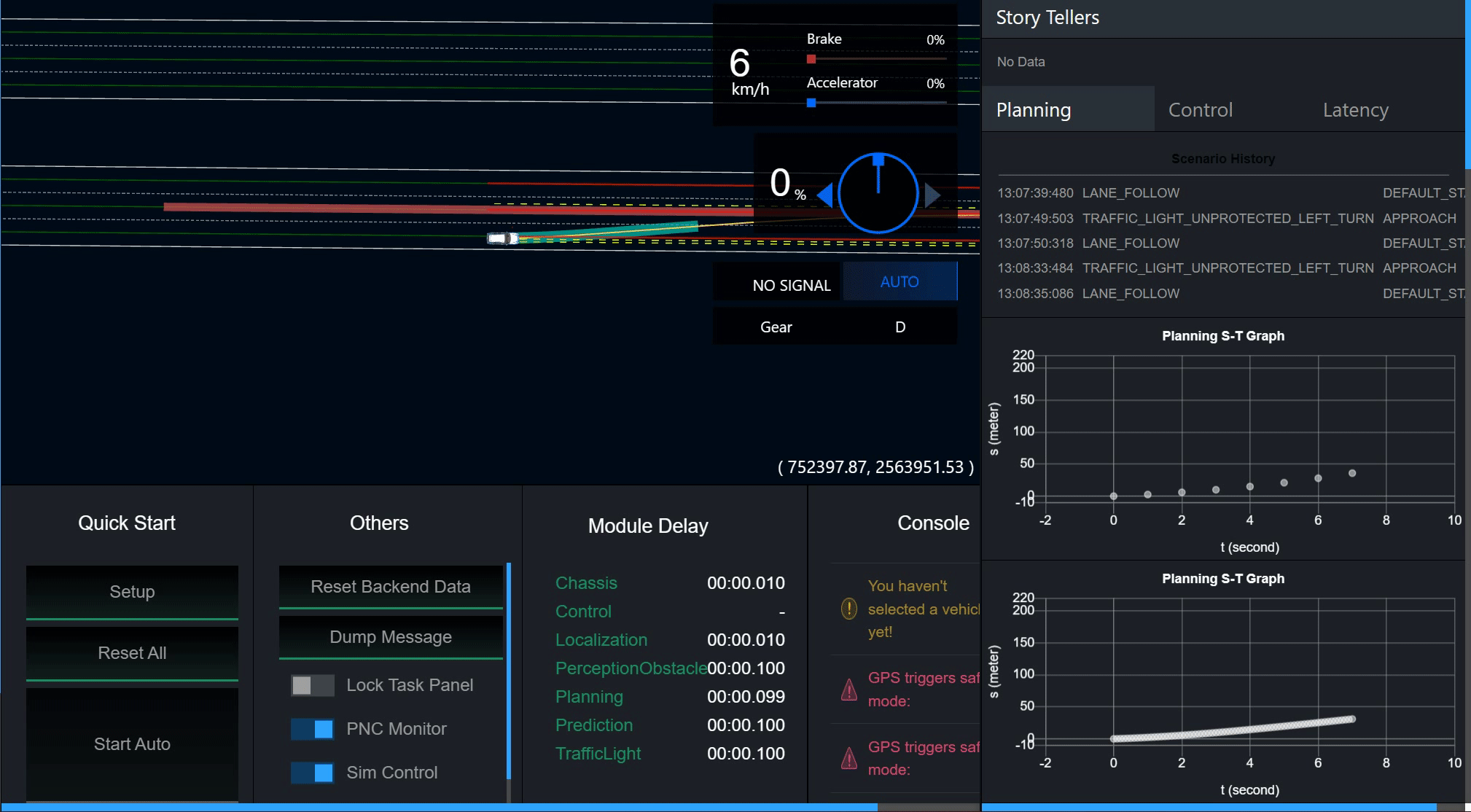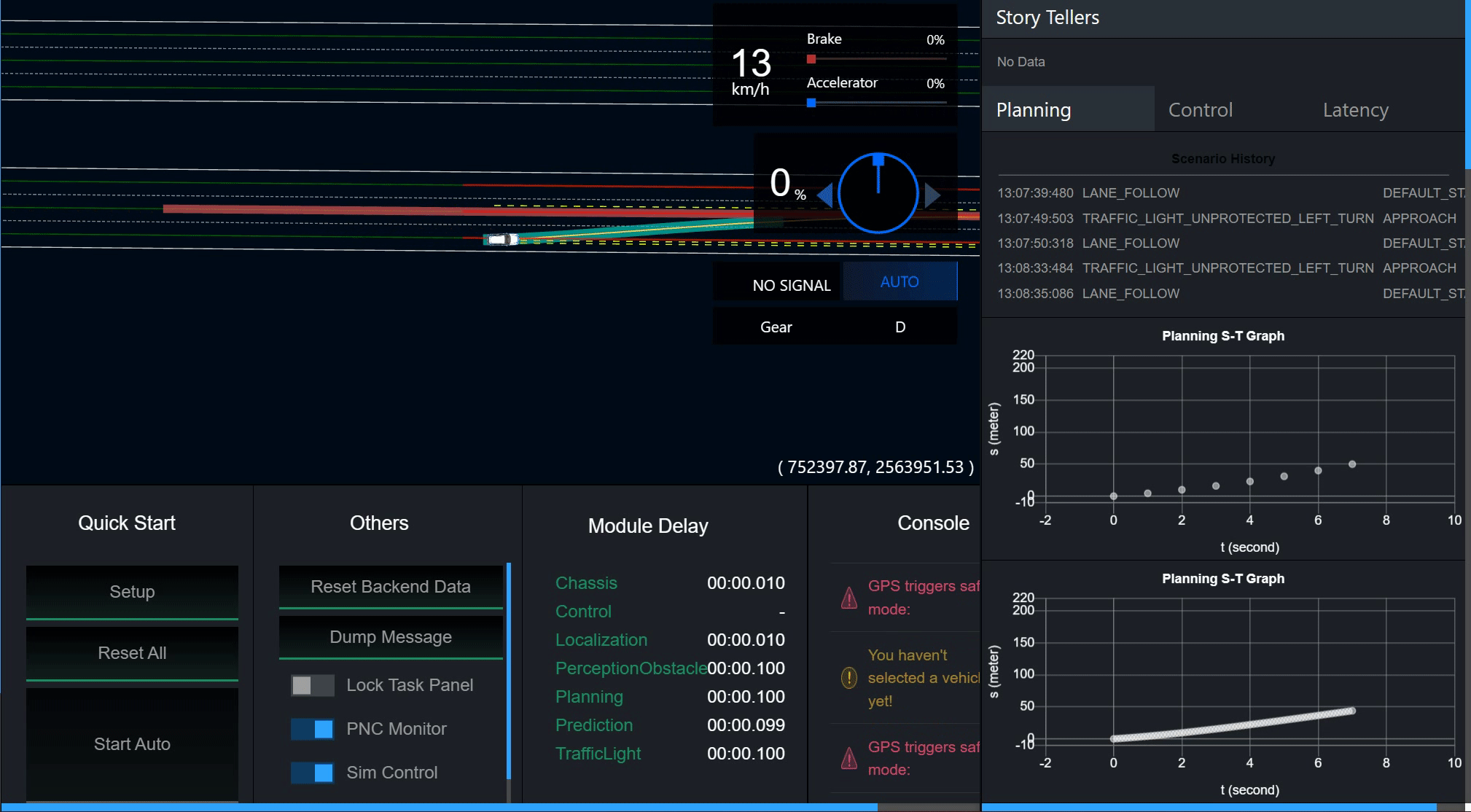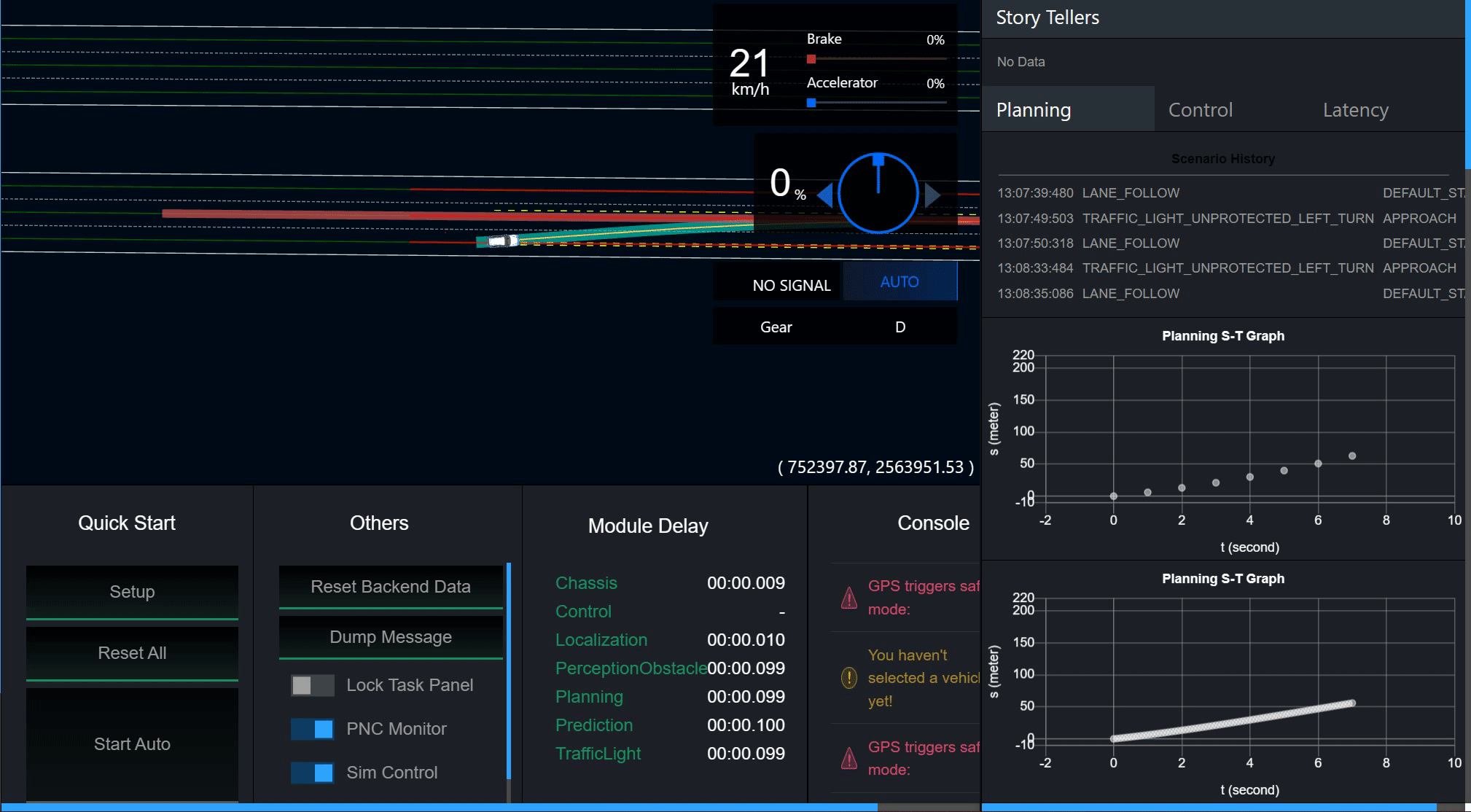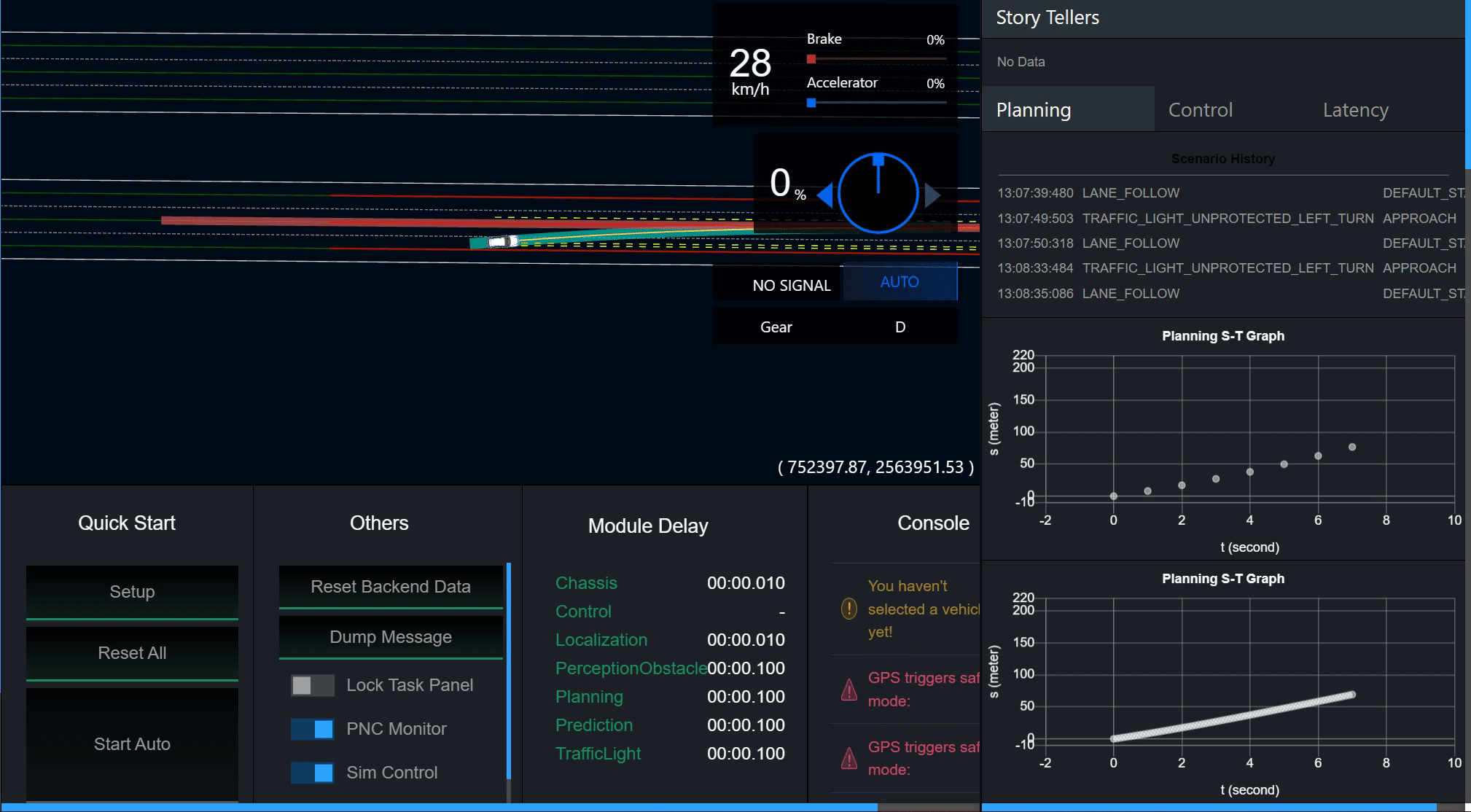
4.2 借道绕行场景，调整$l,l’,l’’$的权重系数，观察路径的变化

在modules/planning/conf/planning_config.pb.txt配置文件中，包含了路径规划任务的相关参数，我们可以过对这些参数的调整，达到我们期望路径规划效果。

(1)使用在线编辑工具修改/apollo/modules/planning/conf目录下的planning_config.pb.txt文件，增大default_path_config的l_weight，减小dl_weight ddl_weight dddl_weight。

default_task_config: {
  task_type: PIECEWISE_JERK_PATH_OPTIMIZER
  piecewise_jerk_path_optimizer_config {
    default_path_config {
      l_weight: 1.0
      dl_weight: 20.0
      ddl_weight: 1000.0
      dddl_weight: 50000.0
    }
    lane_change_path_config {
      l_weight: 1.0
      dl_weight: 5.0
      ddl_weight: 800.0
      dddl_weight: 30000.0
    }
  }
}

(2)修改好代码参数后，保存这个文件，在ModuleController中重启planning模块（必须步骤)。
(3）重新选择借道绕行场景，观察轨迹和调整前有何变化

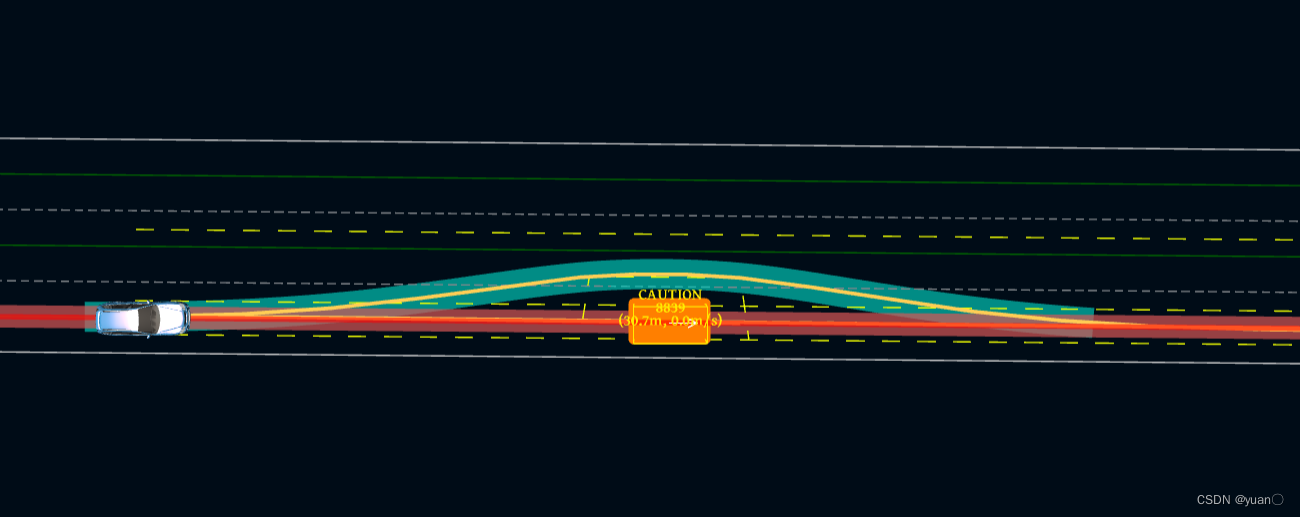
提前借道，提前回到原先车道，轨迹曲率更大。

4.3 靠边停车实践，开启靠边停车功能，观察路径的变化

恢复参数为默认值，在planning.conf中添加命令行参数–enable_scenario_pull_over=true，启动靠边停车，修改好代码参数后，保存这个文件，在Module Controller中重启planning模块（必须步骤）。
靠边停车目标点产生惩罚项使得规划出的轨迹偏离原参考线。