数组中数字出现的次数
- 一,有限状态自动机解法
- 二,一般解法
想必大家对数组中数字出现的次数的这种题并不少见,
主要有三种:
1,找出数组中只出现一次的数字(其他数字出现两次)
2,找出数组中仅有的两个仅出现一次的数字(其他数字出现两次)
3,找出数组中仅出现一次的数字(其他数字均出现三次)本次主要对第三个问题进行讲解,因为前两种的思路,很容易想出,且很好理解。
我把三道题的链接放到下面:
链接: 1,仅有一个数字出现一次
链接: 2,仅有两个数字出现一次
链接: 3,仅有一个数字出现一次,其余出现三次
一,有限状态自动机解法
大体的思路:
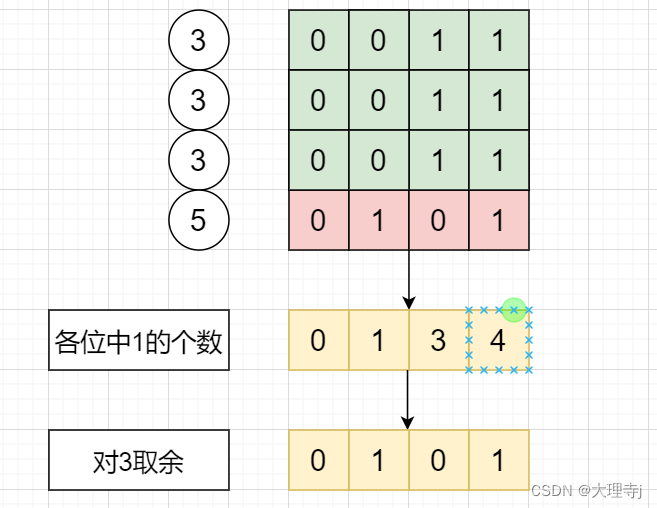
统计32个比特位中,每一位1的出现次数,将其对3取余,最终得到的结果就是仅出现一次的数字
由于二进制位的位运算规则相同,所以考虑一位即可。
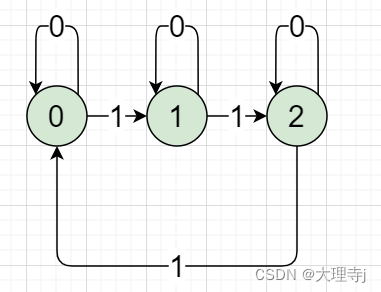
如下图所示,某二进制1的个数仅有三种状态:0,1,2
1,如果输入二进制位1,就按照以下做出转换。
2,如果输入二进制位0,不做转换。
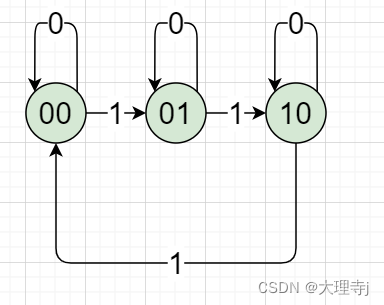
由于,每个比特位,不是0就是1,无法记录2,所以引出第二个状态位
分别将其命名:one two 表示两个状态位。
- 下面讲解如何对one ,two两个状态位进行更新
- 状态位 one的更新:
if(two==0)
{
if(n==1)
one=~one;
else
one=one;
}
else if(two==1)
{
one=0;
}
可以,对其用位操作符进行简化:
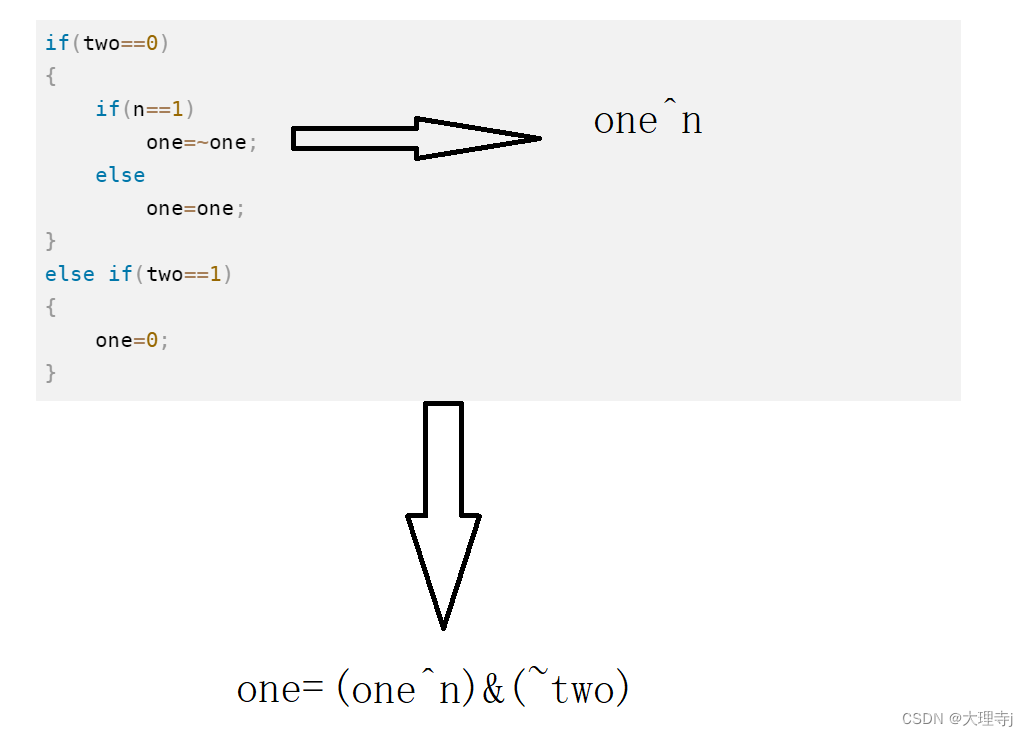
- 状态位two的更新:
状态two的更新是根据更新后的one来进行的(注意是更新后的one哟)
if(two==1)
{
if(n==1)
{
if(one==0)
two=0;
}
}
else if(two==0)
{
if(n==1)
{
if(one==0)
two=1;
}
}
为了方便理解,可以根据表格中的数据,理解上述关系式。
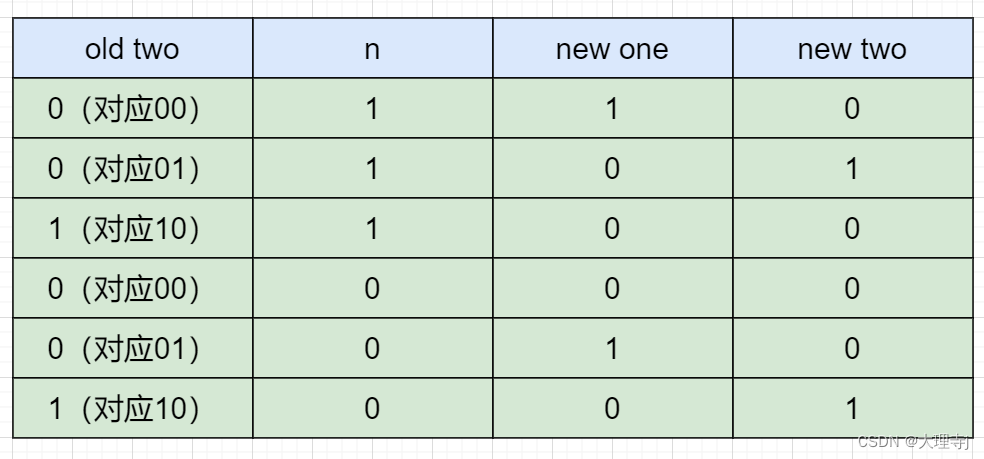
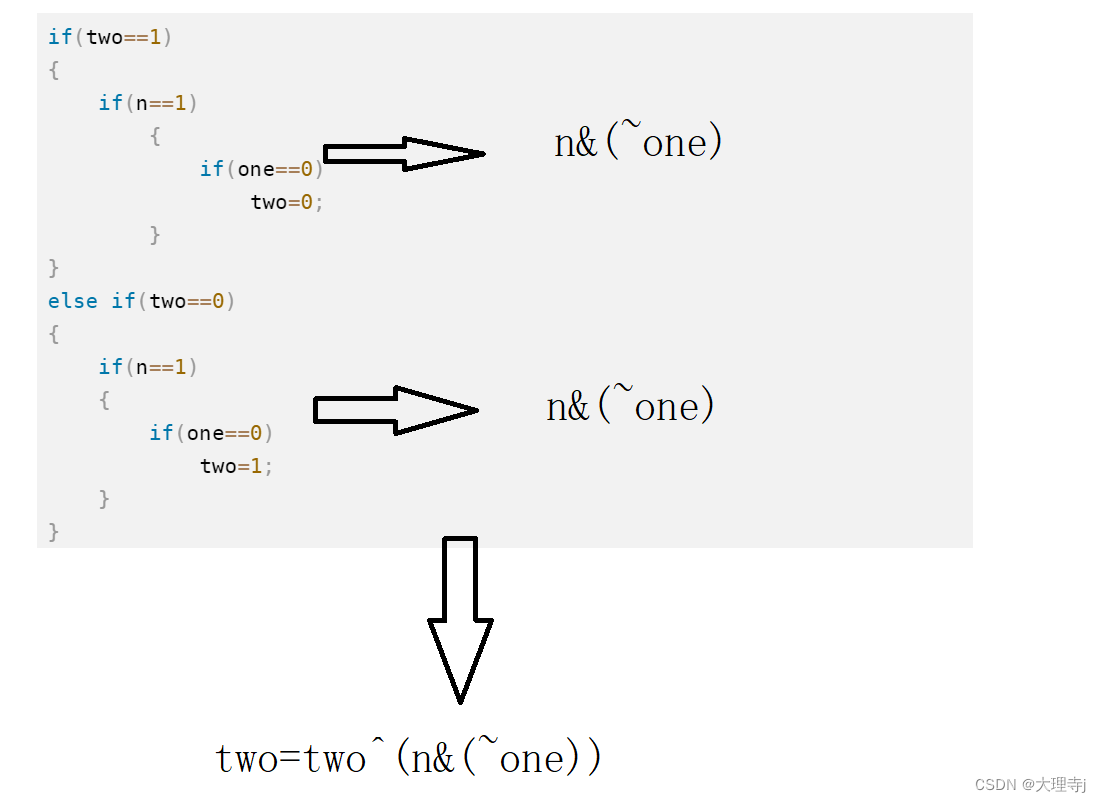
- 代码:
- 注意:&的优先级高于^
int singleNumber(int* nums, int numsSize){
int twos=0,ones=0;
for(int i=0;i<numsSize;i++)
{
ones = ones ^ nums[i] & ~twos;
twos = twos ^ nums[i] & ~ones;
}
return ones;
}
别看这代码只有短短的几行,但是这其中的思考量是不小的。
- 解释为何要做出简化:
因为如果按照上述那种if else语句写的话,只是针对某个比特位,而简化后是对整个数据而言(也就是32个比特位)。
二,一般解法
所谓一般解法,就是分别记录各个数据的每个比特位,然后每位的数量进行%3处理。
int singleNumber(int* nums, int numsSize){
int a[32]={0};
for(int i=0;i<numsSize;i++)
{
for(int j=0;j<32;j++)
{
a[j]+=nums[i]&1;
nums[i]>>=1;
}
}
int sum=0;
for(int i=0;i<32;i++)
{
sum+=a[i]%3==0?0:(int)pow(2,i);
}
return sum;
}
对比这种解法来说,更容易理解,且适用性很强,无论题目中其他数据都出现几次,我们只需该一处代码即可。但是效率不如上面的解法优秀。