题目

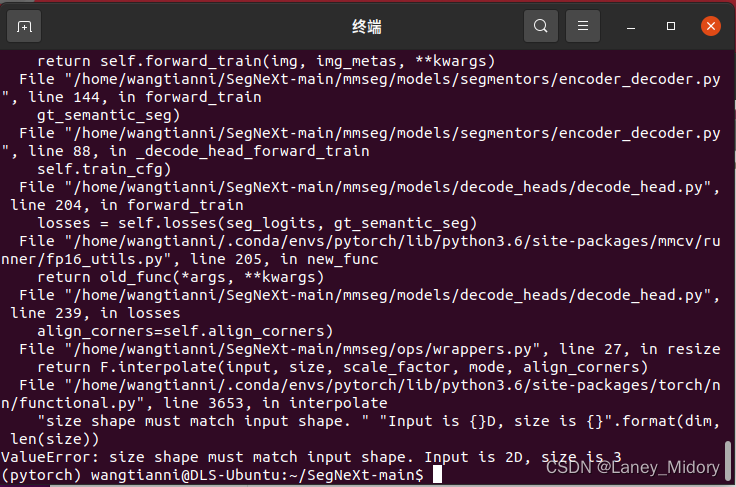
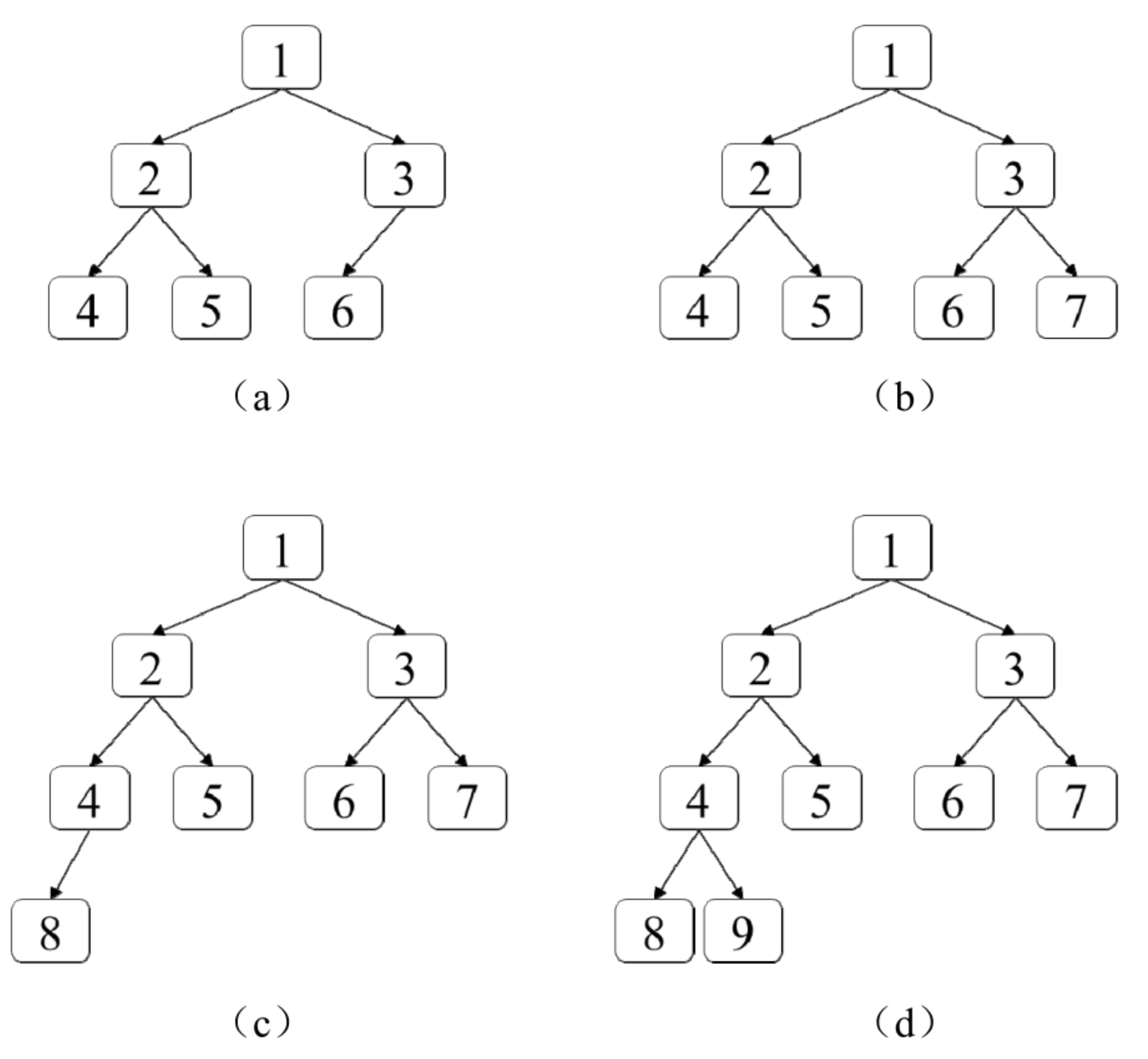
在完全二叉树中，除最后一层之外其他层的节点都是满的（第n层有2^n-1个节点）。最后一层的节点可能不满，该层所有的节点尽可能向左边靠拢。例如，图7.3中的4棵二叉树均为完全二叉树。实现数据结构CBTInserter有如下3种方法。

• 构造函数CBTInserter（TreeNode root），用一棵完全二叉树的根节点初始化该数据结构。
• 函数insert（int v）在完全二叉树中添加一个值为v的节点，并返回被插入节点的父节点。例如，在如图7.3（a）所示的完全二叉树中添加一个值为7的节点之后，二叉树如图7.3（b）所示，并返回节点3。在如图7.3（b）所示的完全二叉树中添加一个值为8的节点之后，二叉树如图7.3（c）所示，并返回节点4。在如图7.3（c）所示的完全二叉树中添加节点9会得到如图7.3（d）所示的二叉树并返回节点4。
• 函数get_root()返回完全二叉树的根节点。
  

分析

在完全二叉树中添加新节点顺序看起来是从上到下按层从左到右添加的，这就是典型的二叉树广度优先搜索的顺序。我们可以每次在完全二叉树中按照广度优先搜索的顺序找出第1个左子节点或右子节点还有空缺的节点。如果它没有左子节点，那么新的节点就作为它的左子节点；如果它没有右子节点，那么新的节点就作为它的右子节点。

接下来考虑效率优化。在完全二叉树中添加节点时需要按照广度优先搜索的顺序找出第1个缺少子节点的节点。其实没有必要在每次插入新的节点时都从完全二叉树的根节点开始从头进行广度优先搜索。

例如，在如图7.3（a）所示的完全二叉树中添加新的节点7时，从根节点开始按照广度优先搜索的顺序找出节点3是第1个缺少子节点的节点，由此可知，在节点3之前被遍历过的所有节点（节点1和节点2）的左右子节点都已经存在，并且当节点7插入节点3的右子节点的位置之后节点3的左右子节点都已经存在。下次再次插入新的节点时，就没有必要从根节点开始，而是跳过节点1、节点2和节点3，直接从节点4开始查找第1个还缺少子节点的节点。

解

public class CBTInserter {
    private Queue<TreeNode> queue;
    private TreeNode root;

    public CBTInserter(TreeNode root) {
        this.root = root;

        queue = new LinkedList<>();
        queue.offer(root);
        while (queue.peek().left != null && queue.peek().right != null) {
            TreeNode node = queue.poll();
            queue.offer(node.left);
            queue.offer(node.right);
        }
    }

    public int insert(int v) {
        TreeNode parent = queue.peek();
        TreeNode node = new TreeNode(v);

        if (parent.left == null) {
            parent.left = node;
        }
        else {
            parent.right = node;

            queue.poll();
            queue.offer(parent.left);
            queue.offer(parent.right);
        }

        return parent.val;
    }

    public TreeNode getRoot() {
        return this.root;
    }
}