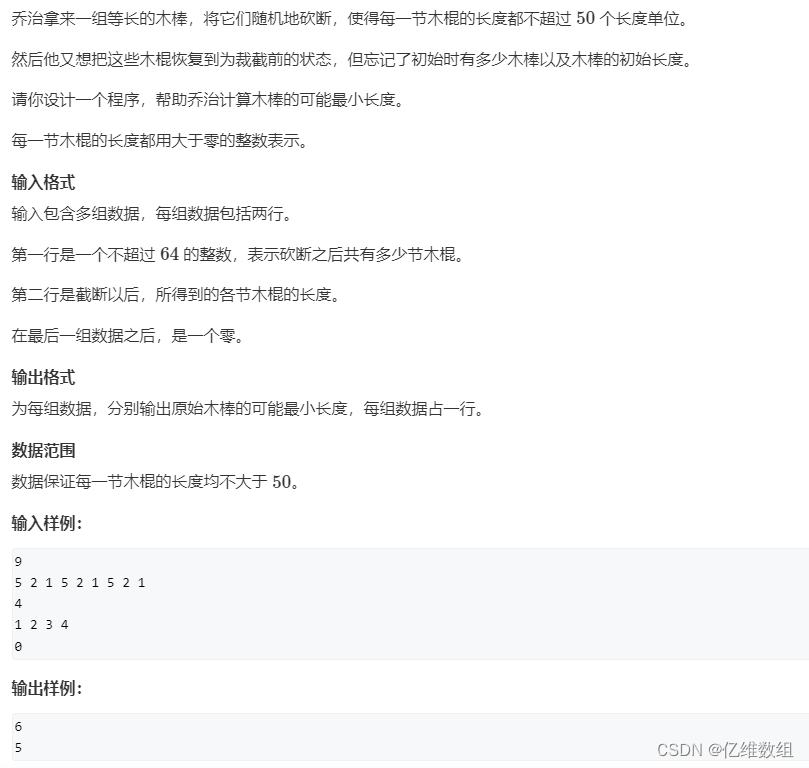
题目描述

 统一说明

本题思路来源于acwing算法提高课

木棍指题目输入数据所指的东西

木棒指最后由木棍拼接而成的最长的东西

看本文需要准备的知识

1.dfs基本思想

2.对“剪枝”这个词汇有一个基本的认识即可

整体分析

这个题目最终是求木棒的最短长度，所以我们可以从长度为1开始，每次加一，一直往后搜索，当搜索到解时，必然是最短长度。而在搜索的过程当中，显然长度满足：sum%length==0，这也是本题的一个小优化，dfs参数说明：

dfs(u,cur,start)

u：当前已经拼接好几根木棒

cur：当前正在拼接的这跟木棒已经拼好的长度

start：对同一根木棒，从哪一根木棍开始遍历

剪枝优化

A.优化搜索顺序

1.为了优先搜索分支较少的节点，我们可以让木棍按长度由大到小排序，优先搜索长度最长的木棍

B.排序等效冗余

1.按照组合数方式枚举，就是给每个木棍编号，有序的遍历，防止出现同一个木棒中由“1,2,3”拼成和“3,2,1”拼成的两种分支情况，毕竟一个木棒是如何拼成的跟木棍的顺序无关，所以对于同一根木棒拼接的时候，可以设置一个下标start，每次遍历木棍的时候从start开始遍历，即dfs(u,cur+w[i],start+1)

2.如果当前木棍加到某个木棒上之后失败了，那么跟这个木棍相同长度的木棍加到这个位置的时候也会失败

C.可行性剪枝

1.如果一个木棍放在某一个木棒的第一个位置时失败了，那么就没有遍历剩下的木棍放在这个位置的必要了，也就是说这时候我们需要回溯了，什么意思呢，我用递归树的方式带领大家理解：

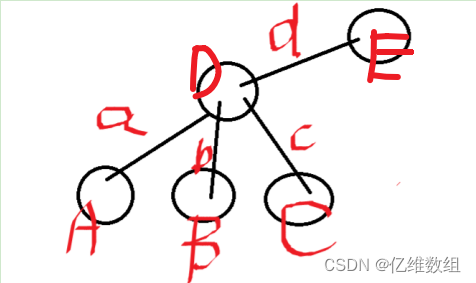
比如说A是在木棒x+1的第一个位置上放置木棍1，如果A的子树向A传递了false，那么接下来的路径就不是：“从A通过a回溯到D再通过b进入B”而是“直接通过a回溯到D再通过d回溯到E了”，其中B是在木棒x+1的第一个位置上放置木棍2，C同理，D是在木棒x的最后一个位置上放置某一个木棍

如何证明上述的剪枝的正确性呢？反证法

假设在木棒x的第一个位置上放木棍1失败，但往后继续搜索还能发现最终的正确方案，那么这个木棍1，一定会被放置在后续木棒的某个位置上，假设这个木棒是p，这个位置是n，这时候，我们可以把木棒p上的第一个位置的木棍和n位置上的木棍1交换，然后再把木棒x和木棒p做一个位置交换，发现：此时木棒x的第一个位置上放的是木棍1！！！与假设矛盾，证毕

2.如果一个木棍1放在一个木棒x的最后一个位置，并且可以使这个木棒的最长度达到length，但是在这个状态节点的子树给这个节点返回了false，那么就可以直接向上面一样，在回溯到D之后直接回溯到E，而不是进入B！

证明：反证法

假设在满足上述情况下，还可以找到某一个或多个木棍的拼接使得木棒x拼成length，此时木棍1一定在下面的某一个木棒的某一个位置中，我直接把木棍1和x此时后面为length长度的一个或几个木棍的拼接对换，就会发现：木棍1放在木棒x的最后一个位置，并且可以使这个木棒的最长度达到length！！！与假设矛盾，证毕

想说的话

感觉这题确实有点抽象，特别是可行性剪枝的两个部分，所以我采用了从递归树的角度，从底层，分析了这个问题，如果有没有看懂的或者我错了的地方，拜托各路大佬在评论区指出，谢谢！

满分代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=70;
int w[N];
int sum,length;
bool st[N];
int n;

bool dfs(int u,int cur,int start)
{
    if(u*length==sum)return true;
    if(cur==length)return dfs(u+1,0,0);
    for(int i=start;i<n;i++)
    {
        if(st[i]||cur+w[i]>length)continue;
        st[i]=true;
        if(dfs(u,cur+w[i],start+1))return true;
        st[i]=false;
        
        if(!cur||w[i]+cur==length)return false;
        int j=i+1;
        while(j<n&&w[i]==w[j])j++;
        i=j-1;
    }
    return false;
}

int main()
{
    while(cin>>n,n)
    {
        memset(st,false,sizeof st);
        sum=0;
        for(int i=0;i<n;i++)cin>>w[i];
        for(int i=0;i<n;i++)sum+=w[i];
        sort(w,w+n);
        reverse(w,w+n);
        length=1;
        while(true)
        {
            if(sum%length==0&&dfs(0,0,0))
            {
                cout<<length<<endl;
                break;
            }
            length++;
        }
    }
    return 0;
}