基础知识

理解U-Net网络结构需要相关知识点。

和CNN的关系

U-Net也是CNN（Convolutional Neural Network，卷积神经网络）的一种，所以也会涉及CNN的原理。关于CNN的一些内容，在之前的一篇文章介绍过“深度学习|CNN卷积神经网络”，这边就简单再说一下CNN原理中的“卷积、池化、全连接”，因为这些在后面U-Net结构理解的时候会用到。

卷积：主要作用是提取特征，通过一个过滤器/卷积核来过滤图像各个小区域，从而得到各个小区域的特征。

池化：提取某个区域的总结特征，主要作用是下采样(Downsampling)，能够数据降维，但是不会损坏识别结果。

全连接：主要作用是分类。通过卷积层和池化层的出来的特征，需要让全连接层对前面总结好的特征做分类判断。

不过U-Net网络，全是卷积和池化层，没有全连接层。

反卷积

卷积后，通常有3种结果：

1. valid卷积：结果图比原图小。
2. same卷积：结果图和原图一样大。
3. full卷积：结果图比原图大。

而其中的full卷积，就是反卷积又叫做上采样。关于以上三种卷积是如何形成，主要是源于在做卷积的时候，原图进行扩大的程度。

valid卷积：结果图比原图小。卷积的时候不对原图进行扩展或者扩展比较小。

same卷积：结果图和原图一样大。卷积的时候扩展一下原图，例如上面3×3的卷积，不做扩展导致每次边缘的像素点都没成为过卷积的中心像素，只需要对原图扩展一下就能包含边缘像素，从而实现same卷积。这种扩展操作，通常叫做padding。

full卷积：结果图比原图大。卷积的时候把原图比same卷积更大比例补0扩展。

ReLU激活函数

激活函数：神经网络中，每个节点代表一种特定输出函数，负责将神经元的输入映射到输出端。通常称为激活函数。

为什么要引入非线性激活函数：激活函数全用线性的，那样无论神经网络有多少层，输出都是输入线性组合，和没有隐藏层的效果差不多了。引入非线性函数作为激活函数，这样深层神经网络才有了意义，不再是输入的线性组合，而是可以逼近任意函数，更好拟合复杂的数据。另外，神经网络本身就是模拟生物神经元，生物神经元的行为本来就是非线性的。

ReLU函数的表达式：
$$f(x)=max(0,x)$$
从表达式看ReLU函数实际就是把大于0的数保留，小于0的数直接清零。

为什么使用ReLU激活函数：

• ReLU没有复杂的运算，计算简单高效，收敛速度也快。 Sigmoid等函数，算激活函数和反向传播求误差梯度时，涉及到指数、求导、除法等运算，计算量大。
• ReLU函数没有饱和区，不存在梯度消失问题。Sigmoid接近包和区时候，变换太慢，导数趋于0，而产生信梯度消失的情况，导致无法完成深层网络训练。
• ReLU使得一部分神经元输出为0，造成了网络的稀疏性，减少了参数之间相互依赖关系，一定程度上缓解了过拟合问题。

ReLU缺点：学习率过大的时候，可能造成大部分神经元清零。

补充：经典的Sigmoid函数，其表达式为$\sigma (x)=1/(1+e^{-x})$，能够把值映射到0~1。

U-Net入门

U-Net网络结构图

从上面的网络结构图来看，就知道为什么是U-Net了，网络结构就是一个U型。经典的编码器解码器结构，左边部分是编码器，右边部分是解码器。左边部分又被称为收缩路径，右边又被称为扩展路径，中间同一个曾灰色的箭头线被称为跳跃连接（Skip Connection）。

图中不同颜色箭头的解释：

1. 蓝紫箭头：3×3卷积核做卷积，再用ReLU激活函数输出特征通道。
2. 灰色箭头：进行裁剪和复制。
3. 红色箭头：2×2池化核进行最大池化/下采样。
4. 绿色箭头：2×2卷积核做反卷积/上采样
5. 青蓝箭头：1×1卷积核做卷积。

对上图结构部分做详细解释，其它部分可以自己参考详细解释来理解：

• 最左上角处理：输入图片大小为572×572，经过64个3×3的卷积核进行卷积，再通过ReLU函数后得到64个570×570的特征通道。把这570×570×64的结果再经过64个3×3的卷积核进行卷积，同样通过ReLU函数后得到64个568×568的特征提取结果。这就是第一层的处理，然后通过2×2的池化核，对图片下采样为原来大小的一半284×284×64。把284×284×64的结果，经过128个3×3×64的卷积核进行卷积，得到282×282×128（这部分实际上是对284×284×64全部做128个卷积）。
  
• 最右上角处理：392×392×128白蓝框来源于两个部分，蓝色部分是下面一层上采样/反卷积，196×196×128通过64个2×2卷积核反卷积，得到392×392×64；白色部分是同一层复制裁剪得到的，左边568×568×64结果复制再裁剪，得到392×392×64。蓝紫色箭头的过程不再多做解释，和“最左上角处理”介绍的是一样的。最右边最后一个青蓝箭头变换，388×388×64通过2个1×1的卷积核，得到388×388×2。

为什么需要跳跃连接

1. 反卷积只能扩大图片，不能还原图片，为了减少数据丢失，通过跳跃连接把同一层下采样的图片裁剪相同大小后增加特征层。大小不一致需要裁剪，主要是因为每次卷积都会丢失边界像素。
2. 结合深层信息和浅层信息，深层信息就是经过多次下采样后的低分辨率信息，能够提供分割目标在整个图片像素中上下文语义西悉尼，可以理解为特征，有助于物体的分类；浅层信息，通过跳跃连接从编码器传递到解码器上的高分辨率信息，能够给分割提供更加精细的特征。

U-Net的输入

由于不断valid卷积，边缘信息不够，卷积后图片越来越小，最终得到输出是会比输入要小的。为了保证操作后结果和原图大小一致，在输入前都会图片进行镜像扩展操作。

另外原作还用了Overlap-tile策略。医学图像通常都很大，不可能把原图输入网络，所以会进行切片，为了图片拼接部分分割更准确，采用了Overlap-tile策略，就是切片之间会有重叠。

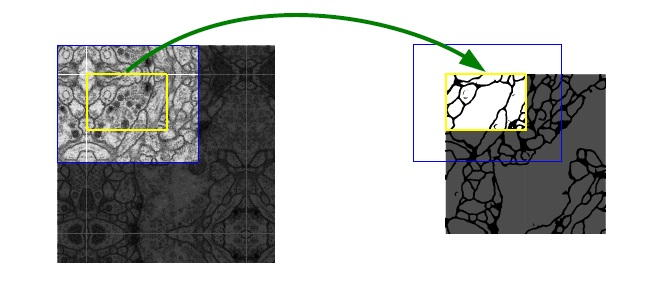
上面这张原图就做了镜像扩充，做了切片裁剪，输入蓝色部分图片通过U-Net最后能得到黄色有效区域处理结果。而Overlap-tile的切片重叠，应该指的是蓝色框会重叠。

U-Net的应用

主要解决的是医学领域的图像分割问题，目前基模型及其变种广泛应用于医学生物图像分割。

为什么适用于医学图像分割：

• 医学图像由于涉及病人隐私以及难获取等问题，数据相对较少，U-Net使用了丰富数据增强策略来扩充数据集，例如随机旋转、翻转、缩放等，可以提高模型的泛化能力和鲁棒性。
• U-Net模型是轻量级网络，参数量少，不容易过拟合，训练速度快。
• U-Net支持多通道多模态的医学图像输入，能够充分利用不同模态之间信息。多模态，例如MRI图像可能包含T1、T2、FLAIR等通道。
• 医学图像本身语义的信息就比较简单，结构比较谷顶。医学图像的信息密度远远不及平时拍的照片，应用场景也比较针对性，要做眼底就用眼底OCT，要做脑就用脑CT和脑MRI，都是针对固定的器官成像。所以高级语义信息和低级特征都显得很重要，U-Net的跳跃连接就排上用场了，就是结构图中灰色的箭头，结合低分辨率（提供物体类别标识的依据）和高分辨率信息（提供精确分割定位依据）。