多线程---线程安全问题及解决

news2025/2/23 7:04:19

文章目录

一个线程不安全的案例
造成线程不安全的原因
- 抢占式执行
- 多个线程修改同一个变量
- 修改操作不是原子的
- 内存可见性问题
- 指令重排序问题
如何让线程变得安全？
- 加锁
- volatile

一个线程不安全的案例

题目：有较短时间让变量count从0加到10_0000

解决方案：我们创建两个线程分别让count加5_0000次

结果：count < 10_0000


class Count{
    public int count = 0;
    
    public void increase(){
       count++;
    }

}
public class Demo {
    //验证线程不安全问题
    public static void main(String[] args) {
        Count count1 = new Count();


        // 操作同一个变量
        Thread thread1 = new Thread(() -> {
            for (int i = 0; i < 50000; i++){
                count1.increase();
            }
        });
        Thread thread2 = new Thread(() -> {
            for (int i = 0; i < 50000; i++){
                count1.increase();
            }
        });

        thread1.start();
        thread2.start();

        try {
            thread1.join();
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
        try {
            thread2.join();
        } catch (InterruptedException e) {
            e.printStackTrace();
        }

        System.out.println(count1.count);   //  <100000
    }
}

造成线程不安全的原因

抢占式执行

操作系统调度线程的时候，是一个“随机”的过程，当两个线程都参与调度的时候，谁先谁后不确定。

多个线程修改同一个变量

线程之间是“并发执行的”，当多个线程修改同一个变量时，多个线程同时获取到了变量值。某一个线程修改了变量，修改的结果不能被其他线程知道，其他线程还会修改原先获取到的值，导致结果错误。

如果修改的是不同的变量，线程之间独立执行，不会出现问题。

修改操作不是原子的

count++操作底层是三条指令在CPU上完成的：

load：把内存中的值读到CPU寄存器中；
add：count+1；
save：把寄存器的值写回内存

由于这三条指令不是原子的，两个线程在执行时就会有不同的执行顺序：
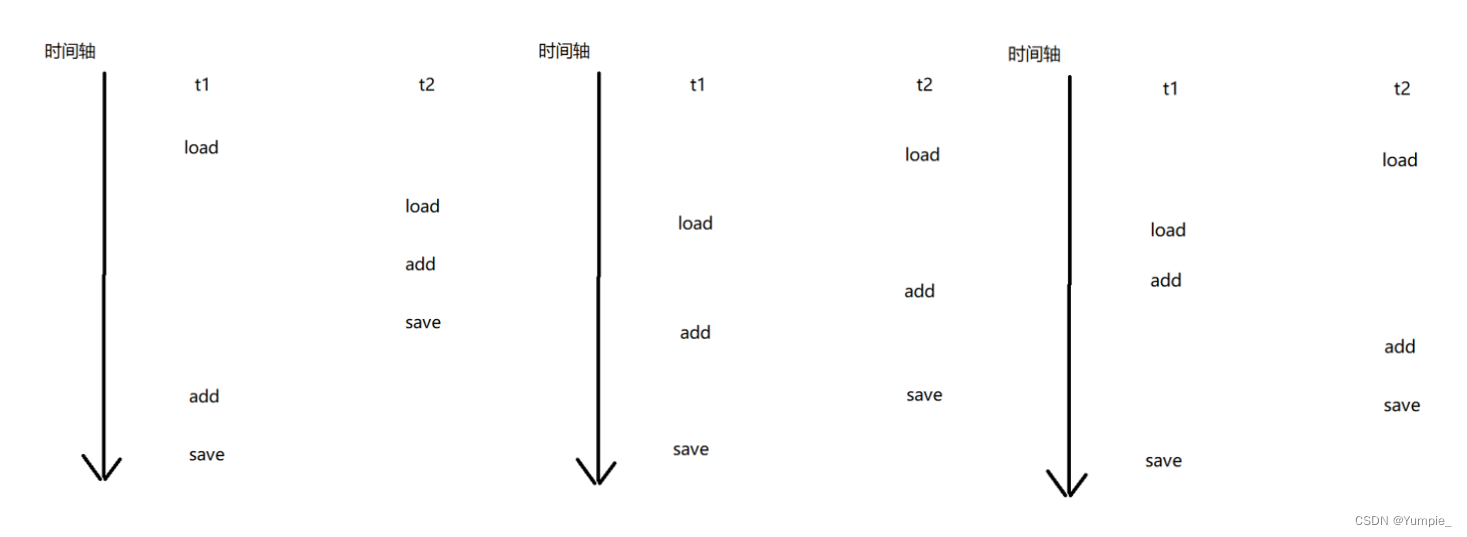
在这里插入图片描述
在这些执行顺序下，都会使count没有正确的++，使最终结果出错。

内存可见性问题

JVM优化引入的BUG。例如，两个线程在操作同一个变量，一个线程读并且比较，一个线程修改。假设读操作非常频繁的情况下，比较操作也会非常的频繁。但是读是从内存中读，比较是在CPU里比较。比较的速度远远大于读的速度。而且每次读到的值还一样，这时编译器就会大胆优化：只读取一次，后面就不从内存中读了。每次比较都和前面读取到的值比较，不和内存中的值比较。这时另一个线程把内存中的值修改了但是这个线程比较的还时原来的值，就会有问题。