Hello,今天事10月27日,距离刚开始写博客已经过去挺久了,我也不知道是什么让我坚持这么久,但是学校的课真的很多,很少有时间多出来再学习,有些科目马上要考试了,我还不知道我呢不能过哈哈哈,今天的内容主要是想和大家继续分享之间的时间复杂度和空间复杂度,再拿出几个oj题目,我们一个一个来分析,那开始我们今天的学习吧。
那我们先来给大家补充几个时间复杂度的题目。
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1) * N;
}
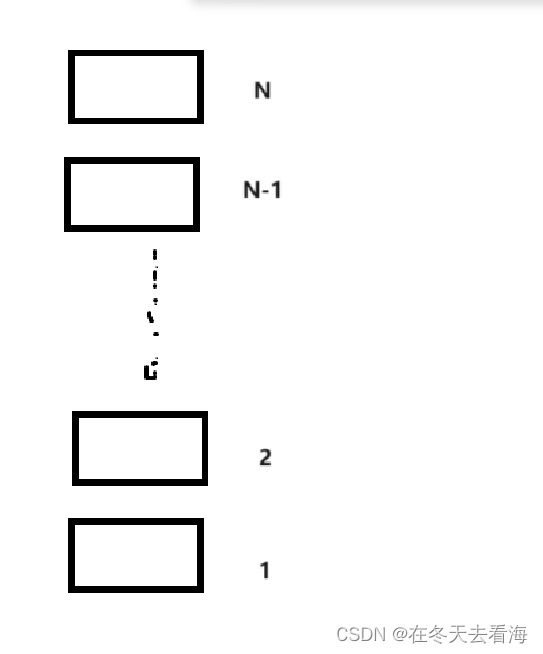
时间复杂度不是来算时间的,我们最后还是算的次数,这里N的阶乘就是要知道N-1的大小,我们要知道N-1的值的话,就得先知道N-2的值,依次这样类推下去,一直到1的时候,我们递归才开始调用返回,那我们一直到1的话就是需要N次,所以时间复杂度就是N次
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
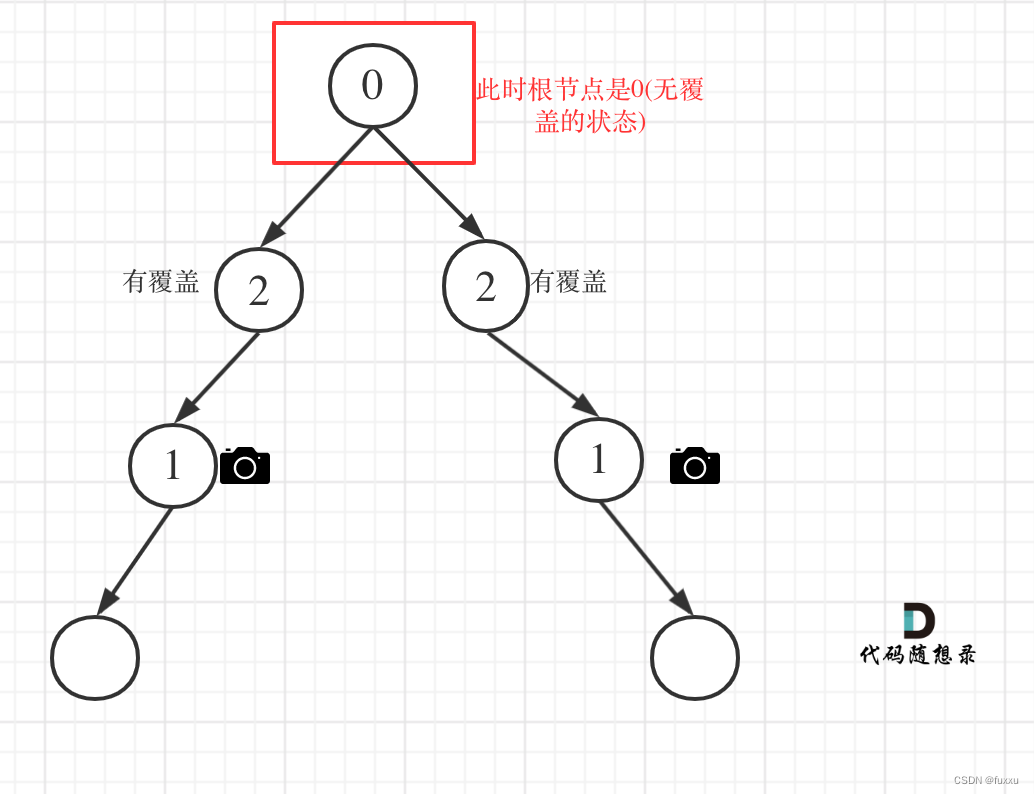
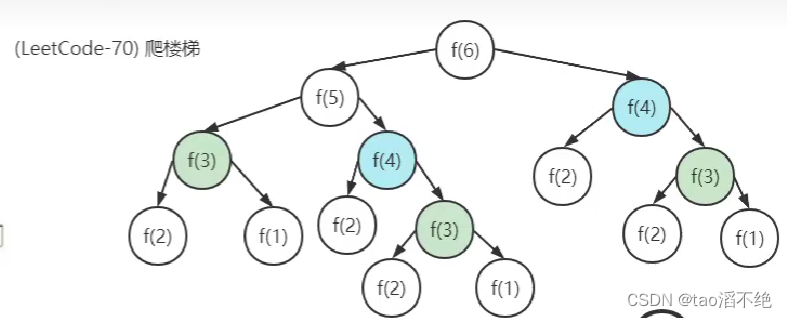
这个题目有点难懂,它的结构就是相当于一个二叉树,但是不完整的二叉树,我们这里也是递归往下走的,如果我们要求N的斐波那契,就必须得先知道N-1和N-2的斐波那契数,依次类推,要想知道N-1的斐波那契就必须先知道N-2和N-3的斐波那契数,一直到1和2递归才开始往回走,那我们还是来画图来解决。
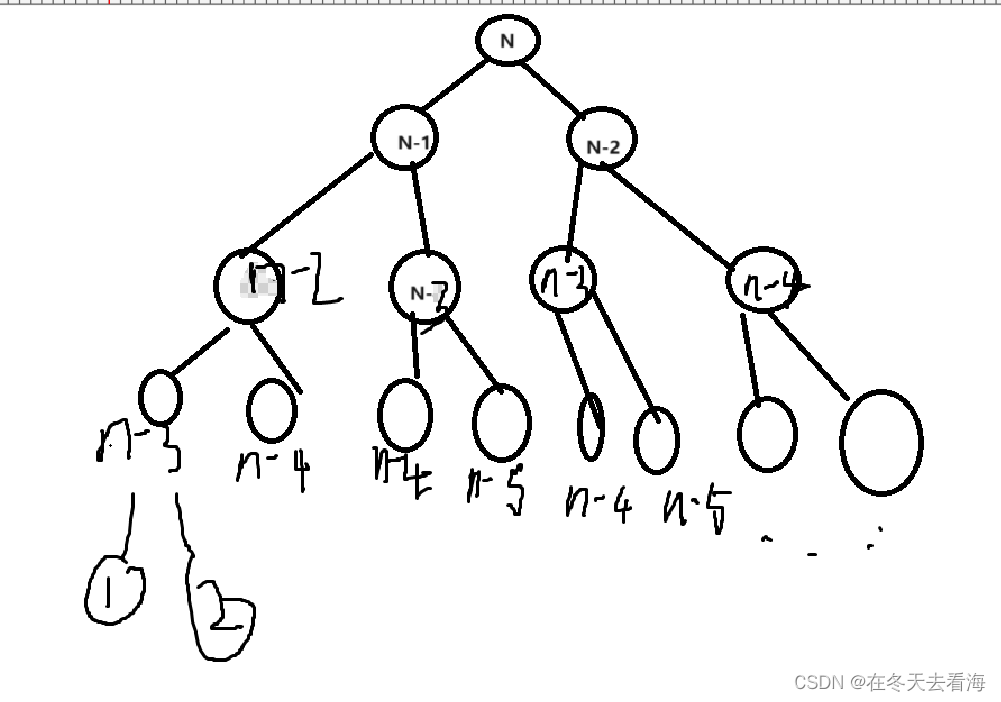
属实画的太抽象了,就是我们一直往下递归,一直到1和2才开始结束,但是我们之前说过其实这个不是一个完整的递归二叉树,原因是有些提前结束了,但是因为时间复杂度是可以通过估算的,我们看第一层有1个,第二层有2个依次往下就是一个等比数列,每个都是×2,那就是等比数列求和,大家肯定会,用大O渐进表示法就是O(2的n次方)
空间复杂度
空间复杂度就是开的空间,我们这个程序需要多大的空间,官方一点的回答请看下面。
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
我们直接上题目来讲解,一个男人强不强,肯定得是看他实战(狗头)
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
我们这个开辟了多少空间,这里我们开辟很多变量,但是这些变量也都是常数次的,因此时间复杂度就是O(1),其他也没消耗和额外的开辟空间,我们都知道我们再调用函数的时候,是会创建函数栈帧的,只会在这个函数栈帧中压栈和出栈,但是我们这个操作都是常数次,
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
这个其实很明显,我们malloc就是开空间,开N个那空间复杂度就是O(N),这里都不用多想。
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
这里我们递归下去,就是会一直开辟函数栈帧,一直到N==0的时候他们才开始返回,所以这里空间复杂度其实就是O(N),这里给大家在同样的发出一个其他的问题,也是斐波那契函数。
来加个餐
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
我们来看看这个的空间复杂度,这里其实我们要牢记一句话,就是时间是不能累积的,空间是可以累积的,那我们求第N个斐波那契的时候,有很多空间其实是相同的,所以这里就会有重复利用空间的情况,但是虽然看起来好像是开辟了2的n次方的空间,但是他们好多重复了,其实就是只有O(N)的空间复杂度。
我们可以来看一下空间可以重复利用,但是时间不能进行重复利用的例子。
void Fun1()
{
int a = 0;
printf("%p\n", &a);
}
void Fun2()
{
int a = 0;
printf("%p\n", &a);
}
int main()
{
Fun1();
Fun2();
return 0;
}
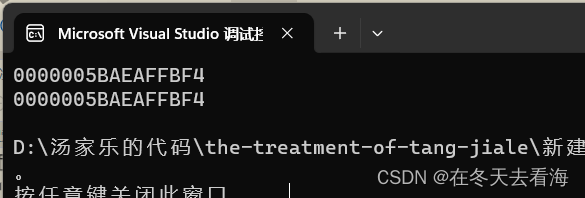
我们来看看他们的地址是相同的。
这个就是Fun1函数和Fun2函数的利用的空间其实是同一个空间。
![[SQL开发笔记]UPDATE 语句:更新表中的记录](https://img-blog.csdnimg.cn/ba6f4824fbc5486c91701db622da136c.png)