一、朴素筛法——埃氏筛法

1、问题描述

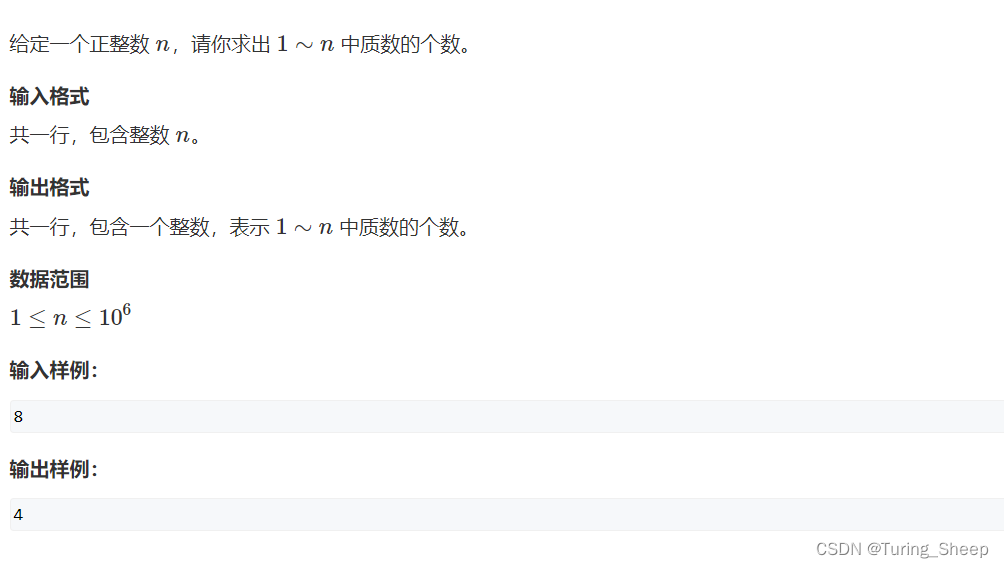
2、算法思路

我们从2开始枚举，因为2一定是质数，那么2的倍数就一定不是质数。
这个是很好理解的，因为2的倍数一定是会被2整除，所以2的倍数就一定不是质数。因此我们可以直接删除掉2的倍数。
那么接着枚举，3是质数，所以3的倍数也一定不是质数。同理我们删掉所有是3的倍数的数。

按照上述的思路，如果我们某个$i$没有被删掉的话，$i$一定是质数。为什么？

因为$i$没有被删掉说明$i$不是$2$到$i-1$的倍数，也就是说$2$到$i-1$不存在$i$的因数。所以$i$必定是质数。

3、代码实现

#include <iostream>
#include <algorithm>
using namespace std;
const int N= 1000010;
int primes[N], cnt;//记录所有的质数
bool st[N];//看是否被删掉
void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}
int main()
{
    int n;
    cin >> n;
    get_primes(n);
    cout << cnt << endl;
    return 0;
}

埃氏筛法的时间复杂度是$O(nlog(logn))$，可以近似看作$O(n)$

二、线性筛法——欧拉筛

1、朴素筛法的弊端

对于刚刚的朴素筛法而言，可能会存在重复删除一个合数的情况。

比如，$6$是一个合数，那么当$i=2$的时候，6是2的倍数，6会被删除一次。当$i=3$的时候，6也是3的倍数，所以6又会被删除一次。所以导致埃氏筛法的时间复杂度中有一个$loglogn$的系数。

而下面介绍的欧拉筛就解决了重复删除的问题，从而去掉了这个系数，使得时间复杂度变成了真正的$O(n)$。所以欧拉筛也被成为线性筛。

2、欧拉筛

（1）算法思路

我们还以刚刚的6为例子，按照算数基本定理，6可以写成$2\ast 3$两个质数相乘的形式。

为了避免重复，我们只删除具有相同最小质因数的数。

刚刚的埃氏筛法是去枚举质数$i$，然后在循环每个倍数$j$，然后删除质数和倍数相乘组成的合数$i\ast j$。如果还是刚刚的循环的话，我们无法保证我们枚举的那个质数$i$就是最小的质因数，为什么呢？

因为随着$j$的增加，我们内部循环的倍数$j$很有可能被一个比$i$小的质数$m$整除，此时合数$i\ast j$的最小质因数就不是$i$，而是$m$。

而当$j$继续变化，$i\ast j$的最小质因数可能又变成了另一个数。所以此时$i\ast j$的最小质因数是摇摆不定的。

所以还按照刚刚埃氏筛法的循环设计去枚举的话，是很难优化成欧拉筛的思路的。

所以，我们需要重新设计一下循环：

刚刚的朴素筛主要问题在于内循环是倍数，这个倍数是不可控的。因此，我们颠倒一下顺序（此时的答案一定是不会漏解的），先去枚举倍数，然后再去从小到大枚举质数（把这个质数当作最小的质因数）来循环。

这个倍数就是$2$到$n$的所有数字来充当的，因为我们要保证倍数和质数的乘积小于等于$n$。所以我们的倍数是不会超过$n$的，因此我们让这个范围的数字来充当倍数是没有问题的。

这样做有什么好处呢？

这样做就能保证我们二者相乘得到的$i\ast j$的最小质因数是一个递增的状态，是可控的。

但是我们注意的是，我们的$i$ % $j！=0$，为什么呢？当前$i\ast j$最小的质因数是$j$，没错，为了方便我们标记此时的$j$为$j_1$。那么接下来，我们会枚举比$j_1$大的质数$j_2$，目的是把$j_2$当成最小的质因数，但是$i\ast j$中的$i$的质因数已经包括了$j_1$，所以$i\ast j_2$的最小质因数也是$j_1$，不是$j_2$。也就是说我们再去枚举$>j_1$的质数已经没有意义了。

我们第二层循环的目的就是去逐步枚举越来越大的质数当作最小质因数，但是$j_1$存在时，后面的所有$i\ast j_n$组成的合数的最小质因数都是$j_1$。也就是说，后续的枚举没有意义了，因此当出现$j_1$的时候，我们就可以终止循环了。

如果不终止的话，就会出现朴素算法的重复删除，因为我们利用质因数$j_2$删除了最小质因数为$j_1$的数字，而这些数字在枚举$j_1$的时候就被删掉了。

就相当于我们刚刚举得例子，6=2*3，用2已经删掉了6，但是我们又利用3去删除了一次。

很多人还会有一个担心，因为我们外层枚举的是倍数，会不会说因为删除了某个数，而让以这个数为倍数的质数漏掉了呢？

答案是不会的，因为这个数既然删掉了，那么它就是合数，合数充当倍数组成的数也一定是合数，所以不会漏解。

所以，我们如果不加跳出循环的判断语句，这个算法就会变成埃氏算法。

（2）代码实现

#include <iostream>
#include <algorithm>
using namespace std;
const int N= 1000010;
int primes[N], cnt;
bool st[N];
void get_primes(int n)
{
    for(int i=2;i<=n;i++)
    {
    	//如果没被删掉，就是质数
        if(!st[i])primes[cnt++]=i;
        
        for(int j=0;primes[j]<=n/i;j++)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)break;
        }
    }
}

int main()
{
    int n;
    cin >> n;
    get_primes(n);
    cout << cnt << endl;
    return 0;
}