1739. 放置盒子

题目：

有一个立方体房间，其长度、宽度和高度都等于 n 个单位。请你在房间里放置 n 个盒子，每个盒子都是一个单位边长的立方体。放置规则如下：

你可以把盒子放在地板上的任何地方。
如果盒子 x 需要放置在盒子 y 的顶部，那么盒子 y 竖直的四个侧面都 必须 与另一个盒子或墙相邻。
给你一个整数 n ，返回接触地面的盒子的 最少 可能数量。

---

示例 1

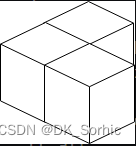
输入：n = 3
输出：3
解释：上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角，对应左侧位置。

---

示例 2：

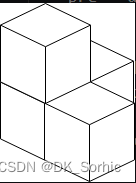
 输入：n = 4
输出：3
解释：上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角，对应左侧位置。

---

示例 3：

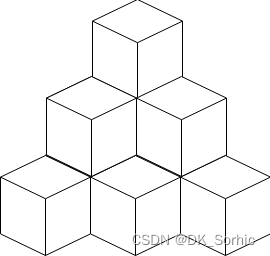
 输入：n = 10
输出：6
解释：上图是 10 个盒子的摆放位置。
这些盒子放在房间的一角，对应后方位置。

---

提示：

1 <= n <= 109

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/building-boxes
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

---

思路：

先看看n可以堆放几层满的，所谓满的是指不能再在积木上任何地方堆积而不增加底部的投影面积，因此只能从底部开始堆起。
最底层若新加k个积木，则总的来说可以增加k + (k - 1) + ... + 1 个积木而不增加投影面积。
因此模拟这个过程即可

---

代码：

class Solution {
public:
    int minimumBoxes(int n) {
    	int shadow = 0;

		// 积木可以堆几层（都是满堆）
    	int floor = 1;
    	while (n > (1 + floor) * floor >> 1) {
    		shadow += floor;
    		n -= (1 + floor) * floor >> 1;
    		floor ++;
    	}

		// 对多余的积木的处理
        int i = 1;
        while ((1 + i) * i >> 1 < n) i++;
    	shadow += i;

    	return shadow;
    }
};