题目链接
Leetcode.1465 切割后面积最大的蛋糕
rating : 1445
题目描述
矩形蛋糕的高度为 h h h 且宽度为 w w w,给你两个整数数组 h o r i z o n t a l C u t s horizontalCuts horizontalCuts 和 v e r t i c a l C u t s verticalCuts verticalCuts,其中:
- h o r i z o n t a l C u t s [ i ] horizontalCuts[i] horizontalCuts[i] 是从矩形蛋糕顶部到第 i i i 个水平切口的距离
- v e r t i c a l C u t s [ j ] verticalCuts[j] verticalCuts[j] 是从矩形蛋糕的左侧到第 j j j 个竖直切口的距离
请你按数组 h o r i z o n t a l C u t s horizontalCuts horizontalCuts 和 v e r t i c a l C u t s verticalCuts verticalCuts 中提供的水平和竖直位置切割后,请你找出 面积最大 的那份蛋糕,并返回其 面积 。由于答案可能是一个很大的数字,因此需要将结果 对 1 0 9 + 7 10^9 + 7 109+7 取余 后返回。
示例 1:

输入:h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出:4
解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色的那份蛋糕面积最大。
示例 2:
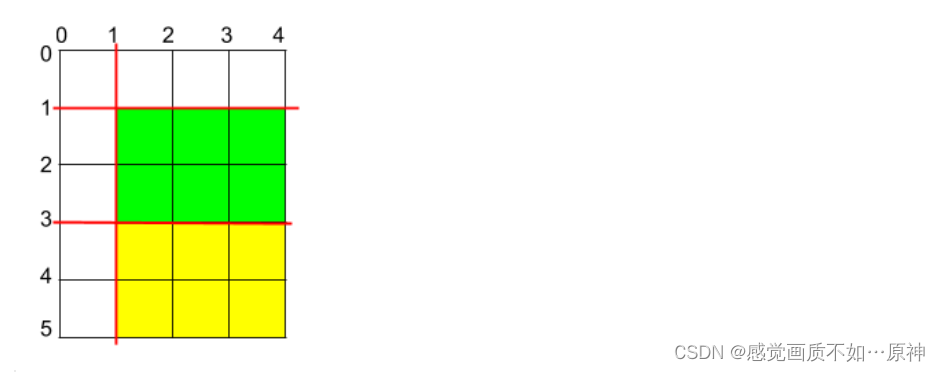
输入:h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出:6
解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色和黄色的两份蛋糕面积最大。
示例 3:
输入:h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出:9
提示:
- 2 ≤ h , w ≤ 1 0 9 2 \leq h, w \leq 10^9 2≤h,w≤109
- 1 ≤ h o r i z o n t a l C u t s . l e n g t h ≤ m i n ( h − 1 , 1 0 5 ) 1 \leq horizontalCuts.length \leq min(h - 1, 10^5) 1≤horizontalCuts.length≤min(h−1,105)
- 1 ≤ v e r t i c a l C u t s . l e n g t h ≤ m i n ( w − 1 , 1 0 5 ) 1 \leq verticalCuts.length \leq min(w - 1, 10^5) 1≤verticalCuts.length≤min(w−1,105)
- 1 ≤ h o r i z o n t a l C u t s [ i ] < h 1 \leq horizontalCuts[i] < h 1≤horizontalCuts[i]<h
- 1 ≤ v e r t i c a l C u t s [ i ] < w 1 \leq verticalCuts[i] < w 1≤verticalCuts[i]<w
- 题目数据保证 h o r i z o n t a l C u t s horizontalCuts horizontalCuts 中的所有元素各不相同
- 题目数据保证 v e r t i c a l C u t s verticalCuts verticalCuts 中的所有元素各不相同
解法:排序 + 贪心
蛋糕的面积为
a
r
e
a
=
(
h
o
r
i
z
o
n
t
a
l
C
u
t
s
[
i
]
−
h
o
r
i
z
o
n
t
a
l
C
u
t
s
[
i
−
1
]
)
×
(
v
e
r
t
i
c
a
l
C
u
t
s
[
i
]
−
v
e
r
t
i
c
a
l
C
u
t
s
[
i
−
1
]
)
area = (horizontalCuts[i] - horizontalCuts[i - 1]) \times (verticalCuts[i] - verticalCuts[i-1])
area=(horizontalCuts[i]−horizontalCuts[i−1])×(verticalCuts[i]−verticalCuts[i−1])
用于相乘的这两项是独立的,所以我们可以先分别找到各自最大的一项,即 m a x ( h o r i z o n t a l C u t s [ i ] − h o r i z o n t a l C u t s [ i − 1 ] ) max(horizontalCuts[i] - horizontalCuts[i - 1]) max(horizontalCuts[i]−horizontalCuts[i−1]) 和 m a x ( v e r t i c a l C u t s [ i ] − v e r t i c a l C u t s [ i − 1 ] ) max(verticalCuts[i] - verticalCuts[i-1]) max(verticalCuts[i]−verticalCuts[i−1])。
再相乘就得到最终的答案了。
时间复杂度: O ( n × l o g n ) O(n \times logn) O(n×logn)
C++代码:
const int MOD = 1e9 + 7;
class Solution {
public:
int get_max_size(vector<int>& cuts , int size){
sort(cuts.begin(),cuts.end());
int ans = max(cuts[0] , size - cuts.back());
int n = cuts.size();
for(int i = 1;i < n;i++){
ans = max(ans , cuts[i] - cuts[i - 1]);
}
return ans;
}
int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
int max_h = get_max_size(horizontalCuts,h);
int max_w = get_max_size(verticalCuts,w);
return max_h * 1LL * max_w % MOD;
}
};