观察数据生成器可以发现对于每次操作均有 。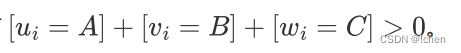

考虑将这些三元组想象成空间直角坐标系中 为对顶点的长方体。 将操作分成两部分，一部分是对 轴同时操作的，可以一开始就用前缀 统计完，将长方体变 成一个底面为阶梯状的直棱柱。另一部分是对 或 操作的，考虑从小到大枚举 ，然后将 的操作变成一条横线或一条竖线，容易发现这两条线也是具有单调性的，于是每层留下的点数可 以直接计算。 最后用总点数减去剩下的点数即为删除的三元组数量，由于答案最大可能到 ，所以需要使 用高精或 __int128 。总时间复杂度为

 实现代码如下：

#include <bits/stdc++.h>
using namespace std;

const int N = 3e7 + 10;
typedef unsigned long long ull;

int n, A, B, C, u[N], v[N], w[N];

ull Rand (ull &k1, ull &k2) {
    ull k3 = k1, k4 = k2;
    k1 = k4;
    k3 ^= (k3 << 23);
    k2 = k3 ^ k4 ^ (k3 >> 17) ^ (k4 >> 26);
    return k2 + k4;
}

void GetData () {
    ull x, y;
    cin >> n >> A >> B >> C >> x >> y;
    for (int i = 1; i <= n; i++) {
        u[i] = Rand(x, y) % A + 1;
        v[i] = Rand(x, y) % B + 1;
        w[i] = Rand(x, y) % C + 1;
        if (Rand(x, y) % 3 == 0) u[i] = A;
        if (Rand(x, y) % 3 == 0) v[i] = B;
        if ((u[i] != A) && (v[i] != B)) w[i] = C;
    }
}

void Write (__int128 x) {
    if (x < 10) cout << (int)x;
    else Write(x / 10), cout << (int)(x % 10);
}

int h[N], l[N], Mx[N], My[N];

int main () {

    GetData();

    for (int i = 1; i <= n; i++) {
        if (w[i] == C) h[u[i]] = max(h[u[i]], v[i]);
        else if (u[i] == A) My[w[i]] = max(My[w[i]], v[i]);
        else if (v[i] == B) Mx[w[i]] = max(Mx[w[i]], u[i]);
    }

    for (int i = A; i >= 1; i--) h[i] = max(h[i], h[i + 1]);
    for (int i = C; i >= 1; i--) Mx[i] = max(Mx[i], Mx[i + 1]);
    for (int i = C; i >= 1; i--) My[i] = max(My[i], My[i + 1]);

    for (int i = 1, now = A; i <= B; i++) {
        while (now && h[now] < i) now--;
        l[i] = now;
    }

    __int128 ans = 0, sum = 0, All;
    for (int i = 1, Lx = A, Ly = B; i <= C; i++) {
        while (Lx > Mx[i]) sum += B - Ly - max(0, h[Lx] - Ly), Lx--;
        while (Ly > My[i]) sum += A - Lx - max(0, l[Ly] - Lx), Ly--;
        ans += sum;
    }
    All = A, All *= B, All *= C;
    Write(All - ans);

    return 0;
}