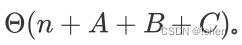有任何的书写错误、排版错误、概念错误等，希望大家包含指正。

由于这部分的参考资料比较少，网上大部分资料重复且不完整，对于一些关键计算没有推导，所以这里我主要讨论几篇论文和讲义。但是这些论文和讲义之间也有些许差别，讨论的过程中我会加入自己的理解，难免存在错误，欢迎大家讨论。

最大熵马尔可夫模型

最大熵马尔可夫模型（maximum-entropy Markov model，MEMM）又称为条件马尔可夫模型（conditional Markov model，CMM）。单纯顾名思义的话，可能会认为最大熵马尔可夫模型是最大熵模型与马尔可夫模型的融合，但其实，它结合了最大熵模型和隐马尔可夫模型（HMM）的共同特点，被广泛应用于序列标注问题。

模型介绍与对比

我们的讨论是以观测与状态是一对一关系为前提，而不考虑多个观测对应一个状态的情况，比如：Yellow River 被认为是一个专有名词，而不是一个形容词和一个名词。

先对比 MEMM 与 HMM。二者的概率图如下。

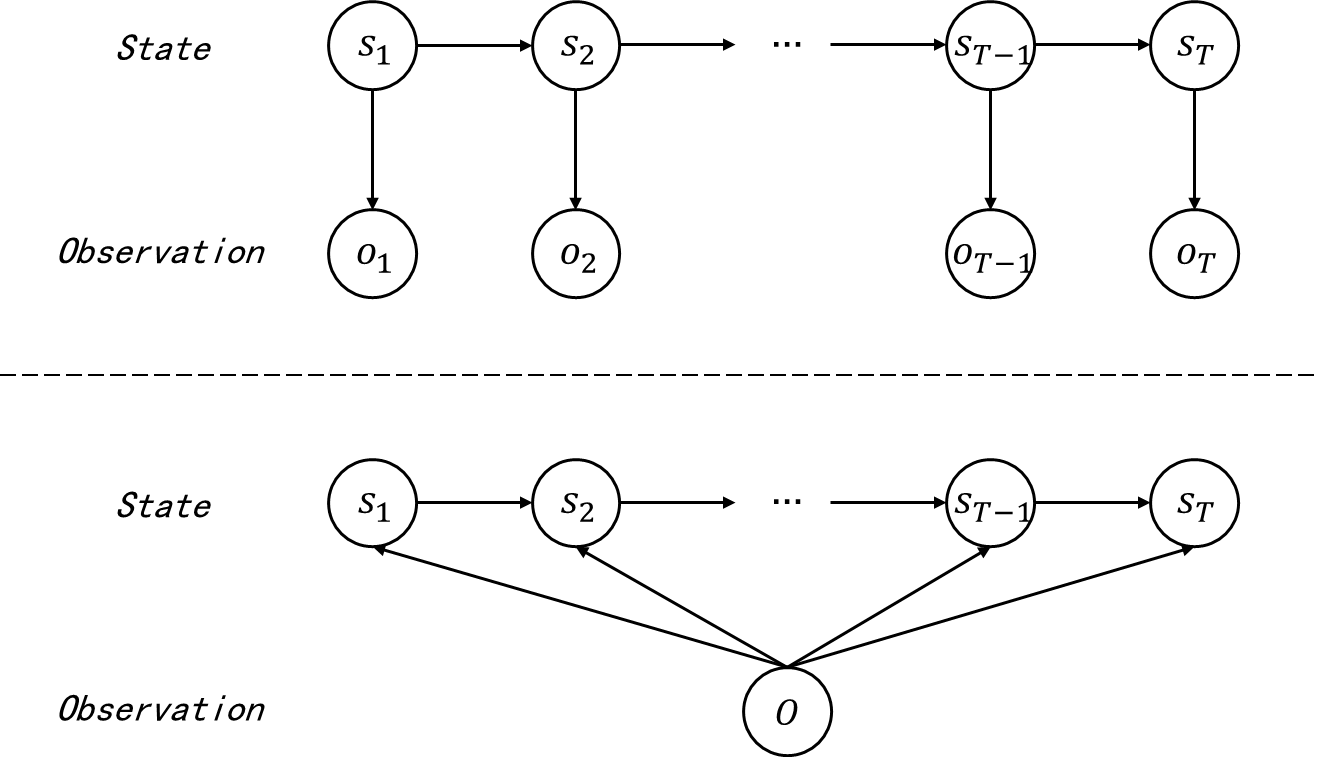
图 1    HMM (上)和满足一阶马尔可夫性质的 MEMM (下)

图 $1$ 中的中的 MEMM 概率图为满足一阶马尔可夫性质的 MEMM，二阶 MEMM 的概率图只需要在此基础上加上从 $s_{t-2}$ 到 $s_t$ 的箭头。

对比 HMM 和 MEMM 的概率图，HMM 认为观测作为输出值与当前时刻的状态有关，而 MEMM 认为当前时刻的状态由之前时刻的状态和全部观测（或者多个时刻的观测值）共同确定，也就是说，在 MEMM 中观测不再独立，甚至作为输入值用于确定每个时刻的状态。这种性质决定了 HMM 是生成式模型，而 MEMM 是判别式模型。生成式模型对概率图表示的联合概率进行建模，再利用联合概率计算后验概率进行解码等操作；判别模型直接对概率图表示的条件概率建模，避免了对联合概率建模，使得解码等操作更加直接。

根据 HMM 的概率图，我们知道 HMM 直接对联合概率 $P(S,O)$ 建模，即
$$P(S,O)=\prod _{t=1}^{T}P(s_t\mid s_{t-1})P(o_t\mid s_t)$$
为了公式简洁、形式统一，不再特殊考虑 $t=1$ 时的初始概率分布。

根据 MEMM 的概率图，我们对条件概率建模，有
$$P(S\mid O)=\prod _{t=1}^{T}P(s_t\mid s_{t-1},O)\text{\hspace{1em}(1)}$$

也有部分参考资料会进一步简化模型，将 HMM 概率图中状态到观测的箭头反向后的概率图作为 MEMM 的概率图，这相当于他们认为每个时刻的状态 $s_t$ 不是与整个观测序列 $O$ 有关，而是与当前时刻的观测值 $o_t$ 有关。这会影响模型效果，但不会影响我们的推导和理解。

另外，对于每个时刻的状态，MEMM 考虑的是观测序列和之前时刻的状态，而 HMM 仅考虑之前时刻的状态。在序列标注问题中，将文本上下文包含的信息（特征）作为解码输出状态的判断依据显然更加合理，所以 MEMM 考虑整个观测序列是必然选择。如果将整个观测序列视为输入，那么输入值很可能无法完整枚举，因此需要大量的特征来刻画观测序列。如在文本中识别一个未见的公司名字时，除了传统的单词识别方法以外，还需要用到很多特征信息，如大写字母、结尾词、词性、格式、在文本中的位置等信息。也就是说，我们无法直接使用大量不同的观测序列，故需要提取其中的上下文信息（特征）来代表输入的观测序列。HMM 不适合处理用很多特征描述观测序列的情况，因为 HMM 在建模时不会将整个观测序列视为输入值，也就无法提取充足的特征。为此，MEMM 直接采用条件概率模型，从而使观测序列可以用特征表示，借助最大熵框架进行特征选取。

注意，对于某个时刻状态的解码一般不以整个观测序列作为输入，而是选取该时刻周围若干时刻的观测作为输入。之所以上文以“整个观测序列”进行叙述，其一是为了强调 MEMM 相比于 HMM 更加注重整体、上下文，其二是因为如此叙述会使得语言更加简洁。

对比 MEMM 与最大熵模型。最大熵模型没有考虑时序关系，以观测序列为条件，每个词是单独进行判别的，状态之间的关系无法得到充分利用，但是最大熵模型的优点在于可以使用任意的复杂特征。具有时序关系的 HMM 可以建立状态之间的马尔可夫性，这是最大熵模型所没有的。一个很自然的想法就是将两者的优势结合起来，这就得到了最大熵马尔可夫模型。

最大熵模型是一种特殊的逻辑回归模型（softmax），所以在有些文章中会看到。

学习问题

文献 [1 McCallum et al. ，2000] 与文献 [3 Michael Collins 讲义] 有些许不同，这里分开讨论。

基本假设，可能的状态数为 $N$，所有可能的状态的集合为 Q = { q 1 , q 2 , … , q N } Q = \{q_1,q_2,\dots, q_N\} Q={q1​,q2​,…,qN​}。

先讨论文献 [3]。假设训练集中的样本个数为 $D$，样本的序列长度均为 $T$，第 $d$ 个样本的状态序列 $S_d=(s_1^{(d)},s_2^{(d)},\dots ,s_T^{(d)})$，观测序列为 $O_d=(o_1^{(d)},o_2^{(d)},\dots ,o_T^{(d)})$。对于第 $d$ 个样本的每个时刻 $t$，可以定义一个三元组
$$h_t^{(d)}=<{\mathcal{S}}_d,{\mathcal{O}}_d,t>$$
其中 ${\mathcal{S}}_d$ 为状态序列 $S_d$ 的子集，在文献 [3] 中，由于讨论的是二阶马尔可夫性的 MEMM，所以 S d = { s t − 2 ( d ) , s t − 1 ( d ) } \mathcal S_d = \{s^{(d)}_{t-2},s^{(d)}_{t-1}\} Sd​={st−2(d)​,st−1(d)​}；${\mathcal{O}}_d$ 为观测序列 $O_d$ 的子集，在文献 [3] 中 ${\mathcal{O}}_d=O_d$；$t$ 表示序列的位置。可见，$h_t$ 捕获 $s_t$ 的条件信息，可以将 $h_t$ 与 HMM 中的 $o_t$ 类比理解，只不过在 MEMM 中不再简单地以某个时刻的观测值作为条件，而是以一组信息作为条件。另外，因为本文为了统一，仅讨论一阶 MEMM，故 S d = { s t − 1 ( d ) } \mathcal S_d = \{s_{t-1}^{(d)}\} Sd​={st−1(d)​}；至于 ${\mathcal{O}}_d$ ，在理论推导中是取 $O_d$ 的真子集还是与之相同都无所谓。

这样一来，特征函数 $f$ 会将 $h$ 和 $s$ 一并考虑，即
$$f(h,s)=\{\begin{array}{ll}1,& \text{if}(h,s)\text{and}\text{meet}\text{certain}\text{conditions}\\ 0,& \text{otherwise}\end{array}$$
式 $(1)$ 可以被写为
$$P(S\mid O)=\prod _{t=1}^{T}P(s_t\mid h_t)\text{\hspace{1em}(2)}$$
根据最大熵模型，其中 $P(s_t\mid h_t)$ 可以表示为
$$P(s_t\mid h_t;w)=\frac{\exp \left(w\cdot f(h_t,s_t)\right)}{\sum _{i=1}^N\exp \left(w\cdot f(h_t,s=q_i)\right)}\text{\hspace{1em}(3)}$$
其中 $w$ 和 $f$ 均为向量，$w\cdot f$ 表示内积运算。

文献 [3] 中直接给出了采用正则化的对数似然函数来学习模型参数 $w$，
$$\begin{array}{rl}L(w)& =\log \prod _{d=1}^D\prod _{t=1}^{T}P(s_t^{(d)}\mid h_t^{(d)};w)-\frac{\lambda }{2}\Vert w{\Vert }_2^2\\ & =\sum _{d=1}^D\sum _{t=1}^T\log P(s_t^{(d)}\mid h_t^{(d)};w)-\frac{\lambda }{2}\sum _{i=1}^n{w}_i^2\end{array}\text{\hspace{1em}(4)}$$
将全部样本每个时刻的条件概率之积作为似然函数，同时引入正则化项。加入正则化项主要是考虑到最大似然估计可能会遇到特征函数数量特别大的情况，从而导致个别特征函数只有一个样本符合的极端情形。可以想象到，这些特征函数对应的权重会趋于无穷，所以样本对应的条件概率为 $1$，这使得模型对于这些样本不具有很好的泛化能力。举个简单的例子，训练集中满足特征函数 $f_1$ 的只有样本 Yellow River，训练后的特征函数 $f_1$ 对应的权重 $w_1$ 趋于无穷，$P(s_t=\mathrm{River}\mid s_{t-1}=\mathrm{Yellow})=1$，也就是说，训练后的模型只要遇到 Yellow 就一定会将下一个时刻的状态解码为 River，这显然是不合理的，加上正则化项以缓解这类问题。

我认为文献 [3] 中的学习算法，即式 $(4)$ 有些许不合理，因为无法类似于最大熵模型一样证明对偶函数与对数似然函数等价。

---

再来讨论我认为比较合理的文献 [1] 提出的学习方案。

该文献提出的方案为，在一阶 MEMM 的前提下，将 $<s_{t-1}^{(d)},s_t^{(d)},O_d>$ 视为一个单元，那么对于大小为 $D$，各序列长度均为 $T$ 的训练集而言，可以拆分出大约 $D\times T$ 个单元。这些单元相当于特征为 $h_t^{(d)}=<s_{t-1}^{(d)},O_d,t>$，标签为 $s_t^{(d)}$ 的新样本，但是为了区别于“样本”，仍然采用“单元”来叙述。为了表示更加简洁，我们为这些单元统一下标，即第 $i$ 个单元为 $<h_i,s_i>$。

我们总共要训练出 $N$ 个最大熵模型，$N$ 为上面介绍的可能的状态数。每个单元的三元组 $h_i$ 中的前一个时刻状态总共有 $N$ 种取值，将相同取值的单元划分为同组，总共可以将单元分为 $N$ 组，每组单元训练一个最大熵模型，即每组单元对应一个权重向量。这些最大熵模型的训练方法类似，所以这里只讨论其中一组的训练方法。

假设这组单元对应的前一个时刻状态取值均为 $s^{\prime }$，单元个数为 $K_{s^{\prime }}$，对这组单元重新顺序编号为 $1\sim K_{s^{\prime }}$，那么这些单元对应的 $<h,s>$ 的下标也对应重新编号为 $1\sim K_{s^{\prime }}$。定义特征函数的经验期望：
$$E_{\tilde{P}}(f)=\frac{1}{K_{s^{\prime }}}\sum _{k=1}^{K_{s^{\prime }}}f(h_k,s_k)\text{\hspace{1em}(5)}$$
使用估计的条件概率计算的特征函数的真实期望：
$$\begin{array}{rl}{E}_P(f)& =\frac{1}{K_{s^{\prime }}}\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^{N}P(s=q_i\mid s^{\prime },h_k)f(h_k,s=q_i)\\ & =\frac{1}{K_{s^{\prime }}}\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)f(h_k,s=q_i)\end{array}\text{\hspace{1em}(6)}$$
最大熵模型对应优化问题的约束条件（之一）为
$$E_{\tilde{P}}(f_i)=E_P(f),i=1,2,\dots ,n$$
其中 $n$ 为特征函数个数。最大熵模型的学习转化为约束最优化问题，优化问题对应的目标函数为
$$\underset{P_{s^{\prime }}}{\max }H(P_{s^{\prime }})=-\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(h_k)P_{s^{\prime }}(s=q_i\mid h_k)\log P_{s^{\prime }}(s=q_i\mid h_k)$$
由于枚举的单元都是被观察到的单元，所以 $P_{s^{\prime }}(h_k)=1$。故，完整的约束优化问题为
$$\begin{array}{lc}\underset{P_{s^{\prime }}}{\max }& H(P_{s^{\prime }})=-\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\log P_{s^{\prime }}(s=q_i\mid h_k)\\ s.t.& K_{s^{\prime }}{E}_P(f_i)=K_{s^{\prime }}{E}_{\tilde{P}}(f_i),i=1,2,\dots ,n\\ & \sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)=K_{s^{\prime }}\end{array}$$
转换为最小化问题后对应的拉格朗日函数为
$$\begin{array}{rl}L(P_{s^{\prime }},w)& =-H(P_{s^{\prime }})+w_0(K_{s^{\prime }}-\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k))+K_{s^{\prime }}\sum _{i=1}^n{w}_i(E_{\tilde{P}}(f_i)-E_P(f_i))\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\log P_{s^{\prime }}(s=q_i\mid h_k)+w_0(K_{s^{\prime }}-\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k))+\sum _{i=1}^n{w}_i\sum _{k=1}^{K_{s^{\prime }}}(f_i(h_k,s_k)-\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)f_i(h_k,s=q_i))\end{array}$$
拉格朗日函数对 $P_{s^{\prime }}(s\mid h)$ 求偏导，其中 $s$ 和 $h$ 均为确切取值，假设这 $K_{s^{\prime }}$ 个单元中为 $<h,s>$ 的单元个数为 $K$，则
$$\frac{\partial L}{\partial P_{s^{\prime }}(s\mid h)}=K(\log P_{s^{\prime }}(s\mid h)+1)-K{w}_0-K\sum _{i=1}^N{w}_i{f}_i(h,s)$$
令偏导为零，利用 $\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h)$ 可得最大熵模型
$$P_{s^{\prime }}(s\mid h)=\frac{\exp (w\cdot f(h,s))}{Z(h,s^{\prime })}\text{\hspace{1em}(7)}$$
其中
$$Z(h,s^{\prime })=\sum _{i=1}^N\exp (w\cdot f(h,s=q_i))$$
其中 $w\cdot f$ 为向量内积。

将式 $(7)$ 代入拉格朗提函数得到对偶函数
$$\begin{array}{rl}\psi (w)& =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\log P_{s^{\prime }}(s=q_i\mid h_k)+\sum _{i=1}^n{w}_i\sum _{k=1}^{K_{s^{\prime }}}(f_i(h_k,s_k)-\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)f_i(h_k,s=q_i))\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\log P_{s^{\prime }}(s=q_i\mid h_k)+\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)-\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\sum _{i=1}^n{w}_i{f}_i(h_k,s=q_i)\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)+\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\log P_{s^{\prime }}(s=q_i\mid h_k)-\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\sum _{i=1}^n{w}_i{f}_i(h_k,s=q_i)\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)+\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)(\log P_{s^{\prime }}(s=q_i\mid h_k)-\sum _{i=1}^n{w}_i{f}_i(h_k,s=q_i))\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)-\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\log Z(h_k,s^{\prime })\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)-\sum _{k=1}^{K_{s^{\prime }}}\log Z(h_k,s^{\prime })\sum _{i=1}^N{P}_{s^{\prime }}(s=q_i\mid h_k)\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)-\sum _{k=1}^{K_{s^{\prime }}}\log Z(h_k,s^{\prime })\end{array}$$
这里的最大熵模型同样满足对偶函数与对数似然函数等价。对数似然函数为
$$\begin{array}{rl}L(w)& =\log \prod _{k=1}^{K_{s^{\prime }}}{P}_{s^{\prime }}(s_k\mid h_k)\\ & =\sum _{k=1}^{K_{s^{\prime }}}\log P_{s^{\prime }}(s_k\mid h_k)\\ & =\sum _{k=1}^{K_{s^{\prime }}}\left(\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)-\log Z(h_k,s^{\prime })\right)\\ & =\sum _{k=1}^{K_{s^{\prime }}}\sum _{i=1}^n{w}_i{f}_i(h_k,s_k)-\sum _{k=1}^{K_{s^{\prime }}}\log Z(h_k,s^{\prime })\end{array}$$
可见，对数似然函数与对偶函数相同。

极大化 $\psi (w)$ 可以采用最大熵模型中提到的最优化算法，比如通用迭代尺度法（GIS）、改进的迭代尺度法（IIS）等。文献 [3] 中介绍到，对每组单元对应的 $\psi (w)$ 分别采用 GIS 进行迭代，最终得到 $N$ 组权重向量，对应 $N$ 个最大熵模型，这 $N$ 个最大熵模型完整地描述了概率分布 $P(s\mid s^{\prime },h)$。

可以想象，如果满足二阶马尔可夫性，那么就需要训练 $N\times N$ 个最大熵模型来描述概率分布 $P(s\mid s^{\prime },s^{\prime \prime },h)$，具体过程与上面类似。

对比两个文献提出的学习方法，文献 [1] 的观点更能让我信服，而且可以通过比较合理的推导进行证明。

这部分推导属于我自己研究的，正确性无法保证，仅供参考。

解码问题

Daniel Jurafsky 在《Speech and Language Processing》中提到，MEMM 的解码也可以采用类似于 HMM 中近似算法的贪心思想。使用这种方式解码，需要对输入观测序列从头到尾运行分类器，每次分类都作出当前最好的决定。算法流程大致描述为，从头到尾扫描整个观测序列，对于每个时刻，根据前一个时刻我们的解码得到的状态选择当前时刻对应的最大熵模型学习到的条件概率分布来确定当前时刻的解码状态，依次类推。特别地，第一个时刻的解码状态可以仅依赖于观测。

至于 Viterbi 算法也是与 HMM 一致。定义
$${\delta }_t(i)=\underset{s_1,s_2,\dots ,s_{t-1}}{\max }P(O,s_t=q_i,s_{t-1},\dots ,s_1\mid w),1\le i\le N$$
其中 $P$ 是 $P_{s^{\prime }}$ 的简写。对式 $(1)$ 变形可得
$$\begin{array}{rl}{\delta }_t(i)& =\underset{s_1,s_2,\dots ,s_{t-1}}{\max }P(s_t=q_i\mid s_{t-1},\dots ,s_1,O,w)P(s_{t-1},\dots ,s_1,O\mid w)\\ & =\underset{1\le j\le N}{\max }P(s_t=q_i\mid h_t,w){\delta }_{t-1}(j)\\ & =\underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)]P(s_t=q_i\mid h_t,w)\end{array}$$
如果考虑一阶马尔可夫性，那么其中 $h_t=<s_{t-1},O,t>$。初始化
$${\delta }_1(i)=P(s_1=q_i\mid h_1,w)$$
其中 $h_1=<O,1>$。

定义在时刻 $t$ 状态为 $q_i$ 的所有单个路径 $(s_1,s_2,\dots ,s_{t-1},s_t=q_i)$ 中概率最大的路径的第 $t-1$ 个结点为
$${\psi }_t(i)=\arg \underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)],,1\le i\le N$$
${\psi }_t(i)$ 保存的是时刻 $t$ 状态 $s_t=q_i$ 由时刻 $t-1$ 的哪种状态转移而来。初始化
$${\psi }_1(i)=0$$
终止
$$\begin{gathered} P^{\ast }=\underset{1\le i\le N}{\max }{\delta }_T(i) \\ {s}_T^{\ast }=\arg \underset{1\le i\le N}{\max }[{\delta }_T(i)] \end{gathered}$$
路径回溯，只需要根据 $s_t^{\ast }={\psi }_{t+1}(s_{t+1}^{\ast })$ 逆序递推即可得到最优路径 $S^{\ast }=(s_1^{\ast },s_2^{\ast },\dots ,s_T^{\ast })$。

关于“双向 MEMM”、“MEMM 的缺点”等扩展问题在这里不展开，可以见其他文章。

REF

[1] McCallum A, Freitag D, Pereira F C N. Maximum entropy Markov models for information extraction and segmentation[C]//Icml. 2000, 17(2000): 591-598.

[2] Ratnaparkhi A. A maximum entropy model for part-of-speech tagging[C]//Conference on empirical methods in natural language processing. 1996.

[3] fall2014-loglineartaggers.pdf (columbia.edu)

[4] Collins M. Log-linear models[J]. Self-published Tutorial, 2005.

[5] Collins M. Log-linear models, memms, and crfs[J]. Columbia University lecture, 2015.

[6] Lafferty J, McCallum A, Pereira F C N. Conditional random fields: Probabilistic models for segmenting and labeling sequence data[J]. 2001.

[7] Wang H, Fei H, Yu Q, et al. A motifs-based Maximum Entropy Markov Model for realtime reliability prediction in System of Systems[J]. Journal of Systems and Software, 2019, 151: 180-193.

[8]《Speech and Language Processing》Daniel Jurafsky 等著

[9]《百面机器学习》诸葛越等著

[10] 【机器学习】最大熵模型【上】最大熵模型概述与约束最优化问题 - CSDN

[11] 【机器学习】最大熵模型【下】最大熵模型学习的最优化算法 - CSDN

[12] 【自然语言处理】隐马尔可夫模型【Ⅴ】解码问题 - CSDN

[13] (【自然语言处理】隐马尔可夫模型【Ⅱ】隐马尔科夫模型概述 - CSDN