有一个正 $n$ 边形，每个点的颜色为红色，蓝色，绿色中的其中一种。保证每种颜色至少出现一次且 $n$ 边形上相邻的两个点颜色不同。你想要连接 $n-3$ 条对角线，使得对角线把整个图形分成了 $n-2$ 个三角形（即三角剖分），并且每个三角形三个顶点颜色两两不同。任意输出一种方案即可，如果无解输出 Impossible!

$n\le 10^6$

如果某种颜色在 $n$ 个点中只出现一次，那么所有三角形都有这个颜色所在的点，所以只能把这个点连向所有其他点，判断是否可行。

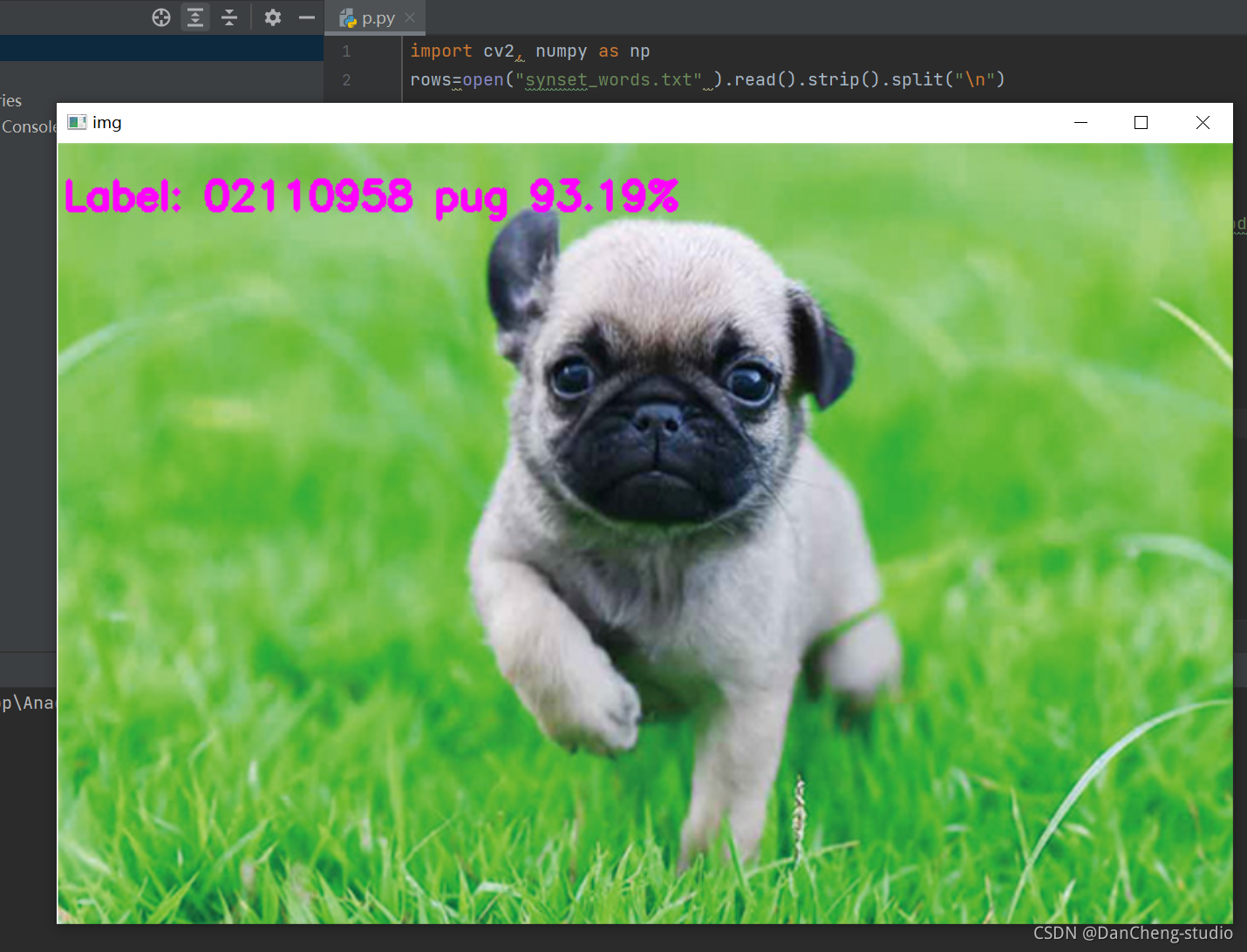
考虑 $n^2$ 的暴力。枚举 $j,k$，那么由三个点 $1,j,k$ 构成的三角形把多边形分成了外面的三份（下面的三角形顶点颜色都符合条件）。看下图，点 $1,4,9$ 所构成的三角形把这个十边形分成红色 $1,2,3$ 三份

然后考虑每一份的情况，设有边相连的点为 $l,r$，在一个块中枚举 $x$，由三个点 $l,r,x$ 构成的三角形把这个块分成两份。图中点 $4,6,9$ 构成的三角形把块分成蓝色 $1,2$ 两部分，发现这里分下去形式相同，所以这里可以递归下去，再加一个记忆化，$f_{i,j}$ 表示从点 $i$ 到 $j$ 的块是否能三角剖分，这样的时间复杂度是 $O(n^2)$ 的。

由于这样分下去最终一定会无法再分，说明若有解，在多边形上必有连续三个顶点颜色互不相同（它们构成的三角形是无法再分的）。这时把中间的点删去（因为这个点后面不会再用到），这样变成了 $n-1$ 边形，这样就可以递归考虑下去，不停的删点，如果点数大于三但是不能再删下去就是无解。这样操作的前提是任意颜色数量都大于 $1$，因为如果把只剩一种颜色的点删去了，本来可能有解，被你搞成无解了。
这时候还有一个问题，有没有可能找到了三个连续定点，删去中间这个就不行了，而选其他的三个删中间的就行了？其实不会，如果删去的点的颜色数量只剩两个，假设这两个点“删去”了，那么现在相邻两个点颜色要互异，否则无解，跟删哪个点没有关系；如果有删去的点的颜色数量有很多，由归纳法得知任意删去一个即可。

实现上可以用链表来维护点。时间复杂度 $O(n)$。

代码如下

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+1;
int n,bj[N],num[3];
char s[N];
int head,nxt[N],pre[N],col[N],cnt,sz;
vector<pair<int,int> > ans;
void dfs(int now)
{
    if(sz==3||bj[now]) return;
    if(num[0]==1||num[1]==1||num[2]==1){
        int now=head;
        for(int i=1;i<=sz;i++){
            if(num[col[now]]==1) break;
            now=nxt[now];
        }
        int i=nxt[now];
        for(;nxt[i]!=now;i=nxt[i]){
            if((col[now]^col[i]^col[nxt[i]])!=3) cout<<"Impossible!",exit(0);
            if(i!=nxt[now]) ans.push_back(make_pair(now,i));
        }
        for(auto i:ans) cout<<i.first<<" "<<i.second<<"\n";
        exit(0);
    }
    if(col[pre[now]]^col[nxt[now]]^col[now]==3){
        ans.push_back(make_pair(pre[now],nxt[now]));
        bj[now]=1;
        num[col[now]]--;
        nxt[pre[now]]=nxt[now];
        pre[nxt[now]]=pre[now];
        head=nxt[now];
        sz--;
        dfs(pre[now]);
        dfs(nxt[now]);
    }
}
int main()
{
    freopen("polygon.in","r",stdin);
    freopen("polygon.out","w",stdout);
    cin.tie(0)->sync_with_stdio(0);
    cin>>n>>(s+1);
    head=1;
    for(int i=1;i<=n;i++){
        num[s[i]=='R'?0:s[i]=='G'?1:2]++;
        col[++cnt]=(s[i]=='R'?0:s[i]=='G'?1:2);
        pre[cnt]=cnt-1;
        nxt[cnt-1]=cnt;
    }
    nxt[cnt]=1;
    pre[1]=cnt;
    if(!num[0]||!num[1]||!num[2]) goto a;
    sz=n;
    for(int i=1;i<=n;i++) dfs(i);
    a:cout<<"Impossible!";
}