近日，阿里云人工智能平台 PAI与华东师范大学陈岑副教授团队合作在深度学习顶级会议 CIKM 2023 上发表 OLSS (Optimal Linear Subspace Search) 算法，这是一种针对扩散模型的采样加速算法。在这篇论文中，扩散模型加速算法的本质被建模成线性子空间的扩张过程，给出了目前方法的统一分析，并基于此设计了新的加速算法，大幅度提升了扩散模型的生成速度。

论文：

Zhongjie Duan, Chengyu Wang, Cen Chen, Jun Huang, Weining Qian. Optimal Linear Subspace Search: Learning to Construct Fast and High-Quality Schedulers for Diffusion Models. CIKM 2023

背景

近年来，在图像生成领域，对于扩散模型的成功我们有目共睹。与基于 GAN 的生成模型不同，扩散模型需要多次调用模型进行前向推理，经过多次迭代，才能得到清晰完整的图像。扩散模型在大幅度提升生成效果的同时，也因其迭代式的生成过程面临严重的计算效率问题。我们希望改进扩散模型的生成过程，减少迭代步数，提升生成速度。

加速算法的统一分析

形式化地，给定一个扩散模型${ϵ}_{\theta }$，在一次完整的生成过程中从高斯噪声 ${\mathbf{x}}_T$开始，经过 $T$ 步采样，依次得到${\mathbf{x}}_{T-1},\dots ,{\mathbf{x}}_0$。为了保证生成效果，$T$ 在训练时通常被设置的非常大，例如 Stable Diffusion 中是 $1000$。现有的一些研究工作提出了“调度机”（scheduler）的概念。一个调度机会在 { T , T − 1 , … , 0 } \{T,T-1,\dots,0\} {T,T−1,…,0} 中取出一个 $n$ 步递减的子序列 $t(1),\dots ,t(n)$，只在这 $n$步中调用模型进行前向推理，构建完整生成过程的近似过程，重构出迭代公式。

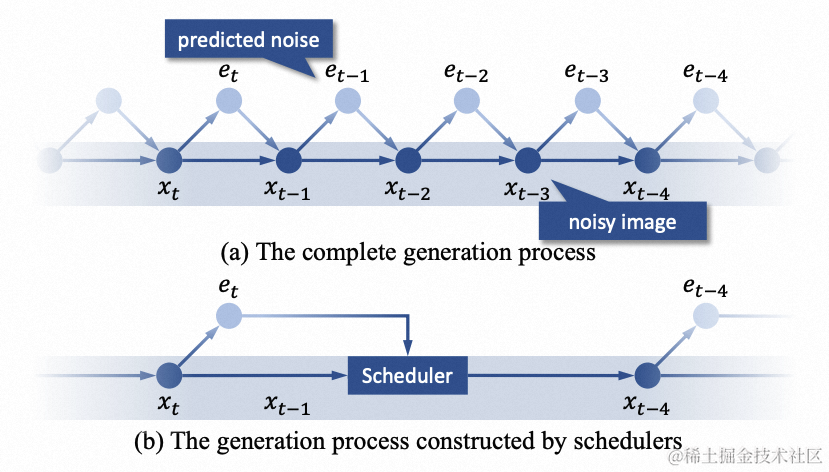
具体地，在 DDIM 调度机中

$${\mathbf{x}}_{t(i+1)}=\sqrt{{\alpha }_{t(i+1)}}\left(\frac{{\mathbf{x}}_{t(i)}-\sqrt{1-{\alpha }_{t(i)}}{\mathbf{e}}_{t(i)}}{\sqrt{{\alpha }_{t(i)}}}\right)+\sqrt{1-{\alpha }_{t(i+1)}}{\mathbf{e}}_{t(i)}.$$

其中${\mathbf{e}}_{t(i)}$ 是模型的输出值。在一些基于常微分方程的调度机中，$x_t$ 被建模成步骤$ t$ 的函数，进而可以使用常微分方程的数值近似算法——前向欧拉方法求解

$${\mathbf{x}}_{t(i+1)}={\mathbf{x}}_{t(i)}+(t(i+1)-t(i))\frac{\mathrm{d}{\mathbf{x}}_{t(i)}}{\mathrm{d}t(i)},$$

其中

$$\frac{\mathrm{d}{\mathbf{x}}_t}{\mathrm{d}t}=-\frac{\mathrm{d}{\alpha }_t}{\mathrm{d}t}\left(\frac{{\mathbf{x}}_t}{2{\alpha }_t}-\frac{{\mathbf{e}}_t}{2{\alpha }_t\sqrt{1-{\alpha }_t}}\right).$$

PNDM 调度机则是基于线性多步方法构造了一个伪数值近似算法

$${\mathbf{x}}_{t(i+1)}=\frac{\sqrt{{\alpha }_{t(i+1)}}}{\sqrt{{\alpha }_{t(i)}}}{\mathbf{x}}_{t(i)}-\frac{1}{\sqrt{{\alpha }_{t(i)}}}{\alpha }_{t(i)}^{\prime }{\mathbf{e}}_{t(i)}^{\prime },$$

其中

$${\mathbf{e}}_{t(i)}^{\prime }=\frac{1}{24}(55{\mathbf{e}}_{t(i)}-59{\mathbf{e}}_{t(i-1)}+37{\mathbf{e}}_{t(i-2)}-9{\mathbf{e}}_{t(i-3)}),$$

$${\alpha }_{t(i)}^{\prime }=\frac{{\alpha }_{t(i+1)}-{\alpha }_{t(i)}}{\sqrt{(1-{\alpha }_{t(i+1)}){\alpha }_{t(i)}}+\sqrt{(1-{\alpha }_{t(i)}){\alpha }_{t(i+1)}}}.$$

观察以上调度机中的迭代公式，我们不难发现
x t ( i + 1 ) ∈ span { x t ( i ) , e t ( 1 ) , … , e t ( i ) } . \boldsymbol x_{t(i+1)}\in\text{span}\{\boldsymbol x_{t(i)},\boldsymbol e_{t(1)},\boldsymbol \dots,\boldsymbol e_{t(i)}\}. xt(i+1)​∈span{xt(i)​,et(1)​,…,et(i)​}.

用数学归纳法易证

x t ( i + 1 ) ∈ span { x t ( 1 ) , e t ( 1 ) , … , e t ( i ) } . \boldsymbol x_{t(i+1)}\in\text{span}\{\boldsymbol x_{t(1)},\boldsymbol e_{t(1)},\boldsymbol \dots,\boldsymbol e_{t(i)}\}. xt(i+1)​∈span{xt(1)​,et(1)​,…,et(i)​}.

这其实揭示了调度机设计的本质——在由模型输出值和初始高斯噪声张成的向量空间中求解下一步的${\mathbf{x}}_T$。不同的调度机仅在迭代公式的系数上存在不同，我们决定设计一个新的调度机，将迭代公式中的系数设计成可训练的，使其对应的近似计算过程更加精确。

算法架构

假定$n$个步骤 { t ( 1 ) , … , t ( n ) } \{t(1),\dots,t(n)\} {t(1),…,t(n)} 已经被选出，在第 $i$ 步，我们已经得到了 ${\mathbf{x}}_{t(1)},\dots ,{\mathbf{x}}_{t(i)}$ 以及${\mathbf{e}}_{t(1)},\dots ,{\mathbf{e}}_{t(i)}$，考虑计算 ${\mathbf{x}}_{t(i+1)}$ 的近似值 ${\hat{\mathbf{x}}}_{t(i+1)}$，根据我们上文中的分析，${\hat{\mathbf{x}}}_{t(i+1)}$ 应当在由 { x t ( 1 ) , e t ( 1 ) , … , e t ( i ) } \{\boldsymbol x_{t(1)},\boldsymbol e_{t(1)},\boldsymbol \dots,\boldsymbol e_{t(i)}\} {xt(1)​,et(1)​,…,et(i)​} 张成的线性子空间中求解，即

$${\hat{\mathbf{x}}}_{t(i+1)}=w_{i,0}{\mathbf{x}}_{t(1)}+\sum _{j=1}^i{w}_{i,j}{\mathbf{e}}_{t(j)}.$$

为了确定最佳的参数 { w i , j } \{w_{i,j}\} {wi,j​}，我们需要对其进行训练。考虑到训练参数较少，我们并不采用基于梯度的训练方法，而是直接使用最小二乘法求最优解。首先采集来自完整生成过程的变量${\mathbf{x}}_{t(i+1)}$，令损失函数 $\mathcal{L}=||{\hat{\mathbf{x}}}_{t(i+1)}-{\mathbf{x}}_{t(i+1)}|{|}_2^2$，使用基于 QR 分解的最小二乘求解算法，在保证数值稳定性的前提下计算出最优参数，构成新的调度机算法。我们称这个新的调度机算法为 OLSS (Optimal Linear Subspace Search)。

我们在下图中提供了这个过程的几何解释，在完整生成过程中 x t − 1 ∈ span { x t , e t } \boldsymbol x_{t-1}\in\text{span}\{\boldsymbol x_t, \boldsymbol e_t\} xt−1​∈span{xt​,et​}；由 DDIM 调度机构造的近似过程中，若跳过${\mathbf{x}}_t$，那么$\hat{\mathbf{x}}\ast t-1\in \text{span}\mathbf{x}\ast t+1,\mathbf{e}\_t+1；$而在由 OLSS 构造的近似过程中，若跳过 ${\mathbf{x}}_t$，则在一个更高维线性子空间 span { x T , e T , … , e t + 1 } \text{span}\{\boldsymbol x_T,\boldsymbol e_T,\dots,\boldsymbol e_{t+1}\} span{xT​,eT​,…,et+1​}中计算${\hat{\mathbf{x}}}_{t-1}$，具有更低的误差

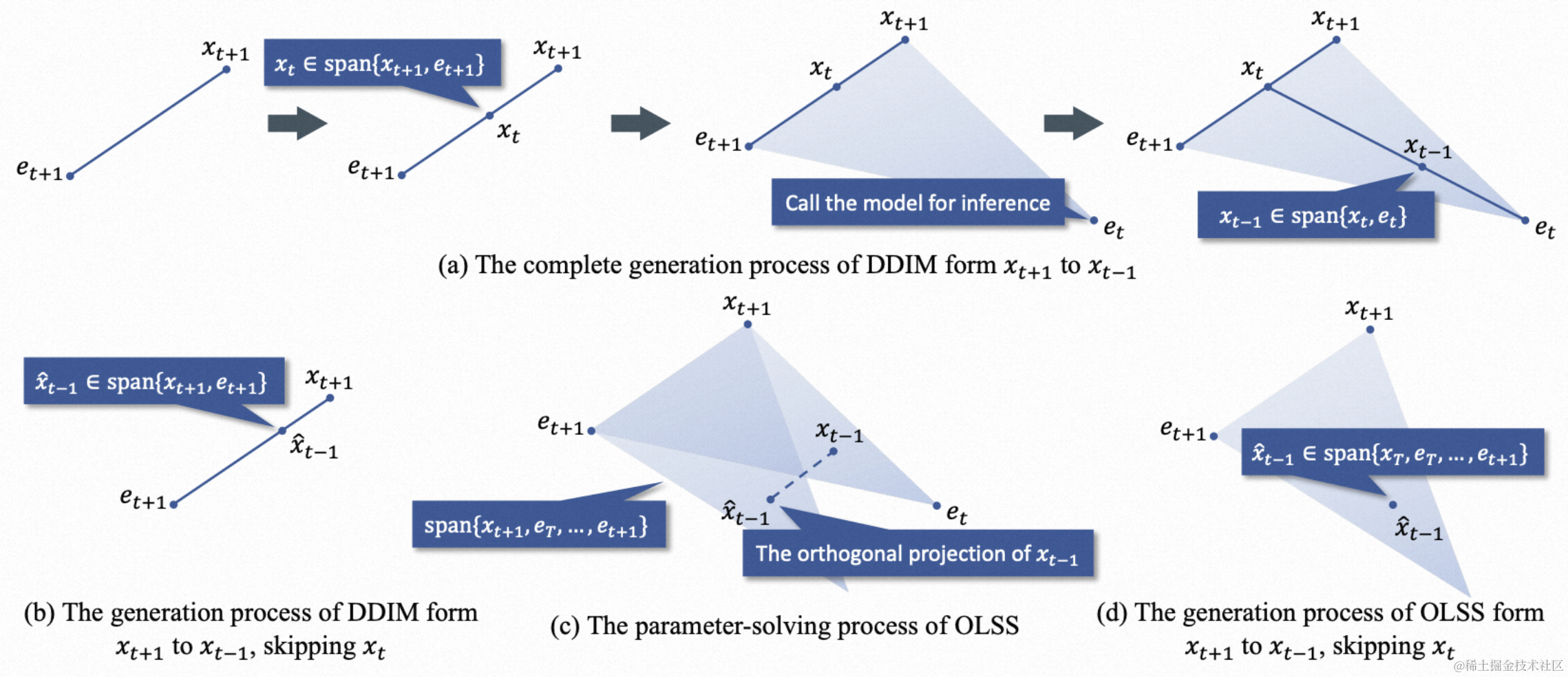
此外，为了进一步降低这个算法的误差，我们还对 { t ( 1 ) , … , t ( n ) } \{t(1),\dots,t(n)\} {t(1),…,t(n)} 进行了调整。具体地，设计了一个启发式的路径规划算法，分为以下三部分：

其中算法 1 利用贪心策略搜索下一步的 $t(i)$，算法 2 调用算法 1 搜索在误差上届 $D$ 下是否存在这样的路径，算法 3 调用算法 2 搜索最低的误差上界。整个路径规划算法可以使 $n$ 步中的最大误差最小。

实验结果

我们在主流的 Stable Diffusion 1.4 和 Stable Diffusion 2.1 上进行了实验，测试了包括 OLSS 和 OLSS-P（无路径规划版本）在内的 8 个调度机算法，使用 5 步、10 步、20 步的算法与 100 步、1000 步的算法比较，FID 结果（越小越好）如下表所示：

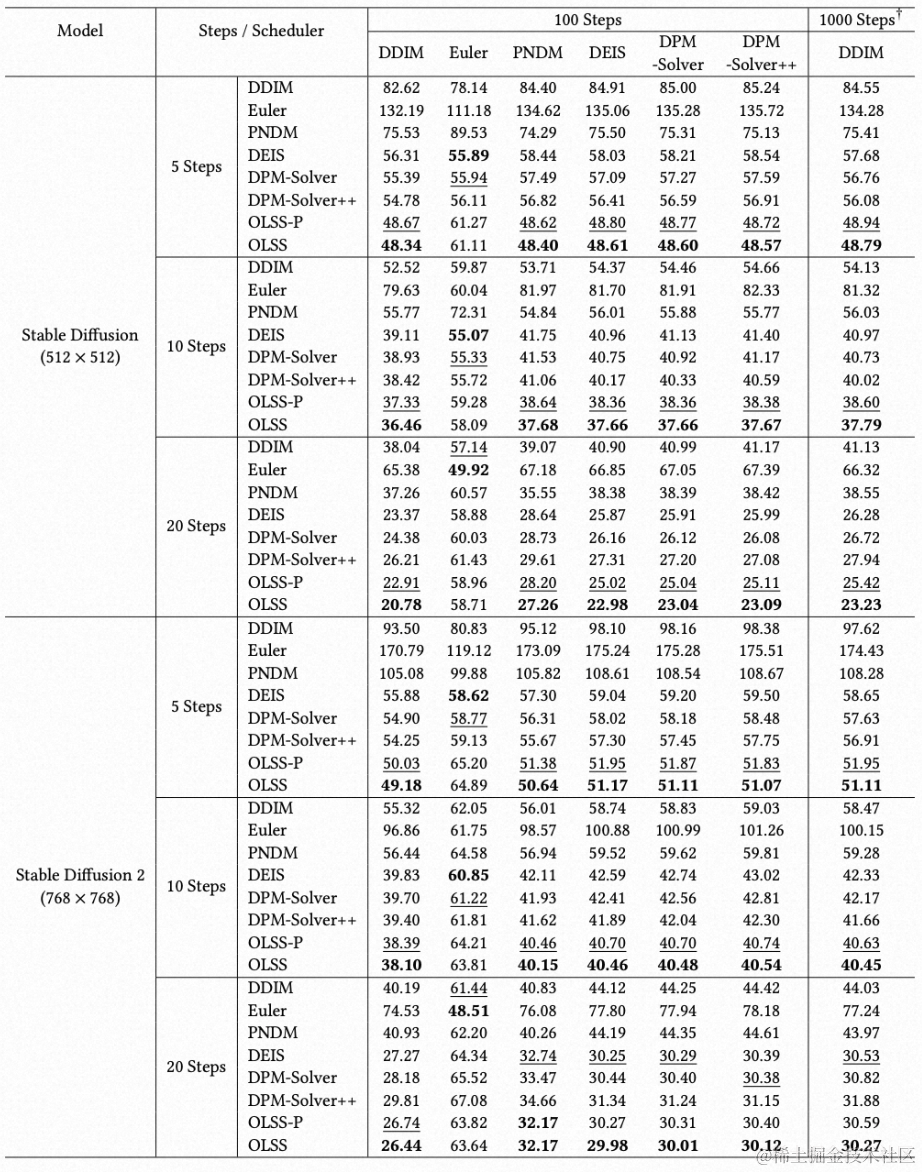
我们可以明显看出，在同等步数下，OLSS 比其他调度机算法能够实现更高的图像质量，这证明了 OLSS 方法的巨大优越性。此外，从以下例子中我们也可以明显看出 OLSS 在极少步数下的效果：

目前 OLSS 已经在 EasyNLP（https://github.com/alibaba/EasyNLP/tree/master/diffusion/olss_scheduler）开源。欢迎广大用户试用！

参考文献

• Bingyan Liu, Weifeng Lin, Zhongjie Duan, Chengyu Wang, Ziheng Wu, Zipeng Zhang, Kui Jia, Lianwen Jin, Cen Chen, Jun Huang. Rapid Diffusion: Building Domain-Specific Text-to-Image Synthesizers with Fast Inference Speed. In the 61st Annual Meeting of the Association for Computational Linguistics (Industry Track).
• Chengyu Wang, Minghui Qiu, Taolin Zhang, Tingting Liu, Lei Li, Jianing Wang, Ming Wang, Jun Huang, Wei Lin. EasyNLP: A Comprehensive and Easy-to-use Toolkit for Natural Language Processing. In the 2022 Conference on Empirical Methods in Natural Language Processing (Demo Track).
• Jiaming Song, Chenlin Meng, and Stefano Ermon. 2020. Denoising Diffusion Implicit Models. In International Conference on Learning Representations.
• Tero Karras, Miika Aittala, Timo Aila, and Samuli Laine. 2022. Elucidating the design space of diffusion-based generative models. Advances in Neural Information Processing Systems 35 (2022), 26565–26577.
• Luping Liu, Yi Ren, Zhijie Lin, and Zhou Zhao. 2021. Pseudo Numerical Methods for Diffusion Models on Manifolds. In International Conference on Learning Representations.
• Qinsheng Zhang and Yongxin Chen. 2022. Fast Sampling of Diffusion Models with Exponential Integrator. In The Eleventh International Conference on Learning Representations.
• Cheng Lu, Yuhao Zhou, Fan Bao, Jianfei Chen, Chongxuan Li, and Jun Zhu. 2022. Dpm-solver: A fast ode solver for diffusion probabilistic model sampling in around 10 steps. Advances in Neural Information Processing Systems 35 (2022), 5775–5787.
• Cheng Lu, Yuhao Zhou, Fan Bao, Jianfei Chen, Chongxuan Li, and Jun Zhu. 2022. Dpm-solver++: Fast solver for guided sampling of diffusion probabilistic models. arXiv preprint arXiv:2211.01095 (2022).

论文信息

论文标题：Optimal Linear Subspace Search: Learning to Construct Fast and High-Quality Schedulers for Diffusion Models
论文作者：段忠杰、汪诚愚、陈岑、黄俊、钱卫宁
论文pdf链接：https://arxiv.org/abs/2305.14677