一、本周周赛总结

• 都挺难的。
• T1dp。
• T2哈希+排序。
• T3容斥+二分。
• T4排列组合模板题。

二、 [Easy] 6273. 最多可以摧毁的敌人城堡数目

链接: 6273. 最多可以摧毁的敌人城堡数目

1. 题目描述

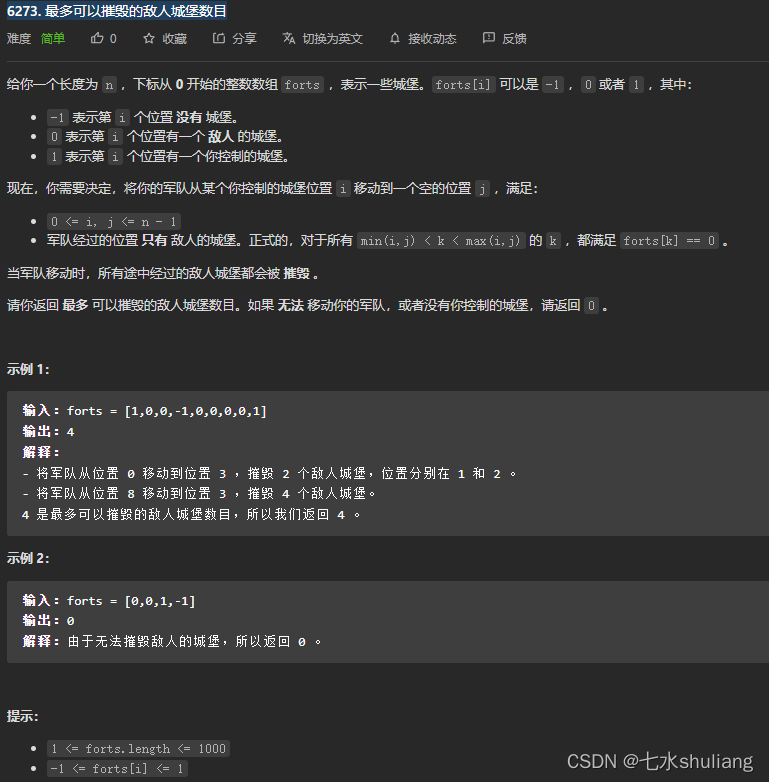
2. 思路分析

• dp计算出连续的0的个数。
• 然后遍历每个不为0的位置和计数:(i,v),显然这代表的连续0段的两个边界外界是l,r = [i-v,i+1]
• 当l和r合法，且分别是一个-1，1时则可更新ans
• 显然这等价于forts[l]*forts[r] == -1

3. 代码实现

class Solution:
    def captureForts(self, forts: List[int]) -> int:
        n = len(forts)
        f = [0]*n
        if forts[0] == 0:
            f[0] = 1
        for i in range(1,n):
            if forts[i] == 0:
                f[i] = f[i-1] + 1
        ans = 0
        for i,v in enumerate(f):
            l,r = i-v,i+1
            if l>=0 and r<n and forts[l]*forts[r] == -1:
                ans = max(ans,v)
        return ans

三、[Medium] 6274. 奖励最顶尖的 K 名学生

链接: 6274. 奖励最顶尖的 K 名学生

1. 题目描述

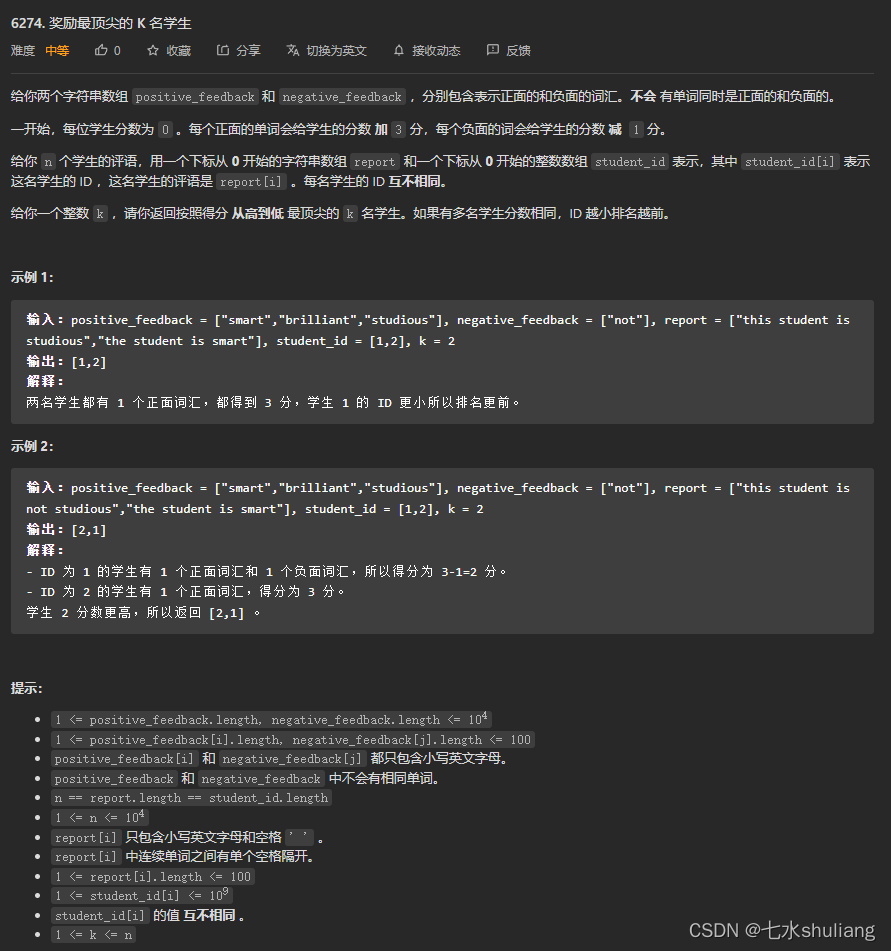
2. 思路分析

按题意模拟即可。

• 由于是python 因此直接split计算分数排序即可。
• 当然topk可以用小顶堆，但没必要。

3. 代码实现

class Solution:
    def topStudents(self, positive_feedback: List[str], negative_feedback: List[str], report: List[str], student_id: List[int], k: int) -> List[int]:
        ps = set(positive_feedback)
        ns = set(negative_feedback)
        ans = []
        for w,i in zip(report,student_id):
            p = 0
            for s in w.split():
                if s in ps:
                    p += 3
                elif s in ns:
                    p -= 1
            ans.append((-p,i))
        
        return [i for _,i in sorted(ans)[:k]]

四、[Medium] 6295. 最小化两个数组中的最大值

链接: 6295. 最小化两个数组中的最大值

1. 题目描述

2. 思路分析

• 最大值最小化=二分答案。
• 令函数ok(x)代表以x为最大值（答案）时，能否找到满足题意的元素。
• ok函数需要用容斥实现。1~x的x个元素分别分到4组里：同时被ab整除的数，仅能被a整除的数，仅能被b整除的数，不能被a或b整除的数。
• 那么显然arr1应该优先取仅能被b整除的数，然后取不能被整除的数，arr2同理。
• 当数不够取了，则无有效解，这个过程是O(1)的,但同时被整除的数由于要取lcm，是log。但lcm是固定的，可以预处理，因此还是O(1)
• 这个结果显然是单调的。
• 整体复杂度O(logn+log(max(a,b))),

3. 代码实现

class Solution:
    def minimizeSet(self, divisor1: int, divisor2: int, uniqueCnt1: int, uniqueCnt2: int) -> int:
        dd  = lcm(divisor1,divisor2)
        def ok(x):
            p1 = x // divisor1  # 能被d1整除
            p2 = x // divisor2  # 能被d2整除
            p3 = x // dd  # 能同时被d1,d2整除
            a = p1 - p3  # 仅能被d1整除
            b = p2 - p3  # 仅能被d2整除
            c = x - a-b-p3  # 不能被整除
            u1,u2 = uniqueCnt1,uniqueCnt2
            if u1>0:
                u1 -= b
            if u1>0:
                c -= u1
            if c < 0:
                return 0
            if u2>0:
                u2 -= a
            if u2>0:
                c -= u2
            if c < 0:
                return 0
            return 1

        return bisect_left(range(10**10),1,key=ok)

五、[Hard] 6276. 统计同位异构字符串数目

链接: 6276. 统计同位异构字符串数目

1. 题目描述

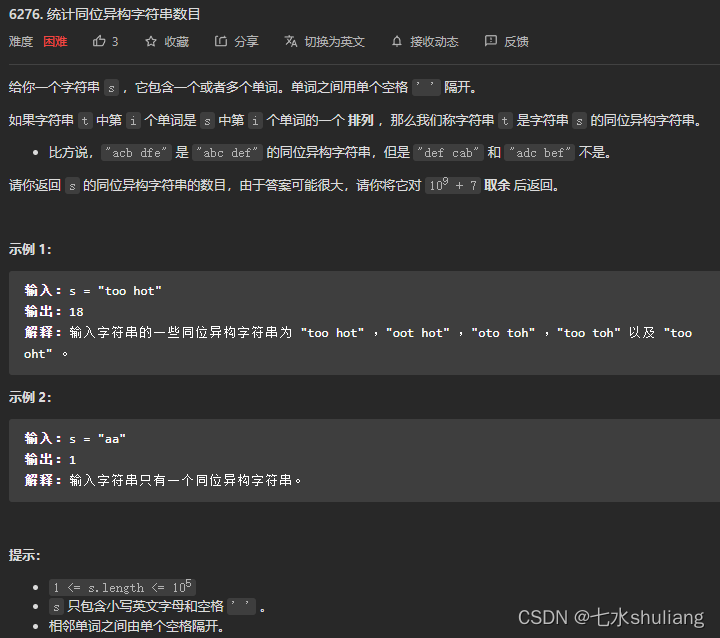
2. 思路分析

• 显然每个单词时独立的，可以计算每个单词的异构体数目，然后乘法原理即可。
• 如何计算呢？问题转化成如果计算含有重复元素的数组排列数。
• 假设长度n,含x种元素，分别计数为[c1,c2,c3…cx]。
• 放第一种c1个元素，考虑它们能选的位置有C(n,c1)个；然后放c2，显然从n-c1个位置里挑。
• 因此ans=C(n,c1) * C(n-c1,c2) * C(n-c1-c2,c3) * … * C(cx,cx)；另一种计算方法看代码。
• 这里整理成模板。

3. 代码实现

class ModComb:
    def __init__(self, n, p):
        """
        初始化，为了防止模不一样，因此不写默认值，强制要求调用者明示
        :param n:最大值，通常是2*(10**5)+50
        :param p: 模,通常是10**9+7
        """
        self.p = p
        self.inv_f, self.fact = [1] * (n + 1), [1] * (n + 1)  # 阶乘的逆元、阶乘
        inv_f, fact = self.inv_f, self.fact
        for i in range(2, n + 1):
            fact[i] = i * fact[i - 1] % p
        inv_f[-1] = pow(fact[-1], p - 2, p)
        for i in range(n, 0, -1):
            inv_f[i - 1] = i * inv_f[i] % p

    def comb(self, m, r):
        if m < r or r < 0:
            return 0
        return self.fact[m] * self.inv_f[r] % self.p * self.inv_f[m - r] % self.p

    def perm_count_with_duplicate(self, a):
        """含重复元素的列表a，全排列的种类。
        假设长度n,含x种元素，分别计数为[c1,c2,c3..cx]
        则答案是C(n,c1)*C(n-c1,c2)*C(n-c1-c2,c3)*...*C(cx,cx)
        或：n!/c1!/c2!/c3!/../cn!
        """
        ans = self.fact[len(a)]
        for c in Counter(a).values():
            ans = ans * self.inv_f[c] % self.p           
        return ans 
        # 下边这种也可以
        # s = len(a)
        # ans = 1
        # for c in Counter(a).values():
        #     ans = ans * self.comb(s,c) % MOD 
        #     s -= c
        # return ans 

MOD = 10  ** 9 + 7
class Solution:
    def countAnagrams(self, s: str) -> int:
        ret = 1
        mc = ModComb(len(s),MOD)      

        for w in s.split():
            ret = ret * mc.perm_count_with_duplicate(w) %MOD

        return (ret)%MOD

六、参考链接