基本原理

特征网络

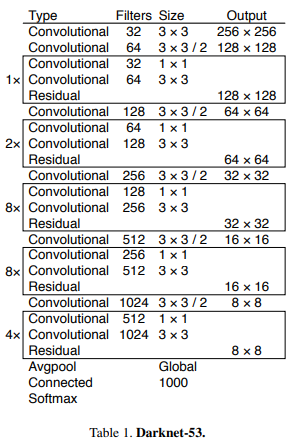
输入输出
输入$416\ast 416\ast 3$大小的图片（不唯一，但图片大小必为32的倍数），输出3个尺度的feature map,分别为$13\ast 13\ast 255$，$26\ast 26\ast 255$，$52\ast 52\ast 255$,即分成$13\ast 13$,$26\ast 26$,$52\ast 52$个grid cell.
每个grid cell生成3个anchor,每个anchor对应一个预测框，每个预测框有$5+80$个参数， { （ x , y , w , h , c ） , 80   k i n d s   o f   c l a s s } \{（x,y,w,h,c）,80 \space kinds \space of \space class\} {（x,y,w,h,c）,80 kinds of class}

输出分析
(该图取自知乎博主)

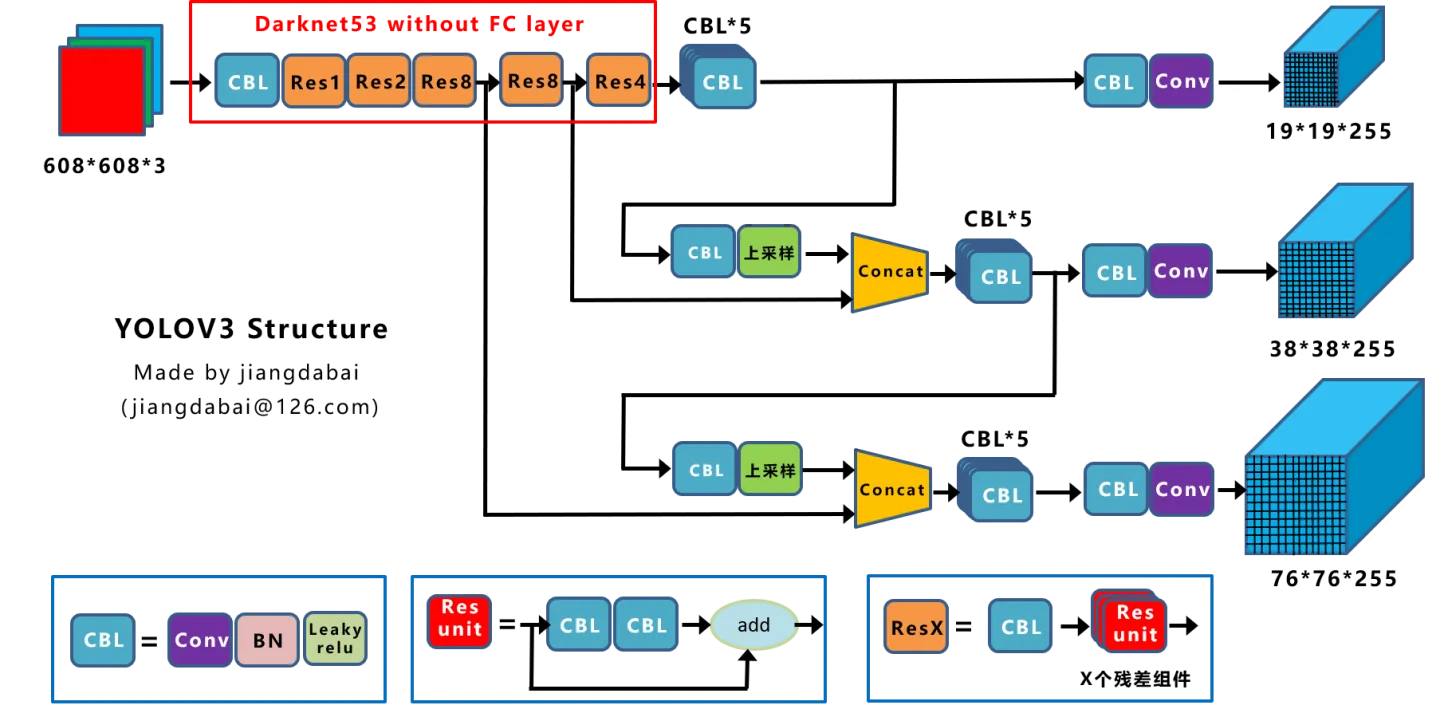
$13\ast 13\ast 255$，$26\ast 26\ast 255$，$52\ast 52\ast 255$分别预测大，中，小物体。
$13\ast 13\ast 255$为下采样32倍得到的特征；
$26\ast 26\ast 255$为下采样16倍与$13\ast 13$一次上采样结合得到的特征；
$52\ast 52\ast 255$为下采样8倍与$26\ast 26$一次上采样结合得到的特征；

正负样本
正样本为anchor与真实框的IOU大于指定阈值，且最大IOU的anchor；
负样本为anchor与真实框IOU小于指定阈值的anchor。

损失函数
由正样本的坐标损失、置信度损失和类别损失，负样本的置信度损失构成。
$$\begin{gathered} {\lambda }_{coord}\sum _{i=0}^{S^2}\sum _{J=0}^B{1}_{i,j}^{obj}[(b_x-\widehat{b_x}{)}^2+(b_y-\widehat{b_y}{)}^2+(b_w-\widehat{b_w}{)}^2+(b_h-\widehat{b_h}{)}^2] \\ +\sum _{i=0}^{S^2}\sum _{J=0}^B{1}_{i,j}^{obj}[-log(p_c)+\sum _{i=1}^{n}BCE(c_i,\widehat{c_i})] \\ +{\lambda }_{noobj}\sum _{i=0}^{S^2}\sum _{J=0}^B{1}_{i,j}^{noobj}[-log(1-p_c)] \end{gathered}$$
$S^2$为grid cell的总数，$B$为每一个grid cell的anchor数目。
第一行为计算正样本的坐标与真实框的坐标损失；
第二行为计算正样本的置信度和类别损失，$1_{i,j}^{obj}$表示是否为正样本；$-log(p_c)$中，若$p_c$越接近于1，则$-log(p_c)$越接近于0；类别损失中，对于检测的80类，每一个类别进行二叉熵损失运算。
第三行为负样本的置信度损失，$-log(1-p_c)$中$p_c$越接近于0，该式越小，接近于0

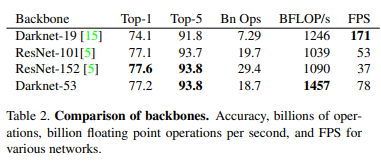
性能