一、什么是质数

质数也叫素数。如果一个大于等于2的整数，只能够被$1$和它本身整除，那么这个数就叫做质数。反之，这个数就称作合数。

二、质数的判断

1、试除法（朴素版）

试除法其实就是从定义出发，假设一个数$p$是质数，那么$p$就只能被1和$p$整除，那我就借此验证一下$p$是否能够被$2$ ~ $(p-1)$的数字整除。

bool prime(int  u)
{
	if(u<2)return false;
	for(int i=2;i<u;i++)
	{
		if(u%i==0)return false;
	}
	return true;
}

但是这种算法的时间复杂度是$O(n^2)$。这个时间复杂度是很高的。我们如何优化呢？

2、试除法（优化版）

假设$p$是一个合数，那么$p=a\ast b$，那么必定满足不等式：$a\le \sqrt{p}\le b$

---

证明：

如果$0<a<\sqrt{p}$ 同时 $0<b<\sqrt{p}$。那么$a\ast b<p$。

如果$a>\sqrt{p}$ 同时 $b>\sqrt{p}$，那么$a\ast b>p$。

因此，为了让$a\ast b=p$，只能是：$a\le \sqrt{p}\le b$

---

由于，我们只是想判断一个数是不是质数，所以我们只需要找到一个$2$ ~$(p-1)$的数能够整除$p$就行。因此我们只需要枚举$2$ ~$\sqrt{p}$。

bool prime(int  u)
{
	if(u<2)return false;
	for(int i=2;i<=u/i;i++)
	{
		if(u%i==0)return false;
	}
	return true;
}

此时代码的时间复杂度就是$O(\sqrt{n})$，时间上进行了极大的优化。

三、分解质因数

1、什么是质因数

如果$a$ % $b=0$，就说$b$是$a$的因数，如果这个因数又恰好是质数，那么就称$b$是$a$的质因数。

2、算术基本定理

任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积。

---

证明（反证法）

假设存在一个合数，其无法被分解为有限个质数的乘积，我们将这些数字放在一个集合中，那么这个集合中必存在一个最小的符合上述条件的合数$n$。

由于$n$是合数，所以必定存在$n=a\ast b$

由于$n$无法被分解成有限个质数的乘积，那么$a$和$b$必定不同时为质数。

$a$和$b$中至少存在一个合数，所以我们假设$a$是合数，$b$是质数。

由于我们的$n$是无法被分解成有限个质数中最小的一个，同时$a$一定是小于$n$的。所以$a$必定是可以分解为有限个质数的乘积的。即，$a=p_1^k\ast p_2^m\ast p_3^x...p_n^w$

那么此时我们的$n=b\ast p_1^k\ast p_2^m\ast p_3^x...p_n^w$

我们发现此时$n$被分解成了有限个质数，和我们的假设矛盾，所以原命题成立。

---

3、分解质因数

（1）问题

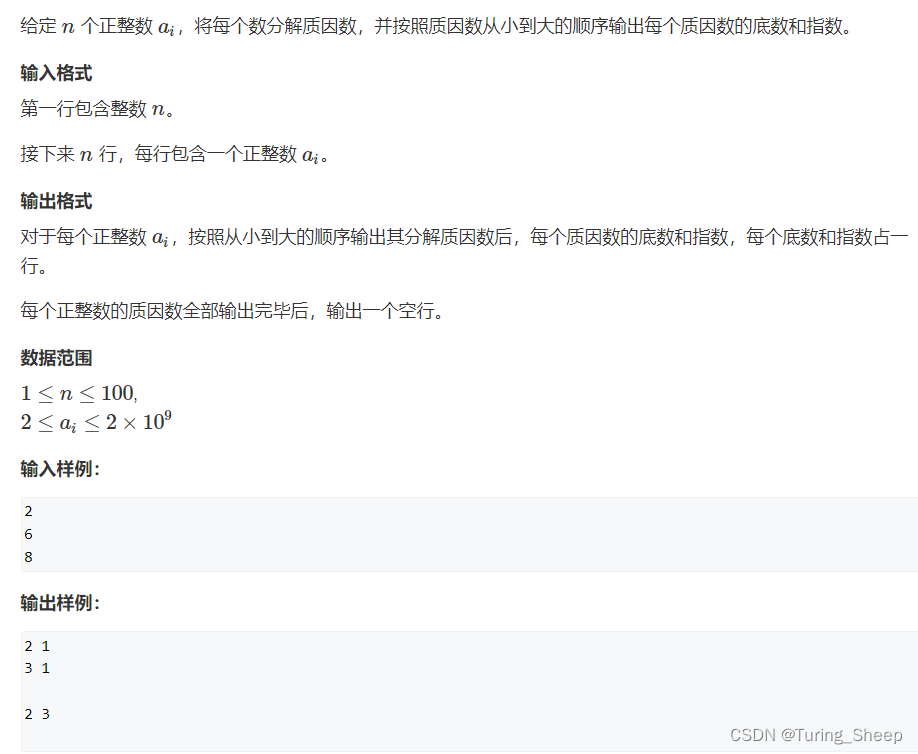
（2）思路

其实很简单，这道题就是考察我们怎么将一个合数写成算术基本定理的样子。
即$a=p_1^k\ast p_2^m\ast p_3^x...p_n^w$。

因此，我们需要先找到这个数的质因数$m$，这样我们就确定了底数，然后我们再不断地让$a/m$和 $a$%$m$。这样我们就能确定指数。

因为只要指数大于0，那么一定可以被整除，当指数降低为0以下的时候，此时就无法被整除了。

（3）代码

#include<iostream>
using namespace std;
int n;
void Prime_factor(int x)
{
    for(int i=2;i<=x;i++)
    {
        if(x%i==0)
        {
            int num=0;
            while(x%i==0)
            {
                num++;
                x/=i;
            }
            cout<<i<<" "<<num<<endl;
        }
    }
    puts("");
}
int main()
{
    cin>>n;
    while(n--)
    {
        int a=0;
        scanf("%d",&a);
        Prime_factor(a);
    }
    
}

（4）分析

n不断变化会漏解吗？

我们上述的代码中，直接把$i$当成了质因数，首先这个$i$能够整除$n$，所以它一定是因数。但是我们怎么确定这个数不是合数而是质数呢？

我们首先发现的第一件事其实应该是n是在不断变化的。每次都是去掉一个：$p_n^k$

所以我们先来思考一下，这样会不会漏解？
我们的$n=p_1^r\ast p_2^t\ast p_3^y...\ast p_n^u$，同时我们让$p_1,p_2,p_3...p_n$依次增大。

并且$p_1,p_2,p_3...p_n$都是大于等于2的整数，所以$n$一定是大于任何一个组成$n$的质数$p_n$

因为，$i$是从小到大依次枚举的，于是先枚举到的一定是$p_1$。当我们将$p_1^r$去掉后，此时的$n$记作$n_1$。$n_1=p_2^t\ast p_3^y...\ast p_n^u$

此时$i<p_2<p_3<...<p_n<n_1$，那么随着$i$从当前到$n_1$之间逐渐增大的时候，这些质数还是可以被枚举到的。

不会出现漏解的情况。

i一定是质因数？

假设我们存在一个合数$b$符合条件。由于$b$是合数，所以根据算数基本定理，
不妨再假设$b=p_1^q\ast p_2^w$

同时$p_1<b$，此时我们会先枚举到$p_1$。因为$b$能够整除$n$，所以$p_1$一定是能够整除$n$的。因此，$i=p_1$会优先出现。当出现这个质数的时候，我们会更新$n$，将$n$中的$p_1$删掉。

当$p_1$删掉后，此时的$n=p_2^w\ast p_3^y...\ast p_n^f$

很明显，此时更新后的$n$没有办法被$b$整除了（因为$n$中已经没有$p_1$这一项了），此时的合数$b$不满足条件，和假设矛盾。所以不存在这样的合数。

因此我们枚举到的$i$都是质因数。

（5）优化

一个数最多有一个$>\sqrt{n}$的质因数

证明很简单，还是和上次的证明方式相同。如果有两个，那么这个数已经是$>n$的了，不可能是$=n$的。

所以，我们可以利用$\sqrt{n}$来枚举，最后特判一下是否存在这样一个$>\sqrt{n}$的数。

#include<iostream>
using namespace std;
int n;
void Prime_factor(int x)
{
    for(int i=2;i<=x/i;i++)
    {
        if(x%i==0)
        {
            int num=0;
            while(x%i==0)
            {
                num++;
                x/=i;
            }
            cout<<i<<" "<<num<<endl;
        }
    }
    if(x>1)cout<<x<<" "<<1<<endl;
    puts("");
}
int main()
{
    cin>>n;
    while(n--)
    {
        int a=0;
        scanf("%d",&a);
        Prime_factor(a);
    }
    
}