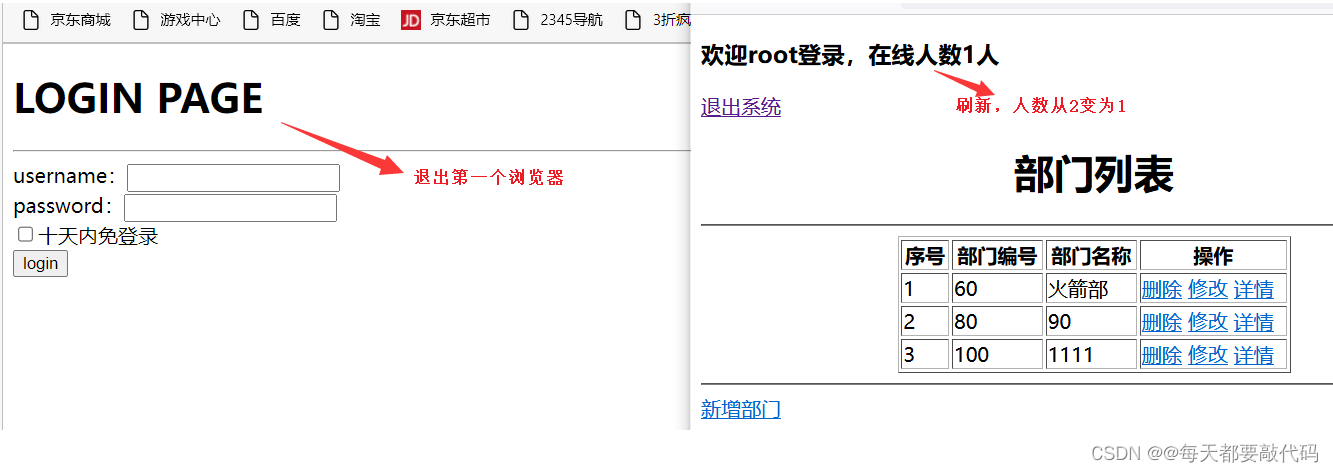
给定长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

1 x y，查询区间 [x,y] 中的最大连续子段和，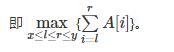

2 x y，把 A[x] 改成 y。
对于每个查询指令，输出一个整数表示答案。

输入格式
第一行两个整数 N,M。

第二行 N 个整数 A[i]。

接下来 M 行每行 3 个整数 k,x,y，k=1 表示查询（此时如果 x>y，请交换 x,y），k=2 表示修改。

输出格式
对于每个查询指令输出一个整数表示答案。

每个答案占一行。

数据范围
N≤500000,M≤100000,
−1000≤A[i]≤1000
输入样例：
5 3
1 2 -3 4 5
1 2 3
2 2 -1
1 3 2
输出样例：
2
-1

分析

1. 首先此题是单点修改，区间查询问题，只需要pushup函数即可，然后分析所查询的是最大连续字段和tmax，想求根节点的tmax，分三种情况：①tmax仅在分界线左边取得，那么根节点的u.tmax直接等于左儿子的tmax即可；②tmax仅在分界线右边取得，那么根节点的u.tmax直接等于右儿子的tmax即可；③根节点的tmax跨越分界线（横跨区间），那么u.tmax由左儿子的最大后缀和t[l].rmax + 右儿子的最大前缀和组成t[r].lmax；（最大后缀和：以区间右端点为终点，方向向左的最大后缀和；最大前缀和：以区间做左端点开始，方向向右的最大前缀和）每个结点（包括每一个儿子）都有lmax,rmax； 所以根节点的tmax就是上面三种情况的max值；

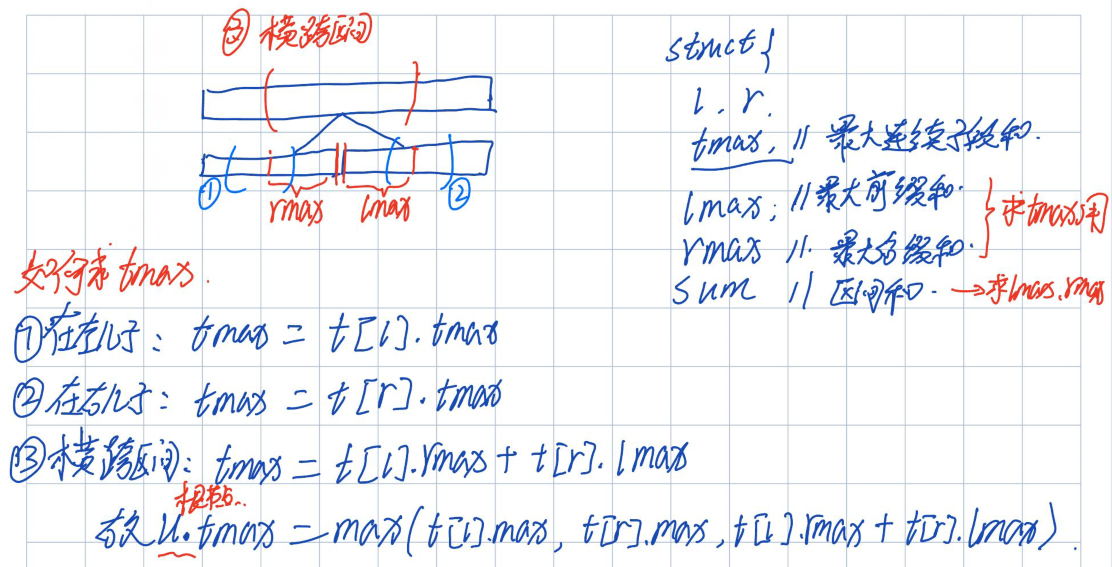
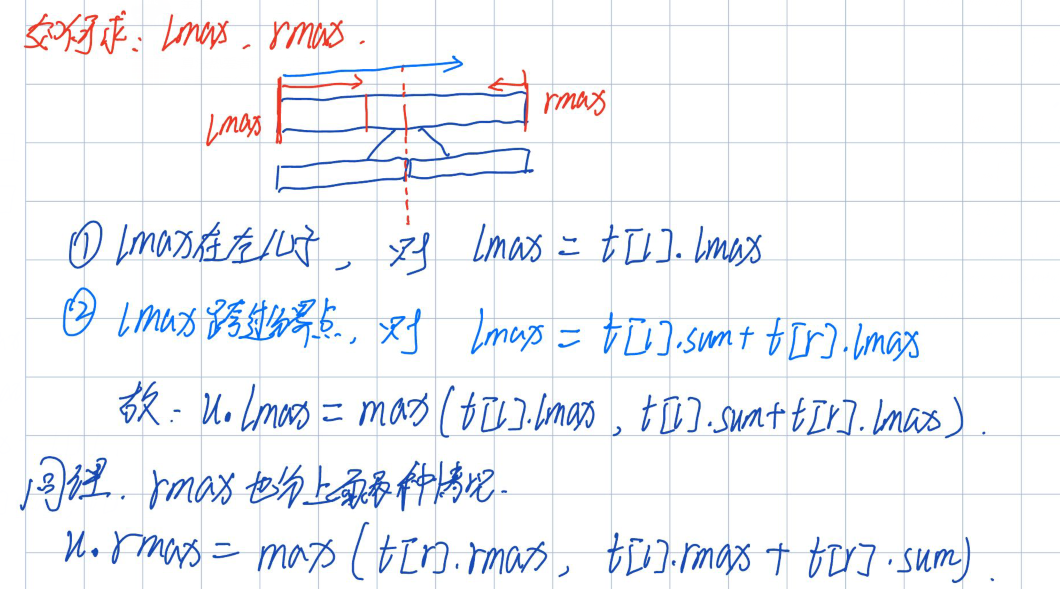
2. 想求tmax，用到了lmax,rmax，然后求得了tmax，那么如何求lmax,rmax，那么看下图；对于根节点来说，lmax分为两种情况：①从区间左端点开始，没越过分界线结束，那么根节点的lmax = 左儿子的lmax；②从区间左端点开始，越过分界线，那么根节点的lmax=左儿子的区间和（t[l].sum）+ 右儿子的最大前缀和（t[r].lmax）；所以根节点的lmax取值为上面两种情况的max值；
   同理rmax的求法一样，也是上面两种情况，可以得到下图的结论；

3. 上面求lmax,rmax用到的sum怎么求呢，直接由左儿子、右儿子的sum加起来就行；

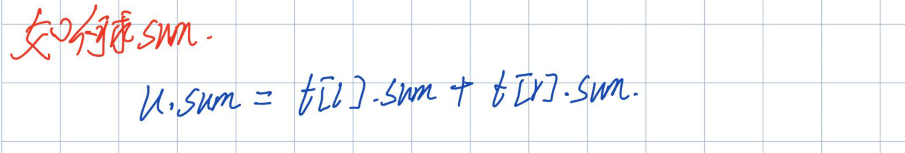
4. 那么通过上面3条对根节点的分析，可以求得tmax，那对于根的左儿子，他也算一个根，同样的做法来求，递归进行即可；
5. 这题由于有用于建立线段树的初始数组a，所以建树时候要注意初始化叶子结点，并且要pushup一下父节点，凡是修改了叶子结点,包括赋值，都要顺带给父亲更新一下；然后推荐一个大佬的讲解，讲的非常好：AcWing 245. 你能回答这些问题吗（线段树）

分析

#include <bits/stdc++.h>

using namespace std;

const int N = 500010;
struct node {
    int l, r;
    int tmax; //最大连续子段和
    int lmax; //最大前缀和（从区间左端点出发）
    int rmax; //最大后缀和（从区间右端点出发）
    int sum; //区间和
};
int n, m;
int a[N];
node t[4 * N];

void pushup(node &u, node &l, node &r) {
    //根据上面推导的结论求u的 tmax,lmax,rmax,sum
    u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.sum = l.sum + r.sum;
}

//儿子结点向上更新父亲结点
void pushup(int u) {
    pushup(t[u], t[u << 1], t[u << 1 | 1]);
}

void build(int u, int l, int r) {
    t[u].l = l, t[u].r = r;
    //到叶子结点了
    if (l == r) {
        //本题有用于建立线段树的初始数组a，所以这里需要赋个值，对于单一一个点，这几个值相等
        t[u].tmax = t[u].lmax = t[u].rmax = t[u].sum = a[l];
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    //本题有用于建立线段树的初始数组a，所以需要更新下父亲
    pushup(u);
}

void modify(int u, int x, int v) {
    //找到叶子结点
    if (t[u].l == t[u].r) {
        t[u].tmax = t[u].lmax = t[u].rmax = t[u].sum = v;
        return;
    }
    //找叶子结点
    int mid = t[u].l + t[u].r >> 1;
    if (x <= mid)
        modify(u << 1, x, v);
    else
        modify(u << 1 | 1, x, v);
    //更新父亲（凡是修改了叶子结点,包括赋值，都要顺带给父亲更新一下）
    pushup(u);
}

node query(int u, int l, int r) {
    //1. [l,r]完全包含 u 的左右区间
    if (l <= t[u].l && r >= t[u].r)
        return t[u];
    int mid = t[u].l + t[u].r >> 1;
    //2. [l,r]完全在u的左儿子
    if (r <= mid)
        return query(u << 1, l, r);
        //3. [l,r]完全在u的右孩子
    else if (l >= mid + 1)
        return query(u << 1 | 1, l, r);
        //4. [l,r]横跨分界线（左右两边都有）
    else {
        auto left = query(u << 1, l, r);
        auto right = query(u << 1 | 1, l, r);
        node res;
        //计算res的tmax
        pushup(res, left, right);
        return res;
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }
    build(1, 1, n);
    while (m--) {
        int k, x, y;
        cin >> k >> x >> y;
        if (k == 1) {
            if (x > y)
                swap(x, y);
            cout << query(1, x, y).tmax << endl;
        } else {
            modify(1, x, y);
        }
    }
    return 0;
}