张量[1]是向量和矩阵到 n 维的推广。了解它们如何相互作用是机器学习的基础。
简介
虽然张量看起来是复杂的对象,但它们可以理解为向量和矩阵的集合。理解向量和矩阵对于理解张量至关重要。
向量是元素的一维列表:
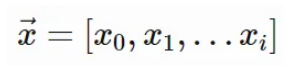
矩阵是向量的二维列表:
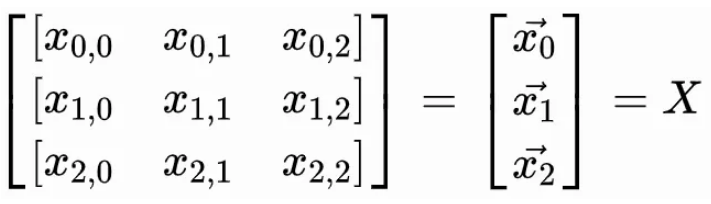
下标表示(行,列)。考虑矩阵的另一种方式是用向量作为元素的向量。请注意,它们通常用大写字母表示。
3D 张量可以被视为三维矩阵列表:

考虑 3D 张量的另一种方式是使用矩阵作为元素的向量。请注意,在本文中它们是用书法大写字母标注的。
4D 张量可以被认为是 3D 张量的四维列表:
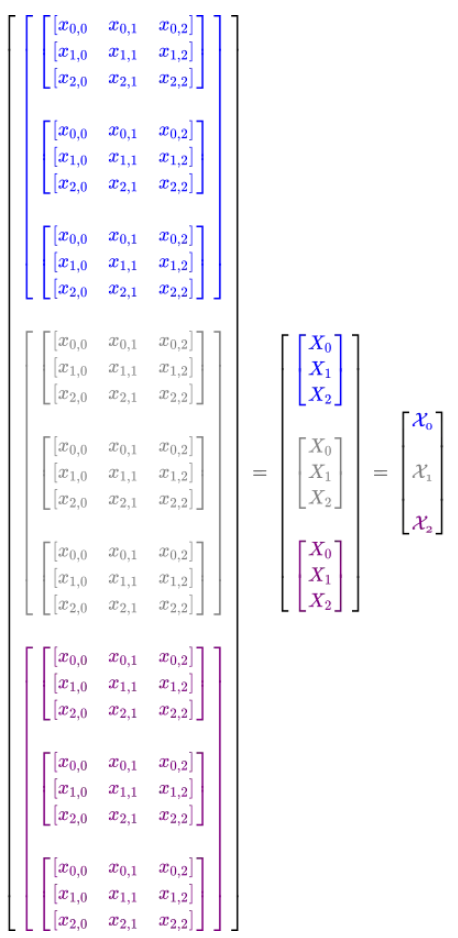
考虑 4D 张量的另一种方式是使用 3D 张量作为其元素的向量。这些可能会变得越来越复杂,但这是继续使用张量进行运算所必需的程度。
向量运算
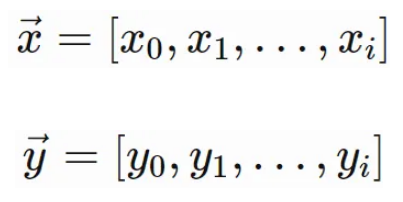
假设这些是相同长度的向量,i。接下来的操作主要是按元素进行的。这意味着每个向量中的相应元素被一起操作。
加法
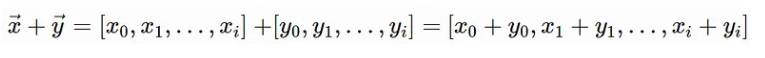
import torch
x = torch.tensor([1, 3, 5])
y = torch.tensor([3, 7, 4])
x + y
# tensor([ 4, 10, 9])
减法
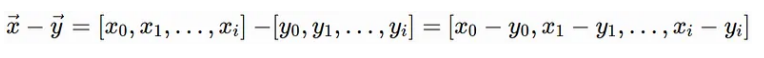
x = torch.tensor([1, 3, 5])
y = torch.tensor([3, 7, 4])
x - y
# tensor([-2, -4, 1])
点乘
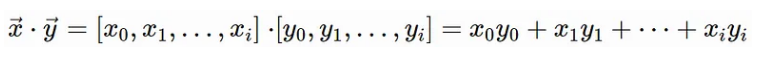
这也可以用求和来表示:
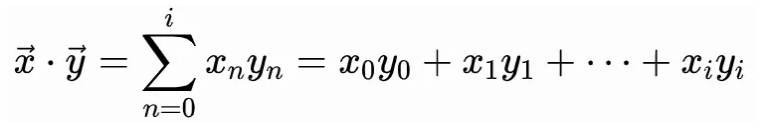
x = torch.tensor([1, 3, 5])
y = torch.tensor([3, 7, 4])
torch.dot(x, y) # 1*3 + 3*7 + 5*4 = 3 + 21 + 20 = 44
# tensor(44)
这也可以用 x @ y 来执行。点积的输出是一个标量。它不返回向量。
Hadamard(乘法)
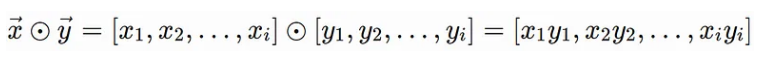
Hadamard 乘积用于执行逐元素乘法并返回一个向量。
x = torch.tensor([1, 3, 5])
y = torch.tensor([3, 7, 4])
x * y
# tensor([ 3, 21, 20])
标量乘法
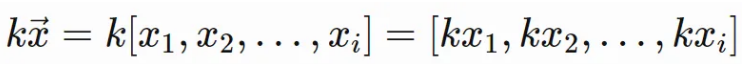
k 是标量,在大多数情况下是实数。
k = 5
x = torch.tensor([1, 3, 5])
k * x
# tensor([ 5, 15, 25])
由于 k 可以是分数,因此这也可以被视为标量除法。
矩阵乘法
请记住,矩阵是向量的集合。相同的操作适用于向量,但在涉及行和列时还有一些规则需要注意。
假设如下,其中 X 和 Y 的形状为 (4,3):
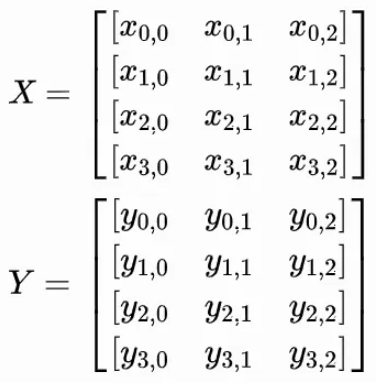
加法

X = torch.tensor([[1, 3, 5],
[3, 6, 1],
[6, 8, 5],
[7, 3, 2]])
Y = torch.tensor([[6, 3, 2],
[8, 5, 4],
[3, 1, 7],
[1, 8, 3]])
X + Y
# tensor([[ 7, 6, 7],
[11, 11, 5],
[ 9, 9, 12],
[ 8, 11, 5]])
减法

X = torch.tensor([[1, 3, 5],
[3, 6, 1],
[6, 8, 5],
[7, 3, 2]])
Y = torch.tensor([[6, 3, 2],
[8, 5, 4],
[3, 1, 7],
[1, 8, 3]])
X - Y
# tensor([[-5, 0, 3],
[-5, 1, -3],
[ 3, 7, -2],
[ 6, -5, -1]])
点积

在执行矩阵乘法时,重要的是要将矩阵视为由向量组成。通过这个视图,就可以清楚如何在矩阵上执行点积。发生乘法的唯一方法是第一个矩阵中的行数与第二个矩阵中的列数匹配。这导致:
-
(m, n) x (n, r) = (m, r)
如果情况并非如此,则必须转置其中一个矩阵以适应该顺序;这会切换行和列,但保留点积的向量。
在上图中,很明显,左侧矩阵中的每个向量(或行)都乘以第二个矩阵中的每个向量(或列)。因此,在此示例中,A 中的每个向量必须与 B 中的每个向量相乘,从而产生 16 个点积。
X = torch.tensor([[1, 3, 5],
[3, 6, 1],
[6, 8, 5],
[7, 3, 2]])
Y = torch.tensor([[6, 3, 2],
[8, 5, 4],
[3, 1, 7],
[1, 8, 3]])
X.matmul(Y.T) # X @ Y.T
# tensor([[ 25, 43, 41, 40],
[ 38, 58, 22, 54],
[ 70, 108, 61, 85],
[ 55, 79, 38, 37]])
Hadamard 积

Hadamard 乘积是逐元素乘法,因此其执行方式与加法和减法相同。
X = torch.tensor([[1, 3, 5],
[3, 6, 1],
[6, 8, 5],
[7, 3, 2]])
Y = torch.tensor([[6, 3, 2],
[8, 5, 4],
[3, 1, 7],
[1, 8, 3]])
X * Y
# tensor([[ 6, 9, 10],
[24, 30, 4],
[18, 8, 35],
[ 7, 24, 6]])
标量乘法

k = 5
X = torch.tensor([[1, 3, 5],
[3, 6, 1],
[6, 8, 5],
[7, 3, 2]])
k * X
# tensor([[ 5, 15, 25],
[15, 30, 5],
[30, 40, 25],
[35, 15, 10]])
三维张量运算
张量运算要求两个张量具有相同的大小,除非正在执行点积。
对于本节中的逐元素运算,假设两个张量的形状为 (3, 3, 2)。这意味着两个张量都包含三个 (3,2) 矩阵。如下所示:
import torch
gen = torch.Generator().manual_seed(2147483647)
X = torch.randint(0, 10, (3, 3, 2), generator=gen)
Y = torch.randint(0, 10, (3, 3, 2), generator=gen)
X = tensor([[[1, 4],
[9, 2],
[3, 0]],
[[4, 6],
[7, 7],
[1, 5]],
[[6, 8],
[1, 4],
[4, 9]]])
Y = tensor([[[8, 0],
[3, 6],
[6, 0]],
[[9, 1],
[0, 0],
[2, 2]],
[[7, 1],
[8, 1],
[9, 0]]])
加法
加法是按元素进行的,并且按预期执行。每个张量中对应的元素相互相加。
X + Y
tensor([[[ 9, 4],
[12, 8],
[ 9, 0]],
[[13, 7],
[ 7, 7],
[ 3, 7]],
[[13, 9],
[ 9, 5],
[13, 9]]])
减法
减法也是按元素进行的并且按预期执行。
X - Y
tensor([[[-7, 4],
[ 6, -4],
[-3, 0]],
[[-5, 5],
[ 7, 7],
[-1, 3]],
[[-1, 7],
[-7, 3],
[-5, 9]]])
点积

张量乘法比二维中的张量乘法稍微复杂一些。之前,矩阵乘法只有满足以下条件才能发生:
-
(m, n) x (n, r) = (m, r)
在三个维度上,这仍然是一个要求。但是,第一个轴必须相同:
-
(z, m, n) x (z, n, r) = (z, m, r)
为什么是这样?嗯,如前所述,二维的点积主要是将向量彼此相乘。在三维中,重点是按矩阵相乘,然后对这些矩阵中的每个向量执行点积。
上图应该有助于解释这一点。将两个 3D 张量视为矩阵向量可能会有所帮助。由于点积是通过按元素相乘然后求和来执行的,因此首先发生的事情是每个矩阵与其相应的矩阵相乘。当这种情况发生时,矩阵乘法会导致矩阵中的每个向量与其他向量执行点积。从某种意义上说,它就像一个嵌套的点积。
为了使 和 彼此相乘,必须调换 的第二轴和第三轴。并且两者的大小均为 (3, 3, 2)。这意味着必须变成(3,2,3)。这可以使用 Y.permute(0, 2, 1) 来完成,它转置第二和第三轴。或者,可以使用 Y.transpose(1,2)。
print(Y.transpose(1,2))
print(Y.transpose(1,2).shape) # Y.permute(0, 2, 1)
tensor([[[8, 3, 6],
[0, 6, 0]],
[[9, 0, 2],
[1, 0, 2]],
[[7, 8, 9],
[1, 1, 0]]])
torch.Size([3, 2, 3])
通过适当的调整大小,现在可以使用 matmul 或 @ 执行张量乘法。输出的形状应为 (3, 3, 2) x (3, 2, 3) = (3, 3, 3)。
X.matmul(Y.transpose(1,2)) # X @ Y.transpose(1,2)
tensor([[[ 8, 27, 6],
[72, 39, 54],
[24, 9, 18]],
[[42, 0, 20],
[70, 0, 28],
[14, 0, 12]],
[[50, 56, 54],
[11, 12, 9],
[37, 41, 36]]])
Hadamard 积
Hadamard 积的性能符合预期,并在 3D 张量的矩阵中按元素相乘。
X * Y
tensor([[[ 8, 0],
[27, 12],
[18, 0]],
[[36, 6],
[ 0, 0],
[ 2, 10]],
[[42, 8],
[ 8, 4],
[36, 0]]])
标量乘法
标量乘法也按预期执行。
k = 5
k*X
tensor([[[ 5, 20],
[45, 10],
[15, 0]],
[[20, 30],
[35, 35],
[ 5, 25]],
[[30, 40],
[ 5, 20],
[20, 45]]])
四维张量运算
四维张量运算仍然要求两个张量具有相同的大小。
对于本部分,假设形状为 (2, 3, 3, 2)。这意味着两个 4D 张量都包含两个 3D 张量,并且每个张量都包含三个 (3,2) 矩阵。如下所示:
import torch
gen = torch.Generator().manual_seed(2147483647)
X = torch.randint(0, 10, (2, 3, 3, 2), generator=gen)
Y = torch.randint(0, 10, (2, 3, 3, 2), generator=gen)
X
# 4d tensor
tensor([
# 3d tensor
[
# matrix 1
[[1, 4],
[9, 2],
[3, 0]],
# matrix 2
[[4, 6],
[7, 7],
[1, 5]],
# matrix 3
[[6, 8],
[1, 4],
[4, 9]]],
# 3d tensor
[
# matrix 1
[[8, 0],
[3, 6],
[6, 0]],
# matrix 2
[[9, 1],
[0, 0],
[2, 2]],
# matrix 3
[[7, 1],
[8, 1],
[9, 0]]]])
Y
# 4d tensor
tensor([
# 3d tensor
[
# matrix 1
[[6, 3],
[6, 4],
[5, 7]],
# matrix 2
[[3, 7],
[2, 0],
[5, 1]],
# matrix 3
[[0, 4],
[0, 8],
[0, 6]]],
# 3d tensor
[
# matrix 1
[[0, 5],
[8, 6],
[1, 0]],
# matrix 2
[[5, 1],
[1, 6],
[1, 2]],
# matrix 3
[[6, 0],
[2, 6],
[1, 5]]]])
加法
加法、减法和哈达玛积仍然按预期按元素执行。
X + Y
tensor([[[[ 7, 7],
[15, 6],
[ 8, 7]],
[[ 7, 13],
[ 9, 7],
[ 6, 6]],
[[ 6, 12],
[ 1, 12],
[ 4, 15]]],
[[[ 8, 5],
[11, 12],
[ 7, 0]],
[[14, 2],
[ 1, 6],
[ 3, 4]],
[[13, 1],
[10, 7],
[10, 5]]]])
减法
X - Y
tensor([[[[-5, 1],
[ 3, -2],
[-2, -7]],
[[ 1, -1],
[ 5, 7],
[-4, 4]],
[[ 6, 4],
[ 1, -4],
[ 4, 3]]],
[[[ 8, -5],
[-5, 0],
[ 5, 0]],
[[ 4, 0],
[-1, -6],
[ 1, 0]],
[[ 1, 1],
[ 6, -5],
[ 8, -5]]]])
点积

在四维中,张量乘法将具有与三维和二维中相同的要求。它还需要第一轴和第二轴与两个张量匹配:
-
(c、z、m、n) x (c、z、n、r) = (c、z、m、r)
在三维空间中,进行矩阵乘法,然后进行向量之间的点积。相同的步骤将在四个维度中发生,但首先将每个 3D 张量与其相应的 3D 张量相乘。然后,它们的每个矩阵将相互相乘。最后,它们的向量将相互执行点积。这可以在上图中看到。
对于本例, 和 的大小为 (2, 3, 3, 2)。为了进行乘法运算,必须调换 的第三轴和第四轴。这可以按照与之前使用 Y.permute(0, 1, 3, 2) 或 Y.transpose(2,3) 相同的方式完成。转置后的形状为 (2, 3, 2, 3)。
结果的形状应为 (2, 3, 3, 2) x (2, 3, 2, 3) = (2,3,3,3)。这意味着将有两个 3D 张量,每个张量将包含三个 (3,3) 矩阵。这个结果可以使用 matmul 或 @ 获得。
X.matmul(Y.transpose(2,3)) # X @ Y.transpose(2,3)
tensor([[[[18, 22, 33],
[60, 62, 59],
[18, 18, 15]],
[[54, 8, 26],
[70, 14, 42],
[38, 2, 10]],
[[32, 64, 48],
[16, 32, 24],
[36, 72, 54]]],
[[[ 0, 64, 8],
[30, 60, 3],
[ 0, 48, 6]],
[[46, 15, 11],
[ 0, 0, 0],
[12, 14, 6]],
[[42, 20, 12],
[48, 22, 13],
[54, 18, 9]]]])
Hadamard 积
X * Y
tensor([[[[ 6, 12],
[54, 8],
[15, 0]],
[[12, 42],
[14, 0],
[ 5, 5]],
[[ 0, 32],
[ 0, 32],
[ 0, 54]]],
[[[ 0, 0],
[24, 36],
[ 6, 0]],
[[45, 1],
[ 0, 0],
[ 2, 4]],
[[42, 0],
[16, 6],
[ 9, 0]]]])
标量乘法
k = 5
k * X
tensor([[[[ 5, 20],
[45, 10],
[15, 0]],
[[20, 30],
[35, 35],
[ 5, 25]],
[[30, 40],
[ 5, 20],
[20, 45]]],
[[[40, 0],
[15, 30],
[30, 0]],
[[45, 5],
[ 0, 0],
[10, 10]],
[[35, 5],
[40, 5],
[45, 0]]]])
Reference
Source: https://medium.com/@hunter-j-phillips/a-simple-introduction-to-tensors-c4a8321efffc
本文由 mdnice 多平台发布




![[SQL开发笔记]LIKE操作符:在 WHERE 子句中搜索列中的指定模式](https://img-blog.csdnimg.cn/0e3e4b0e5dc7424da8e210b34a594116.png)




![buuctf_练[GYCTF2020]FlaskApp](https://img-blog.csdnimg.cn/img_convert/16756c3a126348e1e74c0cd16fa55e0f.png)