CTF-Crypto学习记录-第三天 MD5加密算法（信息摘要算法）“ “

news2024/10/7 18:22:11

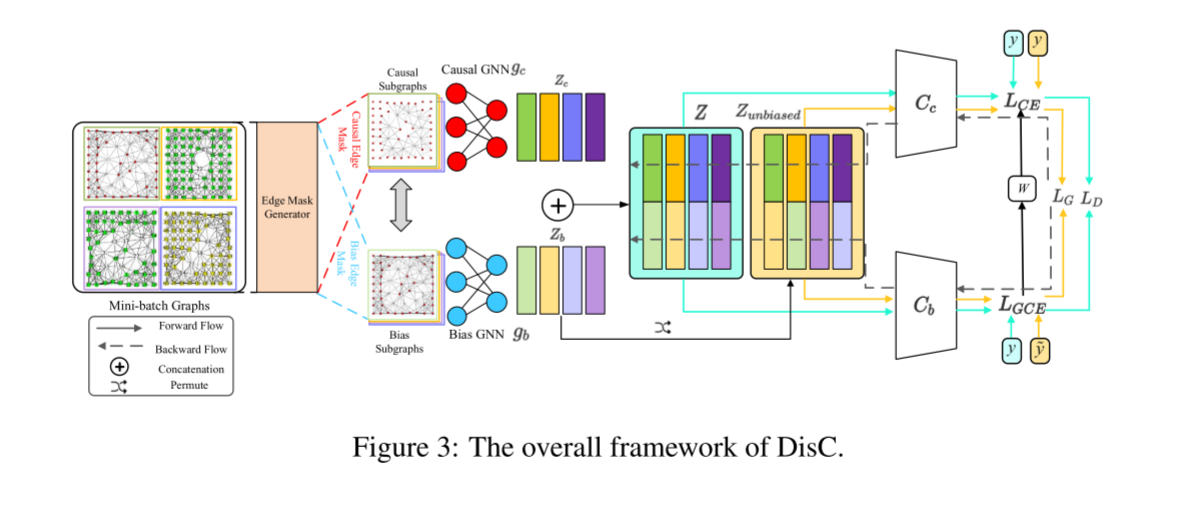
文章目录

0x1 MD5 基本介绍
0x2 MD5 加密特点
0x3 MD5 加密原理步骤
- 0x01 对明文数据进行信息填充
- 0x02 设置初始变量
- 0x03 加密运算过程
- - 加密运算流程图：
  - 四个非线性函数：
  - Mj表示消息的第j个子分组（从0到15），<<：
  - 四轮运算：
- MD5 伪代码

0x1 MD5 基本介绍

MD5加密算法，也称信息摘要算法（Message-Digest Algorith 5），所谓的信息摘要就是将明文内容按一定的规则生成一段哈希（Hash）值，即得到这段明文内容的消息摘要。
利用MD5可以基于任意长度的明文字符串生成128-bit的哈希值，结果唯一且不可逆。

0x2 MD5 加密特点

1.压缩性：任意长度的数据，算出的MD5值长度都是固定的
2.高效性：MD5的计算过程很快速
3.雪崩效应：对原数据进行修改，哪怕只修改一个字节，对MD5值都是巨大的改变
4.强抗碰撞性：极难找到不同的俩个明文数据，拥有相同的MD5值。
5.不可逆性：无法从MD5值逆向得到明文数据

MD5的不可逆性来源于他是一种散列函数，使用hash算法，在计算过程中原文的部分信息是有丢失的。

0x3 MD5 加密原理步骤

MD5算法流程图：
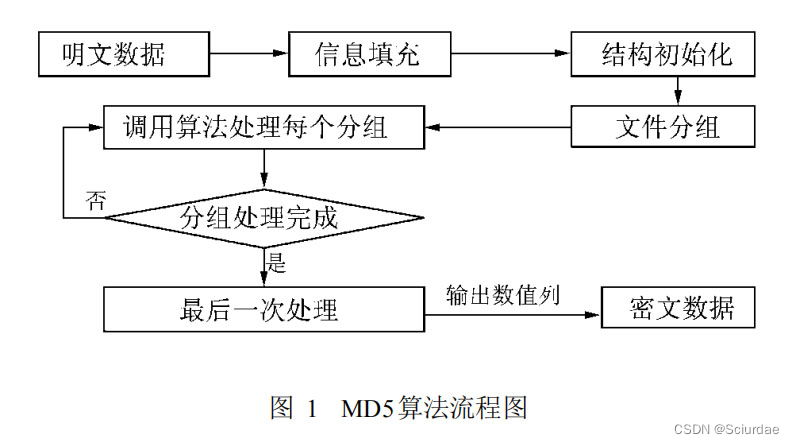
在这里插入图片描述

0x01 对明文数据进行信息填充

对原始信息进行填充，填充之后，要求信息的长度对512求余等于448。
填充的第一步有俩种情况：

原始信息长度取余不是448，假设原始信息长度为b bit，那么在信息的b+1 bit 处填充1，剩余的位填充0，直到信息长度对512取余正好等于448。
原始信息长度取余正好等于448，在这个时候我们要填充512 bit的信息长度，也就是直到信息长度对512取余再次等于448；

所以填充的最少位数是 1 ，最大位数是 512；

第二步，填充信息长度，我们需要把原始信息转换成 bit 为单位，在第一步取余后结果是 448 ，这个时候我们需要再填充 64 bit 的长度信息，使整个信息恰好可以被 512 整除，从这里也可以看出，计算MD5时，是将信息分成若干个分组进行处理的，每个分组信息长度为512 bit。

0x02 设置初始变量

MD5中有四个32位被称作链接变量（Chaining Variable）的整数参数，他们分别是：

A=0x01234567，
B=0x89abcdef，
C=0xfedcba98，
D=0x76543210，

如果是在程序中进行存储；
在这里插入图片描述

0x03 加密运算过程

加密运算流程图：

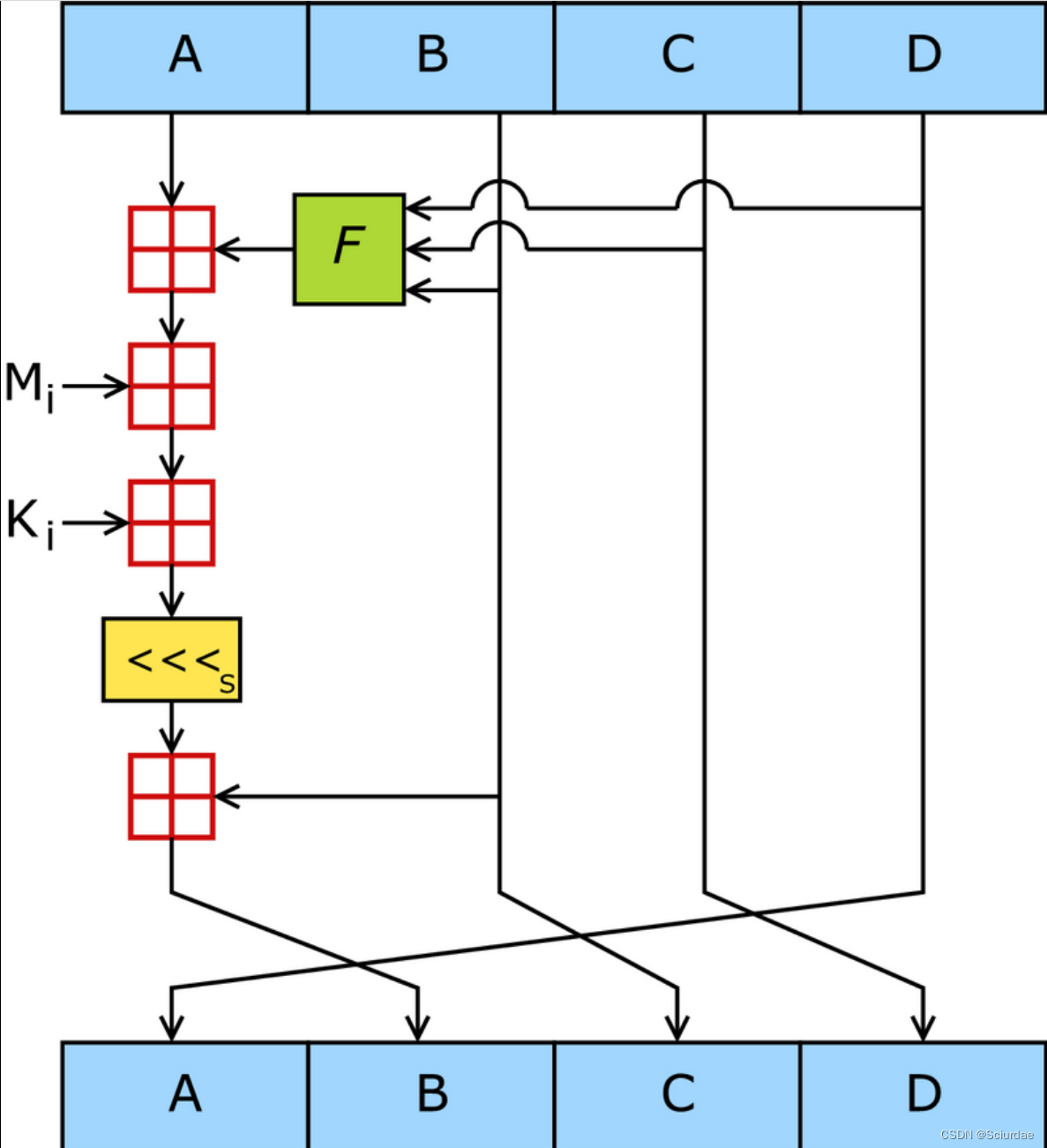
在这里插入图片描述
第一分组需要将上面四个链接变量复制到另外四个变量中：A到A，B到B，C到C，D到D。从第二分组开始的变量为上一分组的运算结果。

一个MD5运算— 由类似的64次循环构成，分成4组16次。F 一个非线性函数；一个函数运算一次。Mi 表示一个 32-bits 的输入数据，Ki 表示一个 32-bits 常数，用来完成每次不同的计算。

主循环有四轮（上面提到的64次循环，4组16次），每轮循环都很相似。第一轮进行16次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算，然后将所得结果加上第四个变量，文本的一个子分组和一个常数。再将所得结果向左环移一个不定的数，并加上****a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。

四个非线性函数：

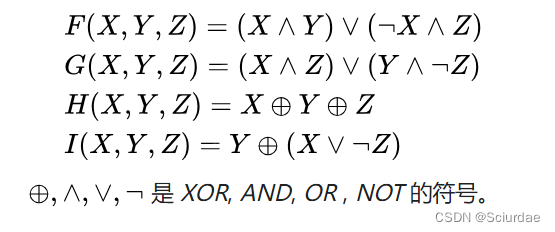
在这里插入图片描述

Mj表示消息的第j个子分组（从0到15），<<：

FF(a,b,c,d,Mj,s,ti)表示a=b+((a+F(b,c,d)+Mj+ti)<<<s)
GG(a,b,c,d,Mj,s,ti)表示a=b+((a+G(b,c,d)+Mj+ti)<<<s)
HH(a,b,c,d,Mj,s,ti)表示a=b+((a+H(b,c,d)+Mj+ti)<<<s)
II(a,b,c,d,Mj,s,ti)表示a=b+((a+I(b,c,d)+Mj+ti)<<<s)

四轮运算：

 第一轮
a=FF(a,b,c,d,M0,7,0xd76aa478)
b=FF(d,a,b,c,M1,12,0xe8c7b756)
c=FF(c,d,a,b,M2,17,0x242070db)
d=FF(b,c,d,a,M3,22,0xc1bdceee)
a=FF(a,b,c,d,M4,7,0xf57c0faf)
b=FF(d,a,b,c,M5,12,0x4787c62a)
c=FF(c,d,a,b,M6,17,0xa8304613)
d=FF(b,c,d,a,M7,22,0xfd469501)
a=FF(a,b,c,d,M8,7,0x698098d8)
b=FF(d,a,b,c,M9,12,0x8b44f7af)
c=FF(c,d,a,b,M10,17,0xffff5bb1)
d=FF(b,c,d,a,M11,22,0x895cd7be)
a=FF(a,b,c,d,M12,7,0x6b901122)
b=FF(d,a,b,c,M13,12,0xfd987193)
c=FF(c,d,a,b,M14,17,0xa679438e)
d=FF(b,c,d,a,M15,22,0x49b40821)

第二轮
a=GG(a,b,c,d,M1,5,0xf61e2562)
b=GG(d,a,b,c,M6,9,0xc040b340)
c=GG(c,d,a,b,M11,14,0x265e5a51)
d=GG(b,c,d,a,M0,20,0xe9b6c7aa)
a=GG(a,b,c,d,M5,5,0xd62f105d)
b=GG(d,a,b,c,M10,9,0x02441453)
c=GG(c,d,a,b,M15,14,0xd8a1e681)
d=GG(b,c,d,a,M4,20,0xe7d3fbc8)
a=GG(a,b,c,d,M9,5,0x21e1cde6)
b=GG(d,a,b,c,M14,9,0xc33707d6)
c=GG(c,d,a,b,M3,14,0xf4d50d87)
d=GG(b,c,d,a,M8,20,0x455a14ed)
a=GG(a,b,c,d,M13,5,0xa9e3e905)
b=GG(d,a,b,c,M2,9,0xfcefa3f8)
c=GG(c,d,a,b,M7,14,0x676f02d9)
d=GG(b,c,d,a,M12,20,0x8d2a4c8a)

第三轮
a=HH(a,b,c,d,M5,4,0xfffa3942)
b=HH(d,a,b,c,M8,11,0x8771f681)
c=HH(c,d,a,b,M11,16,0x6d9d6122)
d=HH(b,c,d,a,M14,23,0xfde5380c)
a=HH(a,b,c,d,M1,4,0xa4beea44)
b=HH(d,a,b,c,M4,11,0x4bdecfa9)
c=HH(c,d,a,b,M7,16,0xf6bb4b60)
d=HH(b,c,d,a,M10,23,0xbebfbc70)
a=HH(a,b,c,d,M13,4,0x289b7ec6)
b=HH(d,a,b,c,M0,11,0xeaa127fa)
c=HH(c,d,a,b,M3,16,0xd4ef3085)
d=HH(b,c,d,a,M6,23,0x04881d05)
a=HH(a,b,c,d,M9,4,0xd9d4d039)
b=HH(d,a,b,c,M12,11,0xe6db99e5)
c=HH(c,d,a,b,M15,16,0x1fa27cf8)
d=HH(b,c,d,a,M2,23,0xc4ac5665)

第四轮
a=II(a,b,c,d,M0,6,0xf4292244)
b=II(d,a,b,c,M7,10,0x432aff97)
c=II(c,d,a,b,M14,15,0xab9423a7)
d=II(b,c,d,a,M5,21,0xfc93a039)
a=II(a,b,c,d,M12,6,0x655b59c3)
b=II(d,a,b,c,M3,10,0x8f0ccc92)
c=II(c,d,a,b,M10,15,0xffeff47d)
d=II(b,c,d,a,M1,21,0x85845dd1)
a=II(a,b,c,d,M8,6,0x6fa87e4f)
b=II(d,a,b,c,M15,10,0xfe2ce6e0)
c=II(c,d,a,b,M6,15,0xa3014314)
d=II(b,c,d,a,M13,21,0x4e0811a1)
a=II(a,b,c,d,M4,6,0xf7537e82)
b=II(d,a,b,c,M11,10,0xbd3af235)
c=II(c,d,a,b,M2,15,0x2ad7d2bb)
d=II(b,c,d,a,M9,21,0xeb86d391)

MD5 伪代码

//Note: All variables are unsigned 32 bits and wrap modulo 2^32 when calculating
var int[64] r, k

//r specifies the per-round shift amounts
r[ 0..15]：= {7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22} 
r[16..31]：= {5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20}
r[32..47]：= {4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23}
r[48..63]：= {6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21}

//Use binary integer part of the sines of integers as constants:
for i from 0 to 63
    k[i] := floor(abs(sin(i + 1)) × 2^32)

//Initialize variables:
var int h0 := 0x67452301
var int h1 := 0xEFCDAB89
var int h2 := 0x98BADCFE
var int h3 := 0x10325476

//Pre-processing:
append "1" bit to message
append "0" bits until message length in bits ≡ 448 (mod 512)
append bit length of message as 64-bit little-endian integer to message

//Process the message in successive 512-bit chunks:
for each 512-bit chunk of message
    break chunk into sixteen 32-bit little-endian words w[i], 0 ≤ i ≤ 15

    //Initialize hash value for this chunk:
    var int a := h0
    var int b := h1
    var int c := h2
    var int d := h3

    //Main loop:
    for i from 0 to 63
        if 0 ≤ i ≤ 15 then
            f := (b and c) or ((not b) and d)
            g := i
        else if 16 ≤ i ≤ 31
            f := (d and b) or ((not d) and c)
            g := (5×i + 1) mod 16
        else if 32 ≤ i ≤ 47
            f := b xor c xor d
            g := (3×i + 5) mod 16
        else if 48 ≤ i ≤ 63
            f := c xor (b or (not d))
            g := (7×i) mod 16
 
        temp := d
        d := c
        c := b
        b := leftrotate((a + f + k[i] + w[g]),r[i]) + b
        a := temp
    Next i
    //Add this chunk's hash to result so far:
    h0 := h0 + a
    h1 := h1 + b 
    h2 := h2 + c
    h3 := h3 + d
End ForEach
var int digest := h0 append h1 append h2 append h3 //(expressed as little-endian)