• 前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化。

我们通过一个例子来理解前缀和算法的优势：

一维前缀和：

www.nowcoder.com

我们可以通过暴力的解法去解决这个问题，但是这样时间复杂度会比较高，达到O（n*q）

我们可以对暴力解法进行优化：

我们以【1,4,7,2,5,8,3,6,9】这个数组来讲解前缀和（快速求出数组中某个连续区间的元素和）这个算法

index为数组下标，至于为什么下标从一开始后面会讲！！！

我们提前弄一个前缀和数组dp，这个数组的元素dp【i】代表【1，i】区间内所有元素之和

我们在求dp的时候肯定不可以用暴力解法，不然的话时间复杂度又上去了，

dp【i】代表 【1，i】区间内所有元素之和，那dp【i-1】代表 【1，i-1】区间内所有元素之和

• dp【i】就可以等于dp【i-1】+arr【i】

那我们再来看看题目，题目要求我们输出从l到r区间内所有元素之和

那我们可以直接输出dp【r】-dp【l-1】

#include <iostream>
#include<vector>
using namespace std;
int main() {
    int n,q;
    cin>>n>>q;
    vector<int> arr(n+1);
    for(int i=1;i<=n;i++) cin>>arr[i];
    vector<long long> dp(n+1);
    for(int i=1;i<=n;i++) dp[i]=dp[i-1]+arr[i];
    while(q--)
    {
        int l,r;
        cin>>l>>r;
        cout<<dp[r]-dp[l-1]<<endl;
    }
    return 0;
}
// 64 位输出请用 printf("%lld")

二位前缀和：

首先如果我们使用暴力解法时间复杂度，直接就是O(nmq），我们可以对其使用前缀和算法优化

我们可以创建一个（n+1）（m+1）的的数组arr和（n+1）（m+1）的的前缀和数组dp

• 这里数组坐标加一也是为了防止越界的情况

dp【i】【j】代表从（1,1）~（i，j）这个区间内所有元素之和

我们如何快速求出dp【i】【j】的值呢？以下面这个数组为例，假设我们要求的是dp【3】【3】

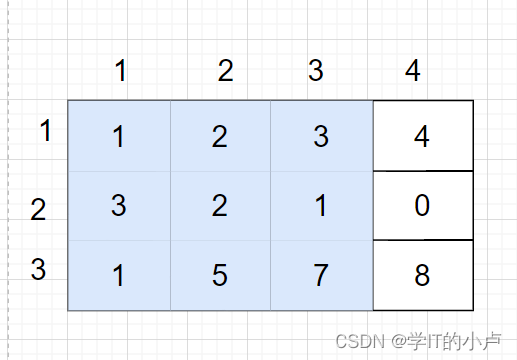
我们先来观察一个通用图：我们要求多少A+B+C+D之和

A+B+C+D=（A+B）+（A+C）+D-A，括号内的是一个整体

我们可以结合下标的关系推导进一步的关系

A+B+C+D=（A+B）+（A+C）+D-A

​ =dp【i-1】【j】+dp【i】【j-1】+arr【i】【j】-dp【i-1】【j-1】

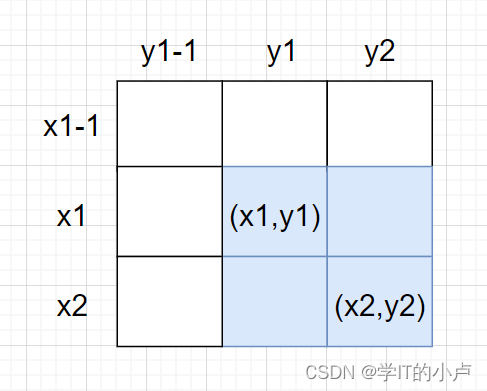
这样我们就求出来了dp的每一个数了，回到题目上，题目要求我们输出（x1,y1)~(x2,y2)这个区间内的所有元素之和，假设让我们输出是是这个区间

编辑

• D=（A+B+C+D）-（A+B）-（A+C）+A

编辑

D=（A+B+C+D）-（A+B）-（A+C）+A

= dp【x2】【y2】-dp【x1-1】【y2】-dp【x2】【y1-1】+dp【x1-1】【y1-1】

为了防止越界，我们开辟数组也要多开一行一列