从听到傅立叶变换这个名词后到现在已经四年了，这次终于对傅立叶变换有了一个基本的初步了解。记录一下，这个傅立叶变换也同时记录了我本科到研究生的四年，一路以来跌跌撞撞，没想到最后还是入了图像的坑

数字图像处理——傅立叶变换

欧拉公式

对于一个复平面（对于欧几里得平面而言，把实数作为x轴，虚数作为y轴）

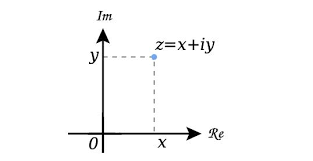
若在复平面上存在一个单位圆，所以在单位圆上的点可以表示为$\cos \theta +\sin \theta \cdot i$

对于泰勒公式：
$$\begin{array}{rl}{e}^x& =1+x+\frac{1}{2}{x}^2+\frac{1}{6}{x}^3+\cdots +\frac{1}{n!}{x}^n=\sum _{i=0}^n\frac{1}{i!}{x}^i\\ \sin x& =x-\frac{1}{6}{x}^3+\frac{1}{120}{x}^5+\cdots +\frac{(-1{)}^{2k-1}}{(2k-1)!}{x}^{2k-1}=\sum _{i=1}^n\frac{(-1{)}^{i-1}}{(2i-1)!}{x}^{2i-1}\\ \cos x& =1-\frac{1}{2}{x}^2+\frac{1}{24}{x}^4+\cdots +\frac{(-1{)}^k}{(2k)!}{x}^{2k}=\sum _{i=0}^n\frac{(-1{)}^i}{(2i)!}{x}^{2i}\end{array}$$
令$x=\theta i$，则可得$e^{\theta i}=\cos \theta +\sin \theta \cdot i$

则单位圆存在如下表示：

傅立叶级数

对于傅立叶级数表示如果存在周期为$T$的函数，那它一定可以由一组正弦和余弦函数表示，即：
$$f(x)=a_0+\sum _{n=1}^{\infty }(a_n\sin \frac{2\pi n}{T}x+b_n\cos \frac{2\pi n}{T}x)$$
同时因为欧拉公式$e^{\theta i}=\cos \theta +\sin \theta \cdot i$，所以
$$\{\begin{array}{l}{e}^{\theta i}=\cos \theta +\sin \theta \cdot i\\ e^{-\theta i}=\cos \theta -\sin \theta \cdot i\end{array}\Rightarrow \{\begin{array}{l}\cos \theta =\frac{e^{\theta i}+e^{-\theta i}}{2}\\ \sin \theta =\frac{e^{\theta i}-e^{-\theta i}}{2i}\end{array}$$
带入傅立叶级数可得：
$$\begin{array}{rl}f(x)& =a_0+\sum _{n=1}^{\infty }(a_n\frac{e^{\frac{2\pi n}{T}x\cdot i}+e^{-\frac{2\pi n}{T}x\cdot i}}{2}+b_n\frac{e^{\frac{2\pi n}{T}x\cdot i}-e^{-\frac{2\pi n}{T}x\cdot i}}{2i})\\ & =a_0+\sum _{n=1}^{\infty }(a_n\frac{e^{\frac{2\pi n}{T}x\cdot i}+e^{-\frac{2\pi n}{T}x\cdot i}}{2}-b_n\frac{e^{\frac{2\pi n}{T}x\cdot i}-e^{-\frac{2\pi n}{T}x\cdot i}}{2}\cdot i)\\ & =a_0+\sum _{n=0}^{\infty }(\frac{a_n-b_n\cdot i}{2}{e}^{\frac{2\pi n}{T}x\cdot i}+\frac{a_n+b_n\cdot i}{2}{e}^{-\frac{2\pi n}{T}x\cdot i})\end{array}$$
令$c_0=a_0,c_n=\frac{a_n-b_n\cdot i}{2},c_{-n}=\frac{a_n+b_n\cdot i}{2}$，则
$$f(x)=\sum _{n=-\infty }{c}_n{e}^{\frac{2\pi n}{T}x\cdot i}$$
其中$c_n$为傅立叶级数的系数，它代表原始函数$f(x)$在特定频率$n$处的强度

对于$f(x)$，此时等号左右两侧同时乘上$e^{-\frac{2\pi n}{T}x\cdot i}$，则
$$e^{-\frac{2\pi n}{T}x\cdot i}\times f(x)=e^{-\frac{2\pi n}{T}x\cdot i}\times \sum _{n=-\infty }{c}_n{e}^{\frac{2\pi n}{T}x\cdot i}$$
在一个周期$T$内进行积分:
$$\begin{array}{rl}{\int }_0^{T}f(x)e^{-\frac{2\pi n}{T}x\cdot i}dx& ={\int }_0^T{e}^{-\frac{2\pi n}{T}x\cdot i}\times \sum _{n=-\infty }{c}_n{e}^{\frac{2\pi n}{T}x\cdot i}dx\\ & ={\int }_0^T\sum _{n=-\infty }{c}_n{e}^{\frac{2\pi n^{\prime }}{T}x\cdot i}dx\end{array}$$
对于$e^{\frac{2\pi n^{\prime }}{T}x\cdot i}$在一个周期内积分，即考虑$e^{\frac{2\pi (n-m)}{T}x\cdot i}$在一个周期上积分

当$n=m$时，$e^{\frac{2\pi (n-m)}{T}x\cdot i}=e^0=1$，此时
$${\int }_0^T{e}^{\frac{2\pi n^{\prime }}{T}x\cdot i}dx=T$$
当$n\ne m$时，$e^{\frac{2\pi n^{\prime }}{T}x\cdot i}=\cos \frac{2\pi n^{\prime }}{T}x+\sin \frac{2\pi n^{\prime }}{T}x\cdot i$，此时
$$\begin{array}{rl}{\int }_0^T{e}^{\frac{2\pi n^{\prime }}{T}x\cdot i}dx& ={\int }_0^T(\cos \frac{2\pi n^{\prime }}{T}x+\sin \frac{2\pi n^{\prime }}{T}x\cdot i)dx\\ & ={\int }_0^T\cos \frac{2\pi n^{\prime }}{T}xdx+i{\int }_0^T\sin \frac{2\pi n^{\prime }}{T}xdx\\ & =0\end{array}$$
所以：
$$\begin{array}{rl}{\int }_0^{T}f(x)e^{-\frac{2\pi n}{T}x\cdot i}dx& ={\int }_0^T{e}^{-\frac{2\pi n}{T}x\cdot i}\times \sum _{n=-\infty }{c}_n{e}^{\frac{2\pi n}{T}x\cdot i}dx\\ & ={\int }_0^T\sum _{n=-\infty }{c}_n{e}^{\frac{2\pi n^{\prime }}{T}x\cdot i}dx\\ & =c_{n}T,n=n^{\prime }\end{array}$$
可得
$$c_n=\frac{1}{T}{\int }_0^{T}f(x)e^{-\frac{2\pi n}{T}x\cdot i}dx$$
对于三角函数$A\sin (\omega x+\phi )$中周期为$T=\frac{2\pi }{\omega }$，相位为$\phi$，振幅为$A$，频率为$\Delta f=\frac{1}{T}$。

在复平面中
$$c_n\times e^{\frac{2\pi n}{T}x\cdot i}=c_n\times (\cos \frac{2\pi n}{T}x+\sin \frac{2\pi n}{T}x\cdot i)$$
所以频率为$\Delta f=\frac{T}{2\pi n}$，振幅为$c_n$。

傅立叶变换

连续型

当周期$T$趋向于无穷大时，函数不再是周期的，而是在整个实数轴上定义。此时频率$\Delta f=\frac{1}{T}\to 0$，这意味着频率变得连续，而不再是离散的。当$T\to \infty$时，$\omega =\frac{2\pi n}{T}$，则可以将$n\Delta f$替换为一个连续的频率。于是，我们从傅立叶级数系数 $c_n$ 得到傅立叶变换：
$$\{\begin{array}{l}{c}_n=\frac{1}{T}{\int }_0^{T}f(x)e^{-\frac{2\pi n}{T}x\cdot i}dx\\ T=\infty \end{array}\Rightarrow F(\omega )=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }f(x)e^{-\omega x\cdot i}dx,\omega =\frac{2\pi n}{T}$$

离散型

已知连续型的傅立叶变换为$F(\omega )=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }f(x)e^{-\omega x\cdot i}dx$

当我们考虑离散的信号时，而不是连续的信号，我们需要使用离散傅立叶变换(Discrete Fourier Transform, DFT)。给定一个离散信号序列 $x[n]$，其DFT为 $X[k]$，定义如下：

$$X[k]=\sum _{n=0}^{N-1}x[n]\cdot e^{-j\frac{2\pi kn}{N}}$$
其中:

• $x[n]$ 是在时域中的离散信号。
• $X[k]$ 是在频域中的离散频率响应。
• $N$ 是信号的总长度或总样本数。
• $k$ 是离散频率的索引，范围从 $0$ 到 $N-1$。