- 121. 买卖股票的最佳时机
- 122.买卖股票的最佳时机II
第一题:买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
-
示例 1:
-
输入:[7,1,5,3,6,4]
-
输出:5
0、贪心的算法思路是求得局部最优,然后求得全局最优,
1、动态规划的思路是用一个二维dp数组,一维dp[i][0]表示第i天持有股票所得最多现金
另一维dp[i][1]表示第i天不持有股票所得最多现金。
(1)确定dp数组及其下标含义
dp[i][0]: 表示第i天持有股票所得最多现金,可正可负
dp[i][1]: 表示第i天不持有股票所得最多现金
(2)确定递推公式
首先dp[i][0]可以由两个状态求出来
要么是今天没买,保持昨天的状态,也就是dp[i-1][0]
要么是今天买了,所得现金就是买入今天股票后所得现金即:-prices[i]
所以dp[i][0]=max(dp[i-1][0],-prices[i]);
对于dp[i][1]也可以由两个状态求出来
要么是前一天就卖出去了,今天就维持现状,所持现金就没变:dp[i-1][1]
要么是今天正好卖出,所得现金就是今天的价格卖出的所得现金:prices[i]+dp[i-1][0]
同样dp[i][1]取最大的,dp[i][1]=max(dp[i-1][1],prices[i]+dp[i-1][0]);
(3)dp数组如何初始化
根据递推公式,两者都是从dp[0][0]和dp[0][1]开始推导出来,所以,dp[0][0]-=prices[0]
表示第0天不持有股票,所以现金是0,dp[0][1]=0;
(4)确定遍历顺序
dp[i]都是由dp[i-1]推出来的,所以一定是从前向后遍历
(5)举例推导数组
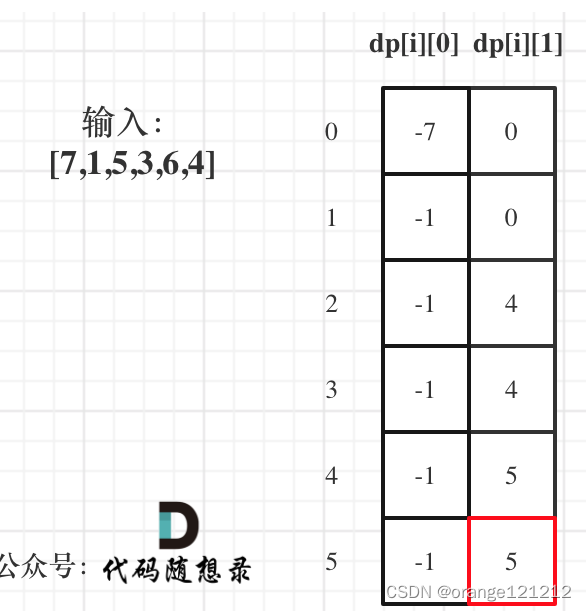
根据prices=[7,1,5,3,6,4]可得
dp[0][0]=-7; dp[0][1]=0
dp[1][0]=-1; dp[1][1]=max(0,-6)=0
dp[2][0]=-1; dp[2][1]=max(0,4)=4
dp[3][0]=-1; dp[3][1]=max(4,2)=4
dp[4][0]=-1; dp[4][1]=max(4,5)=5
dp[5][0]=-1; dp[5][1]=max(5,3)=5
本题有多种方法可解决,动态规划比较难构思,第二题不做学习