一、概述
机器学习大致会被划分为两类:监督学习,无监督学习
1.1 监督学习
监督学习其实就是,给计算机一些输入x和正确的输出y(训练数据集),让他总结x->y的映射关系,从而给他其他的输入x,他能预测出较为准确的y。
接下来举一些监督学习的简单示例:
1.1.1 回归算法
给你训练数据集(x,y),拟合出一条直线或者曲线,能够完美的反应x和y的关系,从而给你其他的数据x,能够通过拟合线计算出y。
1.1.2 分类算法
通过某些特征,将数据进行分类。
1.2 无监督学习
给你一些数据,算法会自动帮你划分数据。(与分类算法的区别:分类算法中,已经对数据x打上标签y,对这些标签进行分类。但是无监督学习,数据没有标签,算法自动对他进行划分,即只有输入x,没有输出y)
1.2.1 聚类算法
获取没有标签的数据,并尝试自动将他们分组到集群中。
1.2.2 降维算法
二、单变量线性回归模型
给出训练集(x,y),拟合出一条直线f(x)=wx+b,能够将测试集xi带入,计算出yi。
2.1 代价函数
w,b被称为模型参数,我们需要定义代价函数,来说明w,b拟合效果的好坏。
假设m表示训练集的大小,y-hat表示计算值,y表示真实值
成本函数:J(w,b)=1/2m(i=1.....m)(y-hati-yi)^2,(用计算值-真实值的平方 的平均值来估计w,b拟合效果的好坏)这里不是除以m而是2m,是为了方便后续的计算,不再除以2也是可以的。他也被称为平方误差成本函数。
在机器学习中,会有不同定义的成本函数,平方误差成本函数是其中之一,且效果好。
我们需要根据成本函数、训练数据,来计算出可以使cost最小化的模型参数w和b。
将w,b,J画成三维图,发现是一个碗的形状。我们将碗用J的等值面切割,会得到等高线图,他表示不同的(w,b)会有相同的J。越靠近等高线图的中心,J会越小。

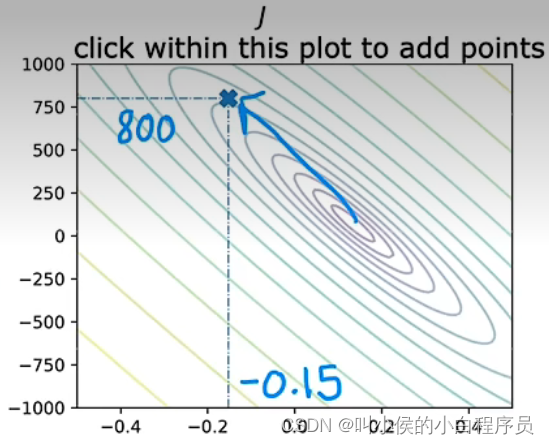
我们需要一个高效的算法,帮助计算最优模型参数。梯度下降法是个好方法。
2.2 梯度下降法
梯度下降法适用于求任何函数的最小值。步骤如下:
- 确定想要最小化的函数J(w,b)
- 设置w,b的初始值(一般初始化为w=0,b=0)
- 每次改变w,b,使J一直变小
- 直到J稳定或接近最小值

梯度下降法的简单理解:如图所示,当站在最高处,环绕360°,选择一个方向,可以使我迈出一小步,却能更快接近谷底,这个方向就是梯度下降最快的方向。到达下一个点后,继续环绕360°,选择一个最快接近谷底的方向。。。。如此反复,就能到达谷底。

当选择不同的初始值,使用梯度下降法可能会到达不同的谷底,这被称为局部最小值。
2.2.1 梯度下降法的实现
执行第三步骤时:给w赋值成 这里的
这里的表示学习率。学习率通常是0-1之间的小正数,他的作用是控制下坡的步幅。
同理需要更新b值。值得注意的是,更新的步骤要合理,如下图所示,左边是正确的,右边是错误的,这是因为,更新b时需要计算J对b的偏导数,此时需要用到w的原始值。

2.2.2 学习率
学习率对实现梯度下降的效率有巨大的影响。若学习率太小,到达最低点需要很多步骤,效率低;若学习率太大,梯度下降法可能会越过最低点,甚至无法收敛。
2.2.3 批量梯度下降
批量梯度下降指的是,在梯度下降的每一步中,我们都查看所有的训练示例,而不仅仅是训练数据的一个子集。
其他版本的梯度下降,在每个更新步骤查看训练数据的较小子集,而不是查看整个训练集。
三、多元线性回归
3.1 多维特征
现在有多个输入x1,x2......xn,一个输出y,怎么实现线性回归呢?
拟合函数(
)=w1x1+w2x2+w3x3+w4x4+b=
+b
在多元线性回归(多变量线性回归)中,应该使用矢量化的方法来简化表达和加快计算速度。
3.2 用于多元线性回归的梯度下降法
如下图,左边是原始版本,右边是矢量化版本的表达方式:

如下图,左边是单元线性回归更新模型参数的公式,右边是多元线性回归的:

3.2.1 特征缩放
在面对多维特征问题的时候,我们要保证这些特征都有具有相近的尺度,这会帮助梯度下降算法更快的收敛。
对于多维特征x1,x2......xn,每个特征的值域不同,有的特别小,有的很大。放到特征散点图中,可以看到,值域大的特征宽泛,值域小的窄瘪。放到等高线图中可以看到,参数小的(特征值大,因此参数会小)等高线窄(因为参数w1对应地特征值大,w1的一点点小改动,可能会对拟合函数f产生较大影响),参数大的(特征值小,因此参数较大)等高线宽,总体呈现出一种压扁的椭圆形状。

由于等高线又高又瘦,梯度下降法会在找到最小值之前来回弹跳很长时间。 因此我们需要做特征缩放,使每个特征的值域在0-1之间。下图是特征缩放前后散点图和等高线图的变化。
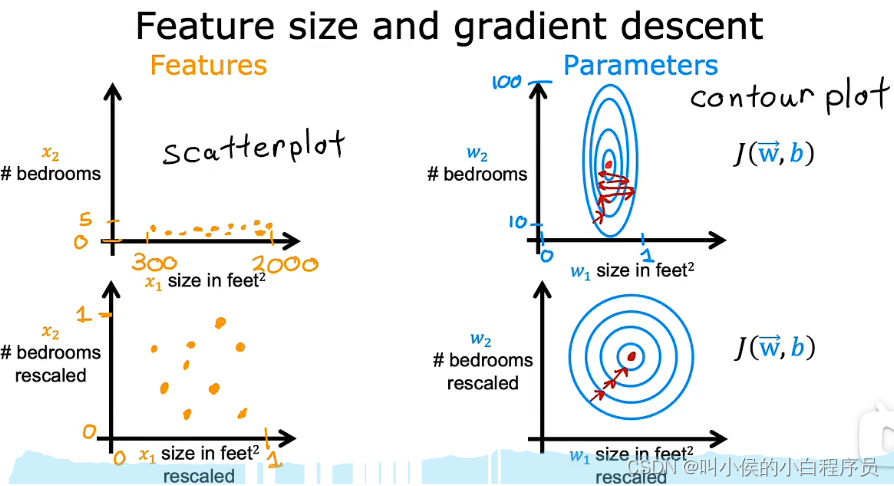
如何实现特征缩放呢?
方法一:每个特征值除以值域的最大值
方法二:均值归一化,每个特征值减去均值,在除以值域的范围(最大值-最小值)
方法三:Z分数归一化,每个特征值减去均值,再除以标准差
我们只要保证每个特征的值域在一个合理的范围就可以,如果某个特征的值域偏大或者偏小,就可以对他进行特征缩放,从而保证梯度下降法可以更快的收敛。
3.2.2 如何判断梯度下降是否收敛
方法一:
绘制学习曲线,横轴表示梯度下降算法的迭代次数,纵轴表示成本函数J的大小,如下图所示:
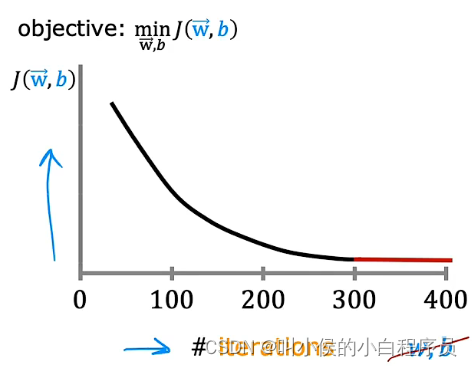
如果梯度下降正常工作,那么成本J每次都应该减少;若J在一次迭代后增加,这意味着选择不当(通常是
太大或者代码存在错误)。在迭代300次以后,成本J基本就稳定不变了,这意味着梯度下降算法收敛了。
方法二:
自动收敛测试,设置一个很小的量,当J在一次迭代后减小的幅度小于
,就将其判定为收敛。
3.2.3 如何设置学习率
如果您绘制多次迭代的成本并注意到成本有时上升有时下降,您应该将其视为梯度下降无法正常工作的明显迹象。说明可能学习率太大,或者代码中有错误。

若学习率太小,J下将会非常缓慢。所以我们应该先选一个非常小的学习率,然后逐步放大,直到不能再放大,就能找到最合适的学习率。
3.3 正规方程
梯度下降是最小化成本函数J以找到w和b的好方法,但还有另一种算法----正规方程,它仅适用于线性回归,不需要迭代梯度下降算法。正规方程法的一些缺点是:首先,与梯度下降不同,这不会泛化到其他学习方法;其次,若特征很多,计算效率低。
不需要要了解这种方法的具体实现细节,我们学会调用库函数就可以了!!!
3.4 特征工程
特征的选择对学习算法的性能具有较大的影响。
比如说估计房子的价格,目前有两个特征:房子的宽度W、长度L。我们可以设计拟合函数为=w1x1+w2x2+b;
我们可以设计第三个特征:房子的占地面积S=W*L,拟合函数变成=w1x1+w2x2+w3x3+b;
我们刚才所做的,创建一个新特征是所谓的特征工程的一个例子,你可以利用你对问题的知识或直觉来设计新特征(通常是通过转换或组合问题的原始特征)来使学习算法做出更准确地预测。
3.5 多项式回归
前面所学的单变量线性回归、多元线性回归,都是拟合为直线。但是假如只有一个特征x,可能呈现的不是直线的模型,这时候就需要用到多项式回归、
、
等。
四、逻辑回归
今天开始我们将学习监督学习的第二大类---分类算法,其中逻辑回归是经典算法之一。只有两种可能输出的分类问题-----二元分类。
介绍逻辑回归之前,先了解一个函数,sigmoid function(logistic function):
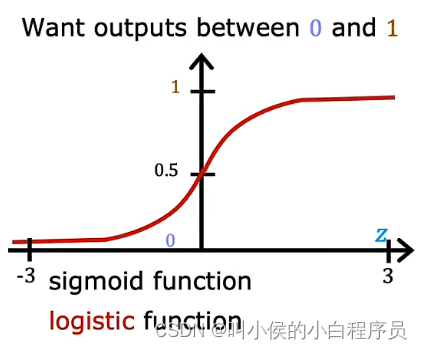
逻辑回归的数学公式:g(z)=
构建逻辑回归算法:
- 确定拟合函数,例如线性回归函数z=wx+b。
- 将拟合函数带入sigmoid 函数g(z)=
从此便构建出来逻辑回归算法=
。他的作用就是,输入特征集,输出0-1之间的数字。
4.1 决策边界
观察逻辑回归公式的曲线,将z输入,输出的数永远都是0-1之间的数据f。我们可以将输出f视为概率。例如f(z)=0.7 ,我们可以认为有0.7的概率预测是1。
当z=0时,f(z)=0.5,约定f0.5 时,输出1,f<0.5 时输出0。因此z=0是决策边界,由于z有不同的表达式,所以z=0边界的形状有各种各样的。
4.2 代价函数
之前讲线性回归时,代价函数是平方误差成本函数,但是这种方法不适用于逻辑回归。因为将代价函数J可视化后,可以看出,在线性回归中J呈现碗状,利用梯度下降算法,可以找到最小值;但是在逻辑回归中,J呈现锯齿状,有好多个局部最小值,所以不适合做逻辑回归的代价函数。

我们需要找到一个新的代价函数,来衡量参数w、b的优劣。如下图所示:若=1,成本函数为-log(f),f取值范围为0-1;因此成本函数呈现碗状,并且当预测值f越接近于1,成本函数J越小。同理
=0。
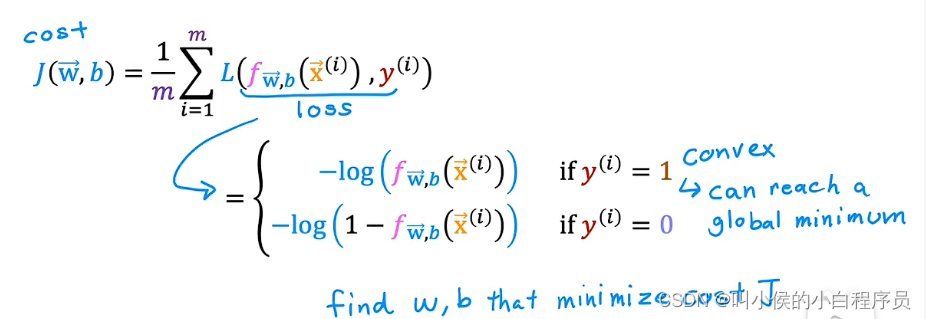
4.2.1 简化逻辑回归代价函数
将以上的函数简化成一个式子表达:

接下来可以推导出成本函数:
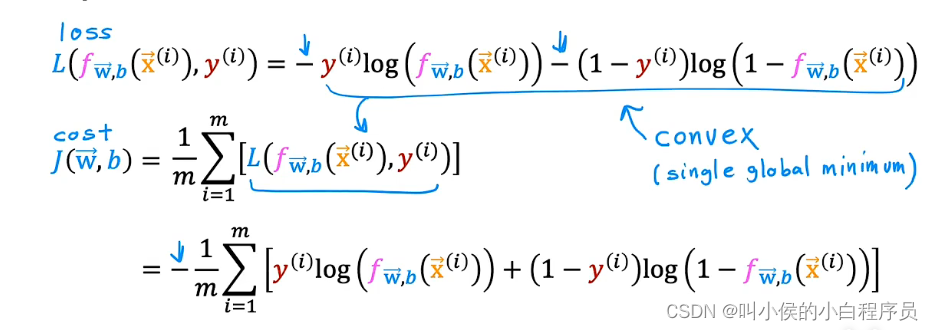
4.3 梯度下降
得到损失函数后,每次迭代更新参数w、b,每次都使J下降,直到J维持不变。

4.4 过拟合问题
使用线性回归预测房屋价格,输入特征是房子的面积,如下图所示:

肉眼可以看出,这不是一个好的模型,他不能很好地拟合训练数据,被称为模型对训练数据欠拟合(或者 算法具有高偏差)。
现在我们换成多项式回归的方法:

这个模型可以很好的拟合训练数据,学习算法能够很好地泛化,这意味着即使在它以前从未见过的全新示例上也能做出良好的预测。
现在使用四阶多项式拟合训练数据:
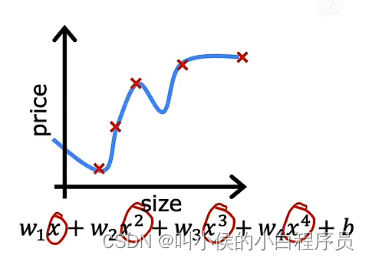
看起来,这条拟合曲线完美的通过了所有的训练示例, 成本函数为0。但是这是一条摇摆不定的曲线,甚至在某些地方,他预测的房屋价格比面积更小的房子的价格都低,这显然不符合常理。我们将这种情况称为过度拟合(或者 算法具有高方差)。
以上的问题同样会出现在分类算法中,下图中x1表示肿瘤大小,x2表示患者年龄,0表示良性肿瘤,+表示恶性肿瘤。下图从左到右分别是欠拟合、完美、过度拟合:

4.4.1 解决过拟合问题
方法一:
使用更多的训练数据集,学习算法将会适应一个波动较小的函数。

方法二:
减少特征,如果特征太多,但是没有足够多的训练数据,也可能会出现过度拟合的状况。选择最合适的一组特征来使用,也称为特征选择。
方法三,正则化:
正则化相对于方法二更加温和,他没有直接删除某些特征或多项式,而是将其参数w设置成一个非常小的数,以此来减少相应特征的影响力。从而曲线能很好的拟合训练数据。正则化的作用是,它可以让你保留所有特征,它们只是防止特征产生过大的影响(这有时会导致过度拟合)。

正则化的方法,只适用于正则化参数w,对于参数b基本没有什么作用。(加入特征很多,我们一时间无法准确判断哪些特征值得保留、哪些需要正则化)正则化的典型实现方式是惩罚所有的特征,或者更准确地说,惩罚所有的W参数,并且这通常会导致拟合更平滑、更简单、也不太容易过度拟合。
4.4.2 正则化
如下图所示:成本函数的左边是为了拟合训练数据,右边是正则化系数。分析的作用:当
等于0时,相当于对任何系数都没有正则化,曲线如下图蓝线所示(数据过度拟合);当
等于无穷大时,
的系数无穷大,那么求成本函数J最小值时,w一定会无限趋近于0,则f=b,曲线如下图紫色线所示,趋近于一条直线(欠拟合)。

因此 应该在0-无穷大之间,选择一个合适的数,平衡第一项和第二项。
4.4.3 用于线性回归的正则化方法
正则化线性回归的梯度下降算法:

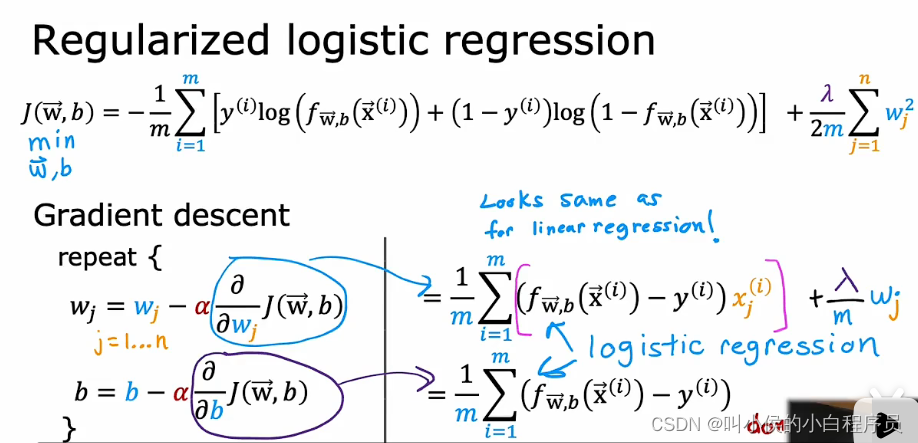
4.4.4 用于逻辑回归的正则化方法
逻辑回归的正则化表示的成本函数:

正则化逻辑回归的梯度下降算法: