算法通关村第19关【黄金】| 继续盘点高频动态规划dp问题

回文串专题

1.最长回文串

思路：

确定dp：dp[i][j]子串是否是回文串

确定递推公式：

例如：aa|cbc|aa dp[2][4] = dp[3][3] true

如果s[i] == s[j] 那么 dp[i][j] = dp[i+1][j-1]
否则dp[i][j] = false

确定初始化：dp[i][i] = true,一个字母都是回文

确定遍历顺序：子串从长度2开始一直到len长度，从小到大。i从小到大，不可以更换顺序

两个一组从头遍历到尾，三个一组从头遍历到尾，456....len个一组遍历到尾

class Solution {
    public String longestPalindrome(String s) {
        int len = s.length();
        if (len < 2) {
            return s;
        }
        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        boolean[][] dp = new boolean[len][len];
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }
        for(int l = 2;l<=len;l++){
            for(int i = 0;i<len;i++){
                int j = l + i - 1;
                if(j>=len){
                    break;
                }
                dp[i][j] = false;
                if(s.charAt(i) == s.charAt(j)){
                    if(j-i<3){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i+1][j-1];
                    }
                    if(dp[i][j]&&j-i+1>maxLen){
                        maxLen = j-i+1;
                        begin = i;
                    }
                }
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}

2. 分割回文串II

思路：

确定dp：dp[i][j]子串是否是回文串（上一问方法），f[i]第i个字符最少的分割次数

确定递推公式：

如果dp[0][i]为true说明当前整个字符串就是回文串不需要分割，那么 f[i] = 0
否则dp[0][i]为false说明当前字符串需要进行分割，对当前字符串进行遍历，从当前字符串第二个字符开始（第一个字母自身就是回文），是回文子串就分割，f[i] = Math.min(f[i]，f[j]+1)一直分割找到最小分割次数

确定初始化：f[i] = Integer.MAX_VALUE

确定遍历顺序：从前往后

class Solution {
    public int minCut(String s) {
        int len = s.length();
        boolean[][] dp = new boolean[len][len];
        for(int i = 0;i<len;i++){
            dp[i][i] = true;
        }
        //标记回文子串
        for(int l = 2;l<=len;l++){
            for(int i = 0;i<len;i++){
                int j = l + i - 1;
                if(j>=len){
                    break;
                }
                dp[i][j] = false;
                if(s.charAt(i) == s.charAt(j)){
                    if(j-i<3){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i+1][j-1];
                    }
                }
            }
        }
        //分割次数
        int[] f = new int[len];
        for(int i = 0;i<len;i++){
            f[i] = Integer.MAX_VALUE;
        }
        
        for(int j = 0;j<len;j++){
            if(dp[0][j]){
                f[j] = 0;
            }else{
                for(int i = 0;i<j;i++){
                    if(dp[i+1][j]){
                        f[j] = Math.min(f[j],f[i] + 1);
                    }
                }
            }
        }
        return f[len-1];
    }
}

双串典型问题

1.最长公共子序列

思路：

确定dp：dp[i][j] text1前i个字符和text2前j个字符最长公共子序列

确定递推公式：

如果s[i] == s[j]，dp[i][j] = dp[i-1][j-1]+1
否则，dp[i][j] = Max(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])

确定初始化：默认都是0

确定遍历顺序：从前往后

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        int[][] dp =new int[len1+1][len2+1];
        char[] s1 = text1.toCharArray();
        char[] s2 = text2.toCharArray();
        for(int i = 0;i<len1;i++){
            for(int j = 0;j<len2;j++){
                if(s1[i] == s2[j]){
                    dp[i+1][j+1] = dp[i][j] + 1;
                }else{
                    dp[i+1][j+1] = Math.max(dp[i][j+1],dp[i+1][j]);
                }
            }
        }
        return dp[len1][len2];
    }
}

2.编辑距离

思路：

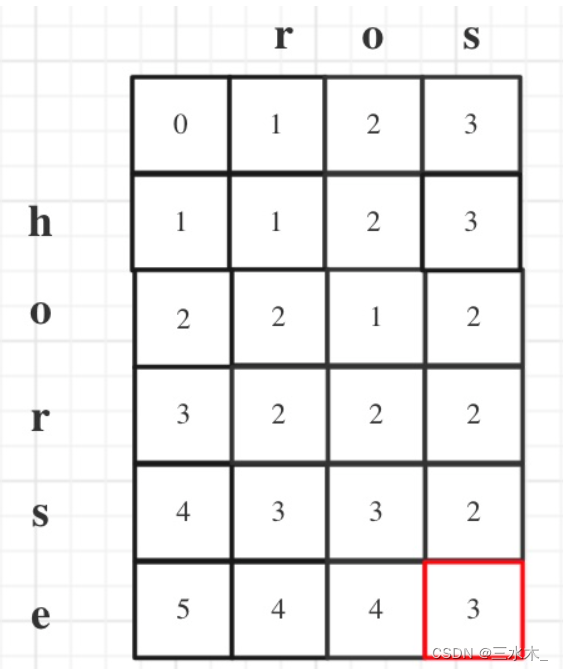
p[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

相等不相等两种情况：

if (word1[i - 1] == word2[j - 1])

那么就不用编辑，dp[i][j] = dp[i - 1][j - 1];

if (word1[i - 1] != word2[j - 1])

操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离再加上一个操作。即 dp[i][j] = dp[i - 1][j] + 1;
操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离再加上一个操作。即 dp[i][j] = dp[i][j - 1] + 1;
操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同。就是i-2和j-2的最近编辑距离再加上一个操作。因为此时是替换不是增删就是操作左上角元素

class Solution {
    public int minDistance(String word1, String word2) {
        char[] s1 = word1.toCharArray();
        char[] s2 = word2.toCharArray();
        int len1 = s1.length;
        int len2 = s2.length;
        int[][] dp = new int[len1+1][len2+1];
        for(int i = 0;i<=len1;i++){
            dp[i][0] = i;
        }
        for(int i = 0;i<=len2;i++){
            dp[0][i] = i;
        }
        for(int i = 0;i<len1;i++){
            for(int j = 0;j<len2;j++){
                if(s1[i] == s2[j]){
                    dp[i+1][j+1] = dp[i][j];
                }else{
                    dp[i+1][j+1] = Math.min(dp[i][j],Math.min(dp[i][j+1],dp[i+1][j]))+1;
                }
            }
        }
        return dp[len1][len2];
    }
}

3.正则表达式匹配

思路：

确定dp：dp[i][j] s前i个字符和p前j个字符是否能匹配

确定递推公式：

如果s[i] == p[j]，dp[i][j] = dp[i-1][j-1]
如果p[j] == '.'，dp[i][j] = dp[i-1][j-1]
如果p[j] == '*'
- 如果s[i] == p[j-1]||p[j-1] == '.' 匹配0个dp[i][j] = dp[i][j-2]，匹配1个dp[i][j] = dp[i][j-1]，匹配多个dp[i][j] = dp[i-1][j]
- 否则，匹配0个dp[i][j] = dp[i][j-2]

确定初始化：dp[0][0]=true 空串匹配

确定遍历顺序：从前往后

class Solution {
    public boolean isMatch(String s, String p) {
        int lens = s.length();
        int lenp = p.length();
        char[] sc = s.toCharArray();
        char[] pc = p.toCharArray();
        boolean[][] dp = new boolean[lens+1][lenp+1];
        dp[0][0] = true;
        for(int i = 0;i<=lens;i++){
            for(int j = 1;j<=lenp;j++){
                //从1开始防止越界
                if(i>0&&(pc[j-1] == '.'||pc[j-1] == sc[i-1])){
                    dp[i][j] = dp[i-1][j-1];
                }else if(pc[j-1] == '*'){
                    if(i>0&&(pc[j-2] == sc[i-1]||pc[j-2] == '.')){
                        //匹配0/1、多个，需要加上匹配0个，a ..* .*丢弃
                        dp[i][j]=dp[i][j-1]|dp[i-1][j]|dp[i][j-2];
                    }else{
                        dp[i][j] = dp[i][j-2];
                    }
                }
            }
        }
        return dp[lens][lenp];
    }
}

乘积最大子数组

思路：

确定dp：

dp[i]第i个字符最大乘积dp[i]=max(dp[i-1]*nums[i],nums[i])，这样忽略了负负得正的情况

max[i]当前子数组对应的最大乘积

min[i]当前子数组对应的最小乘积

确定递推公式：

三种情况取最大和最小

max[i] = Math.max(max[i-1]*nums[i],Math.max(min[i-1]*nums[i],nums[i]));

确定初始化：

max[0] = nums[0];
min[0] = nums[0];
int res = nums[0];

确定遍历顺序：从前往后

class Solution {
    public int maxProduct(int[] nums) {
        int[] max = new int[nums.length];
        int[] min = new int[nums.length];
        max[0] = nums[0];
        min[0] = nums[0];
        int res = nums[0];
        for(int i = 1;i<nums.length;i++){
            max[i] = Math.max(max[i-1]*nums[i],Math.max(min[i-1]*nums[i],nums[i]));
            min[i] = Math.min(max[i-1]*nums[i],Math.min(min[i-1]*nums[i],nums[i]));
            if(max[i]>res){
                res = max[i];
            }
        }
        return res;
    }
}

股票专题

1.买卖股票最佳时机

思路：prices[i] - min就是最大差价

class Solution {
    public int maxProfit(int[] prices) {
        int min = prices[0];
        int gap = 0;
        int res = 0;
        for(int i = 1;i<prices.length;i++){
            if(prices[i]<min){
                min = prices[i];
            }
            gap = Math.max(gap,prices[i]-min);
        }
        return gap;
    }
}

2.买卖股票的最佳时机II

思路：

确定dp：

dp[i][0]不持有当前股票所有资金

dp[i][1]持有当前股票所有资金

确定递推公式：

dp[i][0] = Math.max(dp[i-1][1] + prices[i],dp[i-1][0]); 前一天持有当天卖出/前一天也不持有
dp[i][1] = Math.max(dp[i-1][0]-prices[i] ,dp[i-1][1]); 前一天不持有当天买入/前一天也持有

确定初始化：dp[0][0]=0 dp[0][1] = -prices[0]当天买入

确定遍历顺序：从前往后

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1;i<prices.length;i++){
            dp[i][0] = Math.max(dp[i-1][1] + prices[i],dp[i-1][0]);
            dp[i][1] = Math.max(dp[i-1][0]-prices[i] ,dp[i-1][1]);
        }
        return dp[prices.length-1][0];
    }
}

3.买卖股票最佳时机III

思路：

确定dp：

dp[i][0][1]不持有当前股票所有资金,并且处于或者已完成第一次交易

dp[i][1][2]持有当前股票所有资金，并且处于或者已经完成第二次交易

确定递推公式：

dp[i][0][1] = Math.max(dp[i-1][0][1],dp[i-1][1][1]+prices[i]);继续不持有/第一次卖出
dp[i][1][1] = Math.max(dp[i-1][1][1],-prices[i]);继续持有/买入
dp[i][0][2] = Math.max(dp[i-1][0][2],dp[i-1][1][2] + prices[i]);继续不持有/第二次卖出
dp[i][1][2] = Math.max(dp[i-1][0][1]-prices[i],dp[i-1][1][2]);第二次买入/继续持有

确定初始化：dp[0][1][1]=-prices[0] dp[0][1][2] = -prices[0]持有状态说明买入

确定遍历顺序：从前往后

class Solution {
    public int maxProfit(int[] prices) {
        int[][][] dp = new int[prices.length][2][3];
        dp[0][0][0] = 0;
        dp[0][1][1] = -prices[0];
        dp[0][1][2] = -prices[0];
        for(int i = 1;i<prices.length;i++){
            dp[i][0][1] = Math.max(dp[i-1][0][1],dp[i-1][1][1]+prices[i]);
            dp[i][1][1] = Math.max(dp[i-1][1][1],-prices[i]);
            dp[i][0][2] = Math.max(dp[i-1][0][2],dp[i-1][1][2] + prices[i]);
            dp[i][1][2] = Math.max(dp[i-1][0][1]-prices[i],dp[i-1][1][2]);
        }
        return Math.max(dp[prices.length-1][0][1],dp[prices.length-1][0][2]);
    }
}

打家劫舍

思路：

确定dp：dp[i]到当前房屋所能获得的最大金额

确定递推公式：dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i]);偷当前房屋和不偷当前房屋

确定初始化：dp[0] = nums[0] dp[1] = max(nums[0],nums[1])

确定遍历顺序：从前往后

class Solution {
    public int rob(int[] nums) {
        if(nums.length == 1){
            return nums[0];
        }
        if(nums.length == 0){
            return 0;
        }
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] =  Math.max(nums[0],nums[1]);
        for(int i = 2;i<nums.length;i++){
            dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i]);
        }
        return dp[nums.length-1];
    }
}