文章目录
- 优化目标与评估指标
- 1. 优化目标
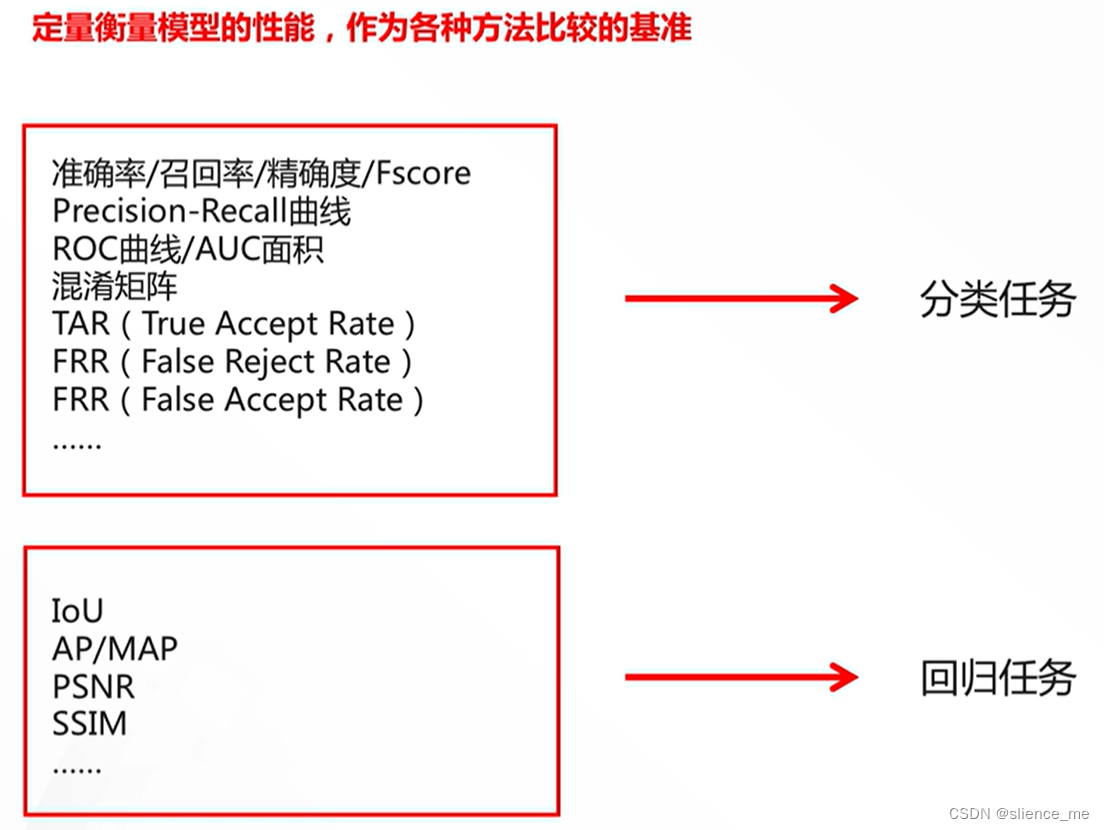
- 1.1 两类基础任务与常见优化目标
- 1.2 分类任务损失
- 0-1损失
- 交叉熵损失与KL散度
- softmax损失的理解与改进
- Hinge损失
- 1.3 回归任务损失
- L1/L2距离
- L1/L2距离的改进 Huber loss
- 2. 评测指标
- 2.1 分类任务中评测指标
- 准确率(查准率)/召回率(查全率)/精确度/PR曲线
- ROC曲线/AUC面积
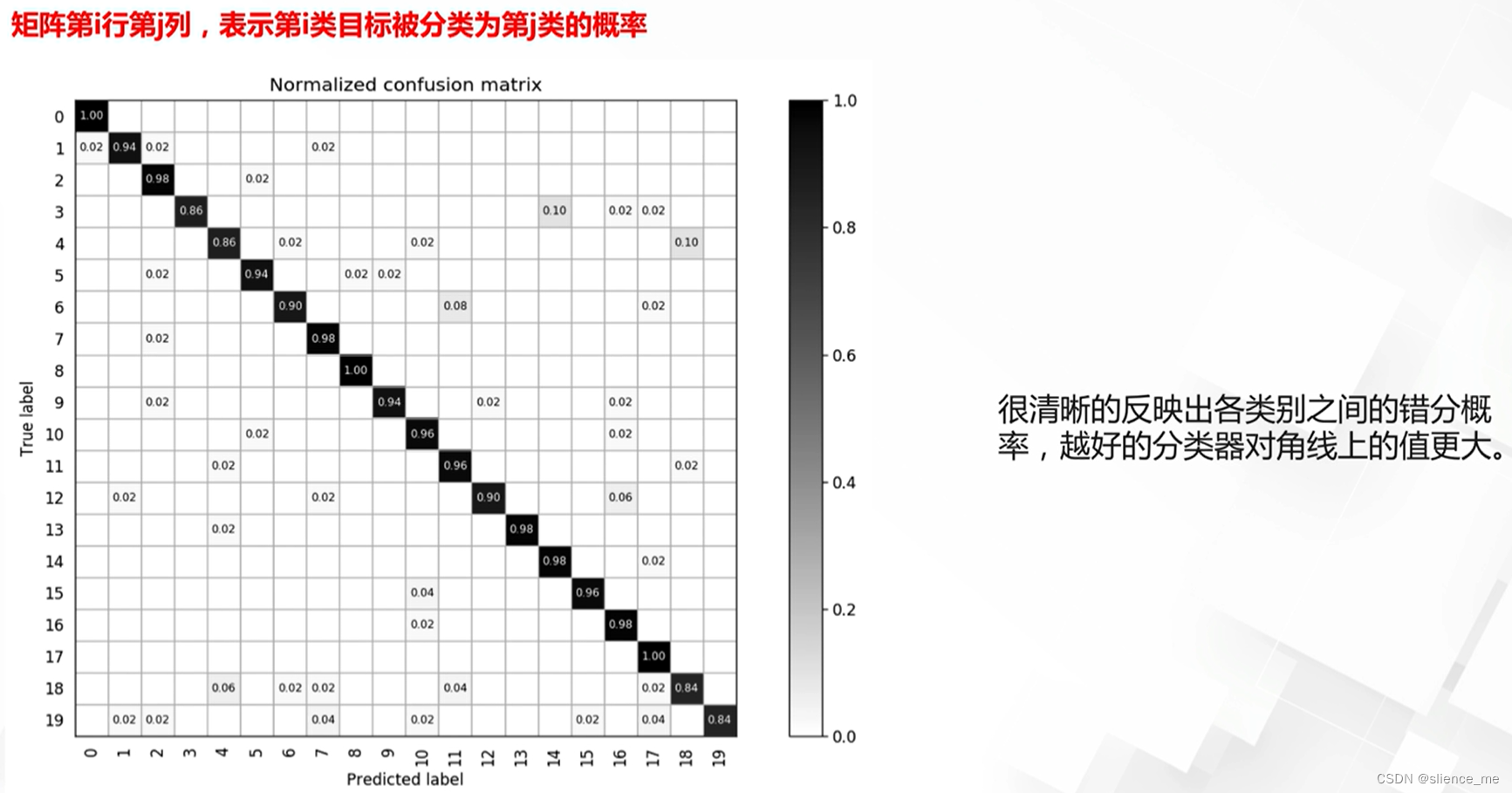
- 混淆矩阵
- 2.2 回归任务中的评测指标
- IoU(Intersection-over-Union)
- AP(Average Precision)/mAP
- 峰值信噪比PSNR
- 结构一致性相似SSIM
优化目标与评估指标
1. 优化目标
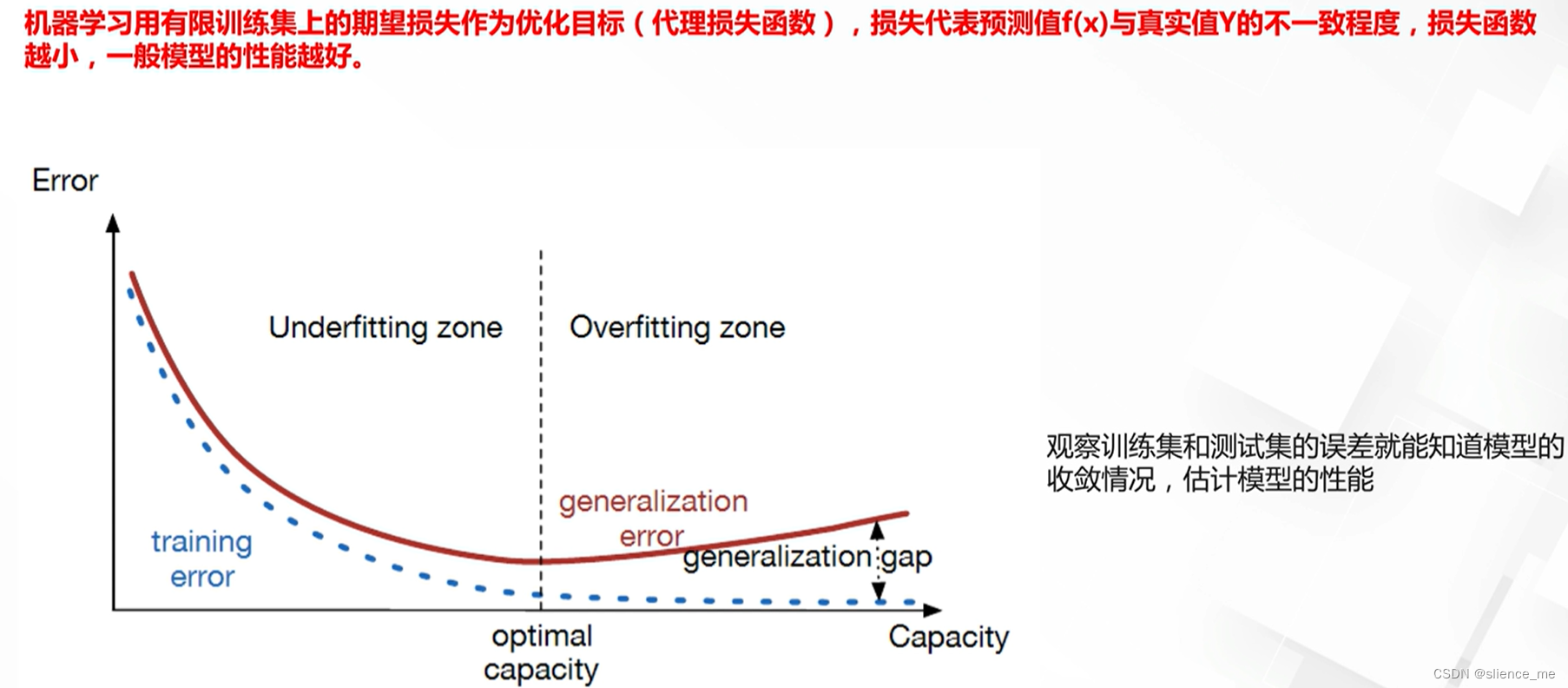
1.1 两类基础任务与常见优化目标
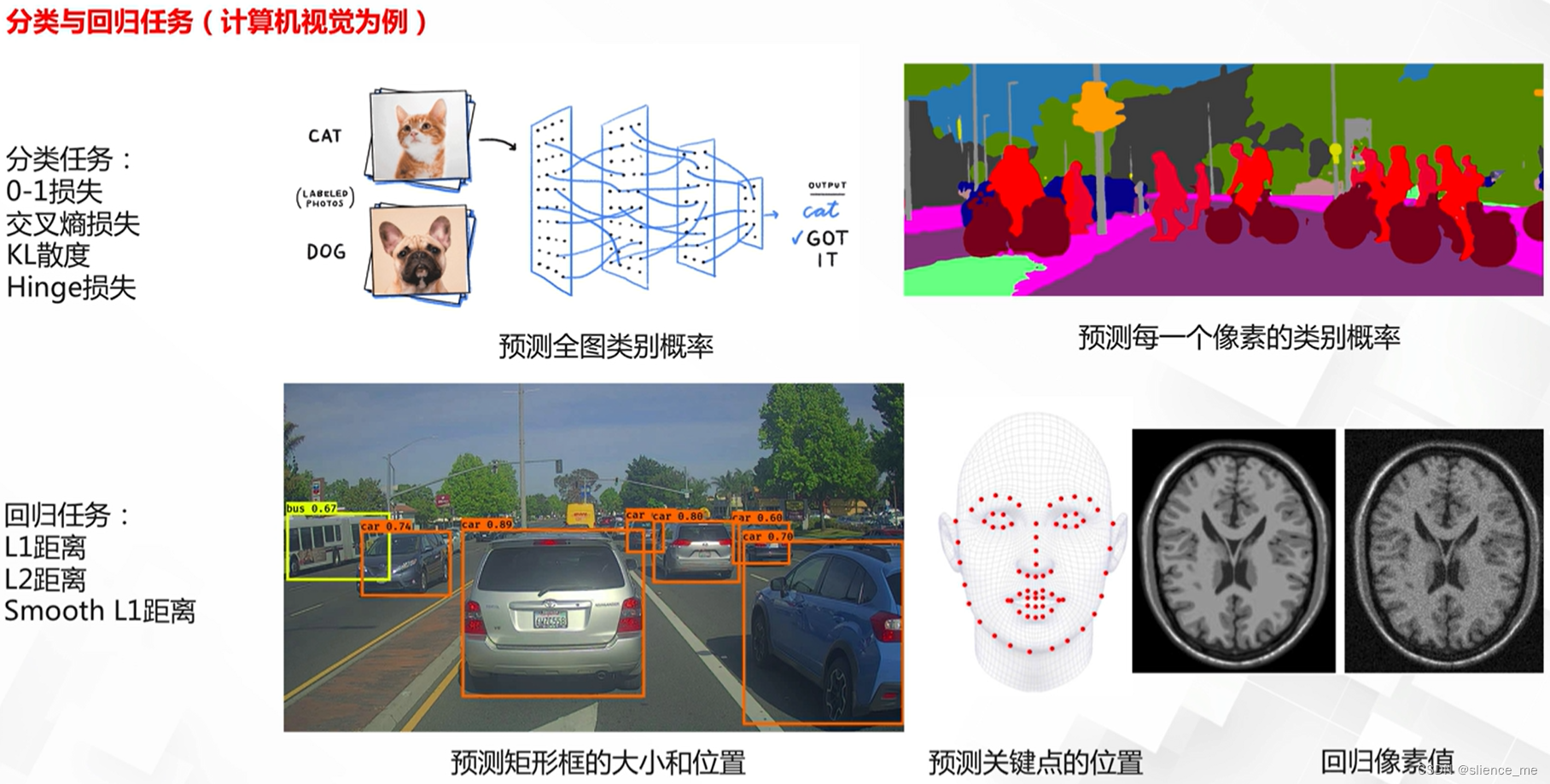
1.2 分类任务损失
在分类任务中,常见的损失函数包括交叉熵损失(Cross-Entropy Loss)、均方误差(Mean Squared Error, MSE)、Hinge损失(Hinge Loss)、对比损失(Contrastive Loss)、以及多类别对数损失(Multi-Class Log Loss)等。这些损失函数有不同的特点和用途,下面将简要介绍它们的区别:
交叉熵损失(Cross-Entropy Loss):
- 用于多类别分类任务。
- 计算模型的输出与真实标签之间的差异,鼓励模型为正确的类别分配更高的概率。
- 常见的变体包括二元交叉熵和多类别对数损失。
均方误差(Mean Squared Error, MSE):
- 通常用于回归任务,但也可以用于二元分类。
- 计算模型的输出和真实标签之间的平方误差,不适用于多类别分类。
Hinge损失(Hinge Loss):
- 通常用于支持向量机(SVM)等模型,也用于二元分类任务。
- 鼓励模型使正确类别的分数高于其他类别的分数,以增加分类的边际。
对比损失(Contrastive Loss):
- 用于度量学习和相似度学习任务。
- 鼓励相似样本之间的距离小于不相似样本之间的距离。
多类别对数损失(Multi-Class Log Loss):
- 类似于交叉熵损失,用于多类别分类任务。
- 计算模型对每个类别的对数概率,鼓励正确类别的概率高,常用于多标签分类任务。
- 这些损失函数的选择通常取决于任务的性质和所使用的模型。交叉熵损失在深度学习中应用最广泛,因为它在多类别分类任务中效果良好,且容易优化。但对于其他任务,不同的损失函数可能更为合适。根据任务的具体要求和数据类型,选择合适的损失函数非常重要。
0-1损失

交叉熵损失与KL散度
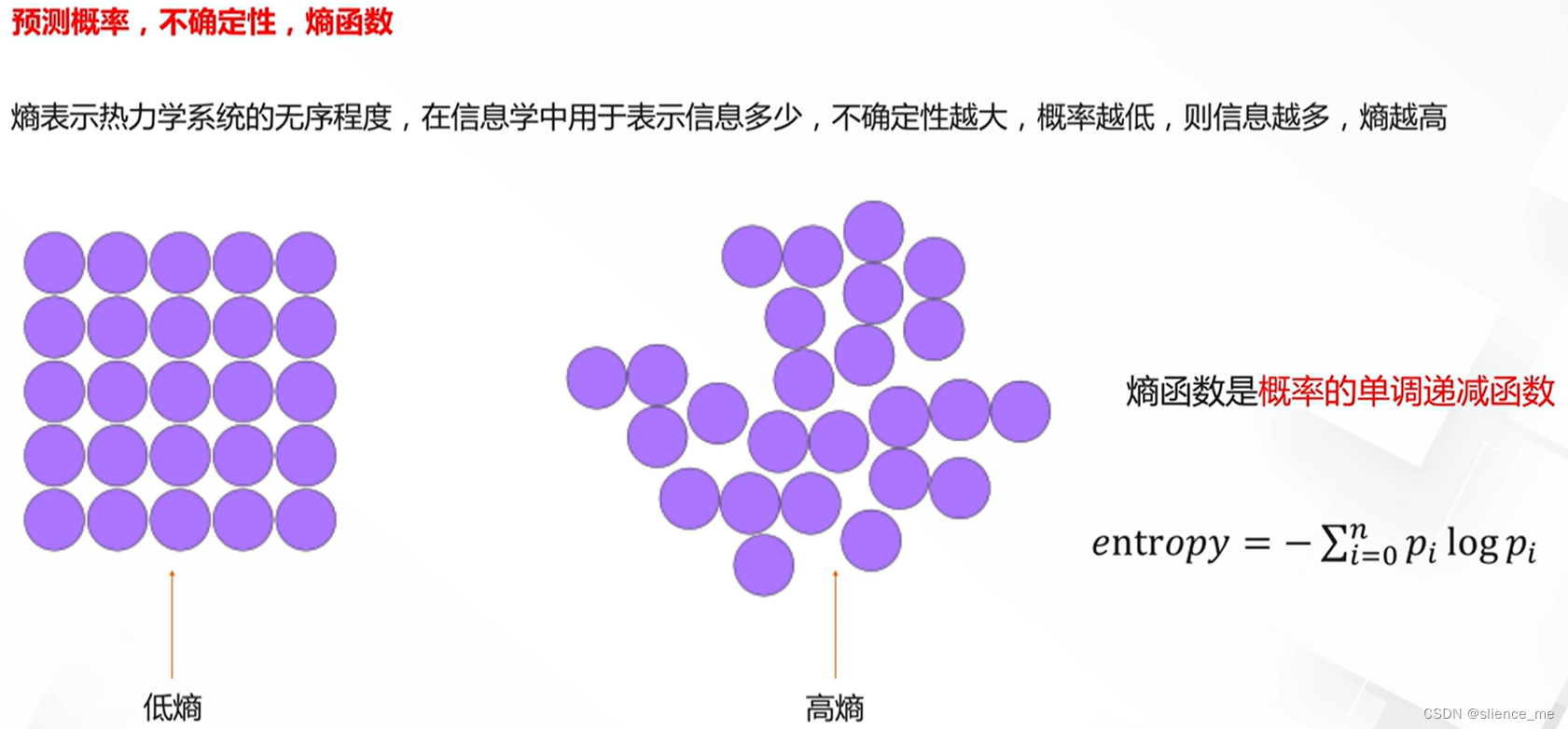

softmax损失的理解与改进
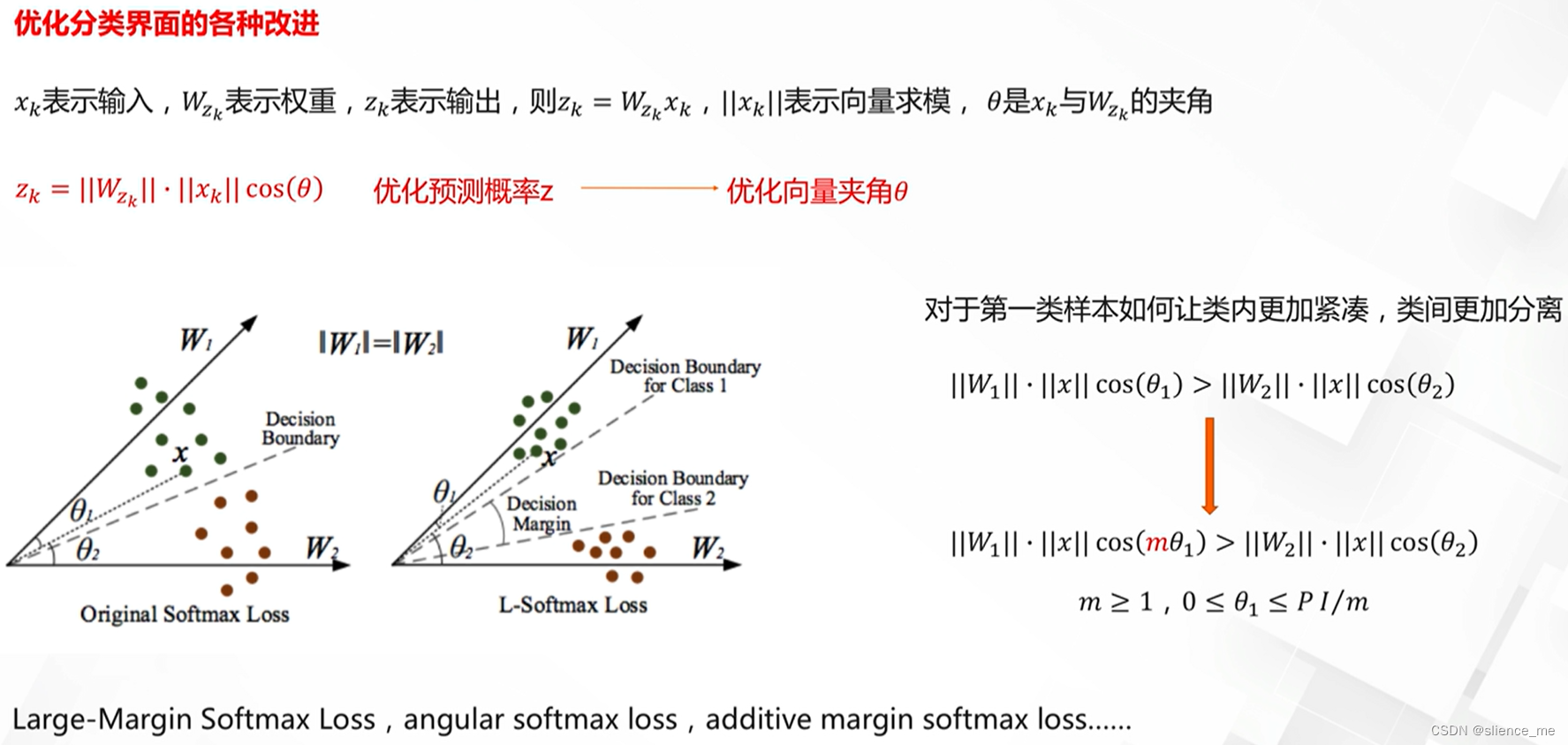
Hinge损失
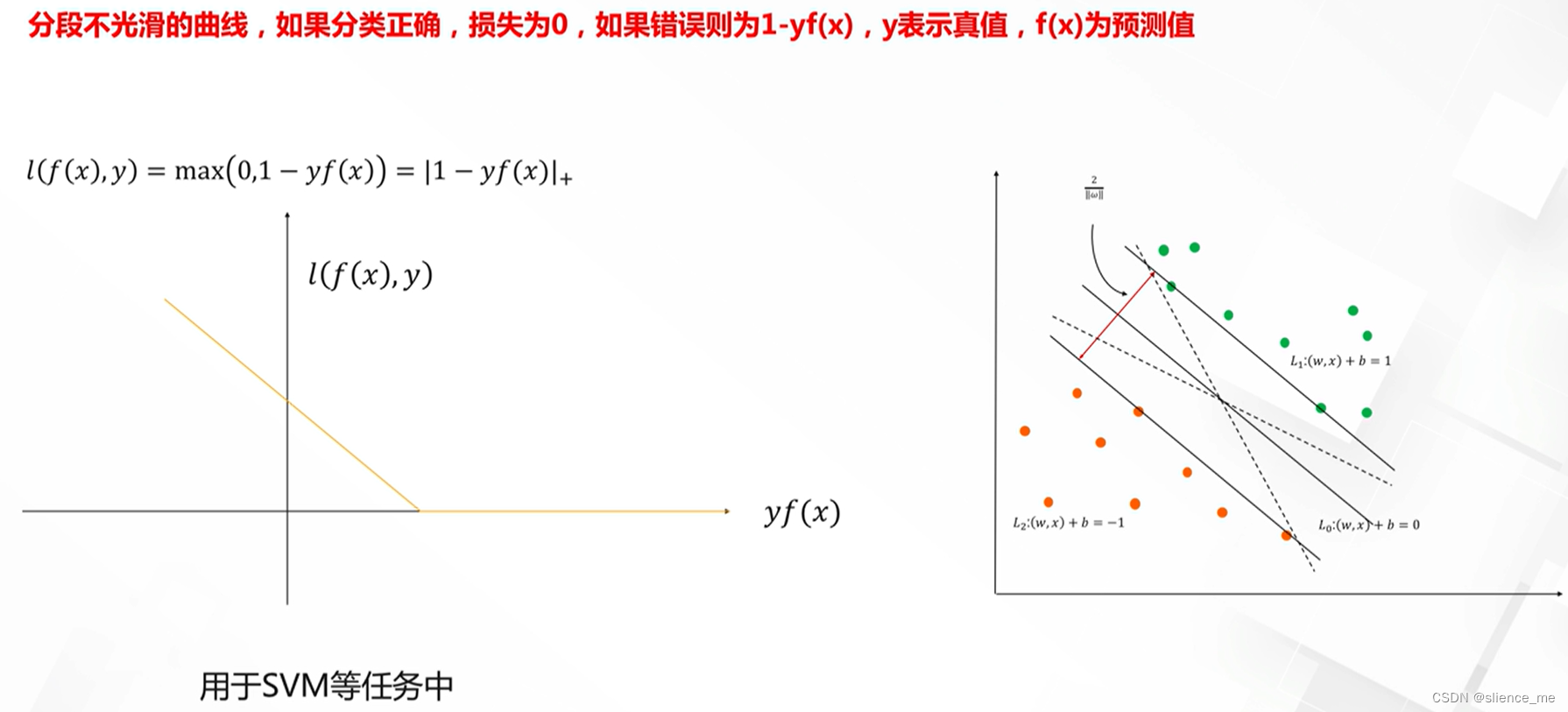
1.3 回归任务损失
在回归任务中,常见的损失函数包括均方误差(Mean Squared Error, MSE)、平均绝对误差(Mean Absolute Error, MAE)、L1损失(L1 Loss)、L2损失(L2 Loss),以及 Huber损失。以下是它们的主要区别:
均方误差(MSE):
- 计算模型的预测值与真实标签之间的平方差,然后取平均。
- MSE对异常值敏感,因为平方差会放大异常值的影响。
- MSE通常用于普通的线性回归任务。
平均绝对误差(MAE):
- 计算模型的预测值与真实标签之间的绝对差,然后取平均。
- MAE鲁棒性更好,不太受异常值的影响。
- MAE适用于对异常值敏感的任务,如金融风险评估。
L1损失(L1 Loss):
- 也称为绝对损失或L1范数损失,计算模型的预测值与真实标签之间的绝对差的总和。
- 类似于MAE,L1损失对异常值鲁棒性更好。
- L1损失通常用于稀疏建模和特征选择。
L2损失(L2 Loss):
- 也称为均方损失或L2范数损失,计算模型的预测值与真实标签之间的平方差的总和。
- L2损失对异常值敏感,因为平方会放大异常值的影响。
- L2损失通常用于正则化线性回归或神经网络。
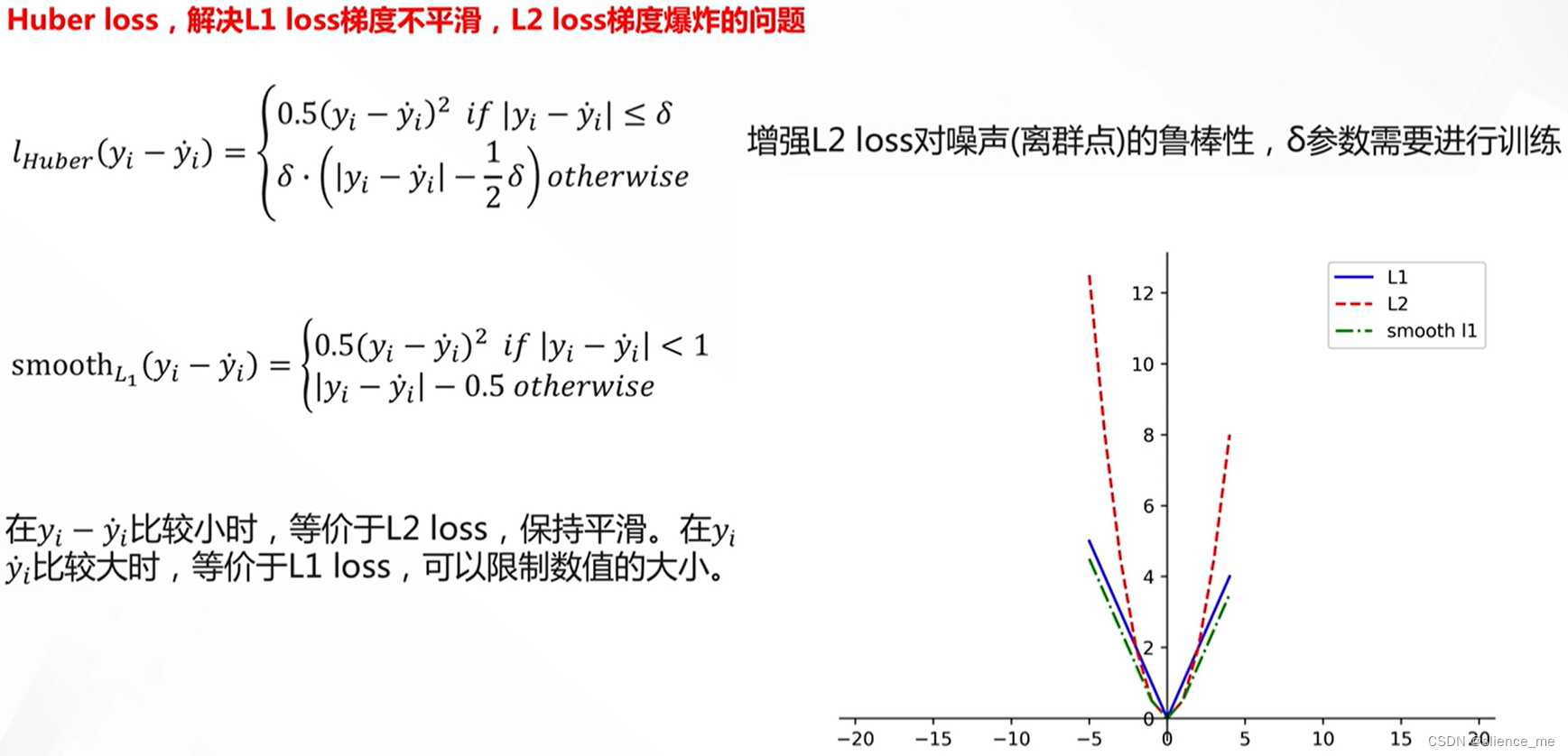
Huber损失:
- 一种折中方法,结合了L1和L2损失的特性。
- 在接近真实值时使用平方损失,远离真实值时使用线性损失,从而在一定程度上抵抗异常值。
总的来说,MSE和MAE分别度量了平方差和绝对差的平均值,对异常值的敏感性不同。L1损失和L2损失分别度量了绝对差和平方差的总和。Huber损失是这些损失函数的折中,既有MSE的平滑性,又有MAE的鲁棒性。损失函数的选择通常取决于任务的性质和数据的特点,以及对异常值的处理需求。
L1/L2距离

L1/L2距离的改进 Huber loss
2. 评测指标
在机器学习和深度学习任务中,有多种常见的评测指标用于度量模型的性能。这些指标根据任务类型和需求的不同而有所变化。以下是一些常见的评测指标:
1. 分类任务评测指标:
- 准确度(Accuracy):分类正确的样本数占总样本数的比例。
- 精确度(Precision):真正例(True Positives)占真正例和假正例(False Positives)之和的比例。用于度量模型预测正例的准确性。
- 召回率(Recall):真正例占真正例和假负例(False Negatives)之和的比例。用于度量模型检测正例的能力。
- F1分数(F1 Score):精确度和召回率的调和平均值,用于综合评估模型性能。
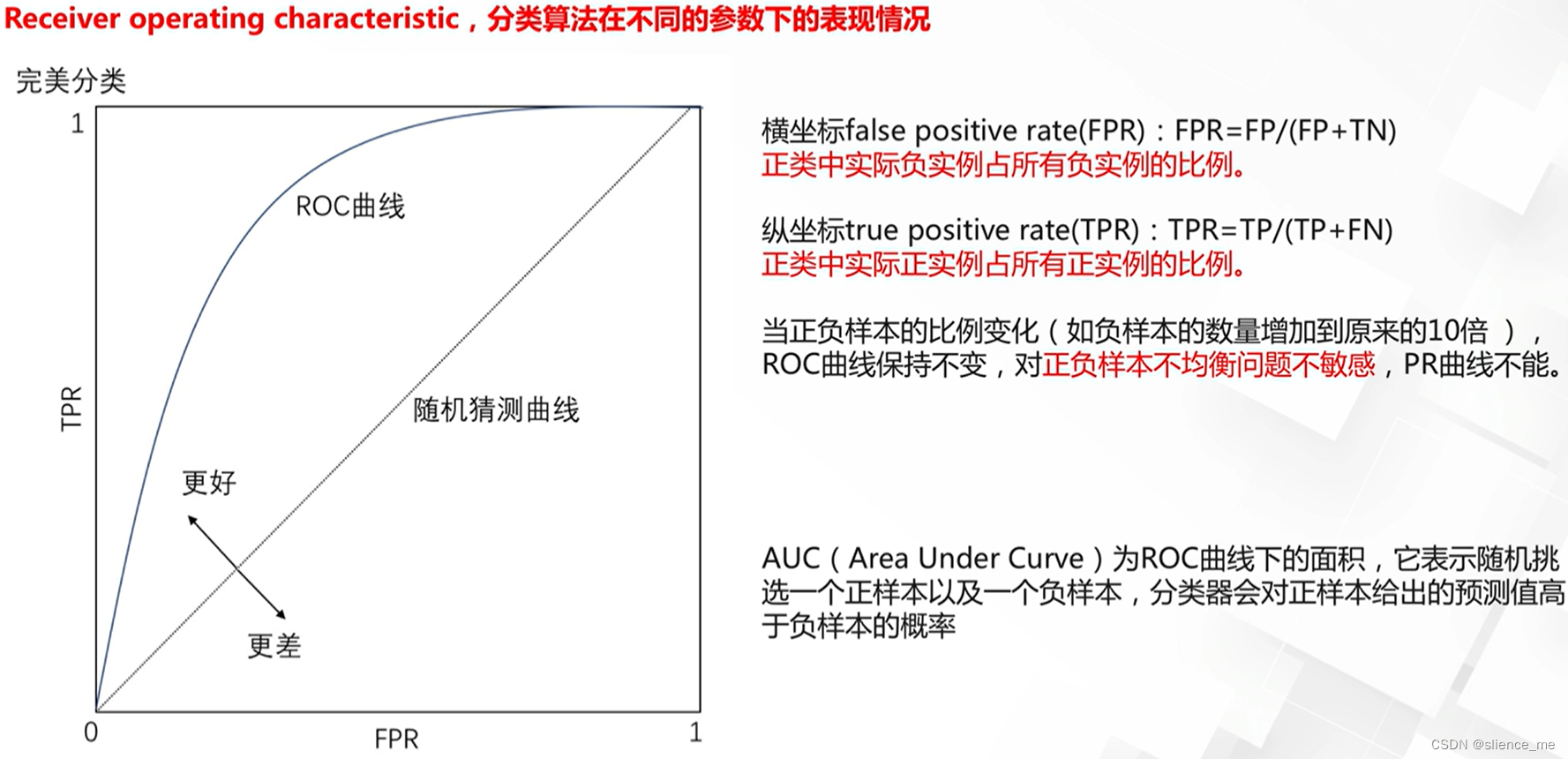
- ROC曲线(Receiver Operating Characteristic Curve):以不同的分类阈值绘制真正例率(True Positive Rate)和假正例率(False Positive Rate)之间的曲线。AUC(Area Under the Curve)用于度量ROC曲线下的面积。
- PR曲线(Precision-Recall Curve):以不同的分类阈值绘制精确度和召回率之间的曲线。AP(Average Precision)用于度量PR曲线下的平均精确度。
2. 回归任务评测指标:
- 均方误差(Mean Squared Error, MSE):预测值与真实值之间的平方差的平均值。
- 平均绝对误差(Mean Absolute Error, MAE):预测值与真实值之间的绝对差的平均值。
- 均方根误差(Root Mean Squared Error, RMSE):MSE的平方根,以与原始单位一致的方式度量误差。
- R平方(R-squared):用于度量模型对总方差的解释比例,值范围在0到1之间。
- 相关系数(Correlation Coefficient):用于度量模型预测值与真实值之间的线性关系。
3. 聚类任务评测指标:
- 轮廓系数(Silhouette Score):用于度量聚类的紧凑性和分离度,值范围在-1到1之间。
- Calinski-Harabasz指数:用于度量聚类的紧凑性和分离度,值越大表示聚类效果越好。
- Davies-Bouldin指数:用于度量聚类之间的平均相似性,值越小表示聚类效果越好。
- 这些评测指标根据任务类型和需求的不同,可以帮助您评估模型的性能和效果。选择适当的评测指标取决于具体任务的性质和目标。
2.1 分类任务中评测指标
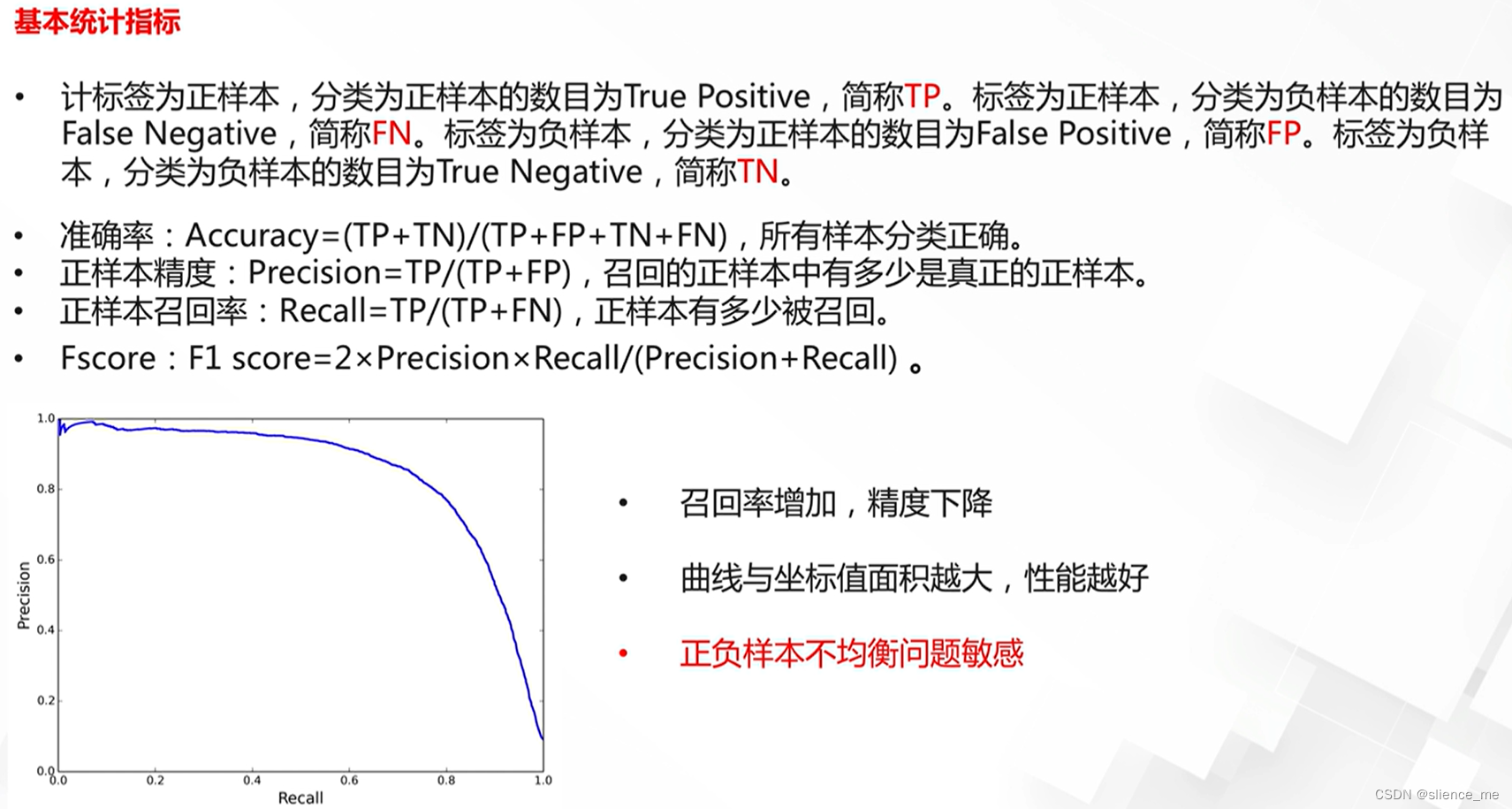
准确率(查准率)/召回率(查全率)/精确度/PR曲线
这些指标是用于评估分类模型性能的重要工具:
准确率(Accuracy):
- 准确率是指模型正确分类的样本数量与总样本数量的比例。
- 公式:准确率 = (真正例 + 真负例) / (总样本数)。
- 准确率度量了模型在所有类别上的分类正确性。然而,当类别分布不平衡时,准确率可能不是一个很好的度量标准。
召回率(Recall)(也称为查全率):
- 召回率是指模型成功检测到的真正例的数量与真正例的总数量之比。
- 公式:召回率 = 真正例 / (真正例 + 假负例)。
- 召回率度量了模型检测正例的能力。高召回率意味着模型能够捕捉更多的正例,但可能伴随着更多的假正例。
精确度(Precision):
- 精确度是指模型正确分类为正例的样本数量与所有分类为正例的样本数量之比。
- 公式:精确度 = 真正例 / (真正例 + 假正例)。
- 精确度度量了模型的预测中正例的准确性。高精确度意味着模型的正例预测更可信,但可能伴随着较低的召回率。
PR曲线(Precision-Recall Curve):
- PR曲线是一个图形表示,描述了不同分类阈值下精确度和召回率之间的关系。
- 横轴是召回率,纵轴是精确度。通过在不同阈值下计算精确度和召回率,可以绘制PR曲线。
- PR曲线可以帮助选择适当的分类阈值,以平衡精确度和召回率。面积下面积(AP)是PR曲线下的平均精确度,用于综合评估模型性能。
准确率、召回率和精确度是常见的二元分类评测指标,用于评估模型在正例和负例的分类中的表现。PR曲线则提供了精确度和召回率之间的权衡关系,有助于根据任务需求选择合适的分类阈值。这些指标对于不平衡数据集和不同任务的评估都非常重要。
真正例、真负例、假正例、假负例的区分
在二元分类问题中,混淆矩阵(Confusion Matrix)用于度量模型的分类性能,它包括四个主要元素,分别是真正例、真负例、假正例和假负例:
真正例(True Positives, TP):
- 真正例是指模型正确地将正例(Positive)样本分类为正例的情况。
- 换句话说,模型正确地检测到了正例。
真负例(True Negatives, TN):
- 真负例是指模型正确地将负例(Negative)样本分类为负例的情况。
- 换句话说,模型正确地识别了负例。
假正例(False Positives, FP):
- 假正例是指模型错误地将负例样本分类为正例的情况。
- 这种情况也被称为“误报”或“假阳性”。
假负例(False Negatives, FN):
- 假负例是指模型错误地将正例样本分类为负例的情况。
- 这种情况也被称为“漏报”或“假阴性”。
混淆矩阵的构成是为了帮助评估二元分类模型的性能,这四个元素允许您了解模型对正例和负例的分类准确性。基于这些元素,可以计算各种评测指标,如准确率、召回率、精确度等,以更全面地评估模型的性能。
看个样例:
让我们通过一个二元分类问题的示例来说明准确率、召回率、精确度和PR曲线的计算和解释。
假设我们正在解决一个垃圾邮件分类任务,其中模型的任务是将电子邮件标记为垃圾邮件(正例)或非垃圾邮件(负例)。
假设我们有以下混淆矩阵(Confusion Matrix):
True Positives (TP): 100
False Positives (FP): 20
False Negatives (FN): 10
True Negatives (TN): 300
基于这个混淆矩阵,我们可以计算以下指标:
准确率(Accuracy):
- 准确率表示模型正确分类的样本占总样本数量的比例。
- 准确率 = (TP + TN) / (TP + FP + FN + TN) = (100 + 300) / (100 + 20 + 10 + 300) = 400 / 430 ≈ 0.9302(约为93.02%)。
召回率(Recall):
- 召回率表示模型成功检测到的垃圾邮件(真正例)的数量与所有垃圾邮件的数量之比。
- 召回率 = TP / (TP + FN) = 100 / (100 + 10) = 100 / 110 ≈ 0.9091(约为90.91%)。
精确度(Precision):
- 精确度表示模型正确分类为垃圾邮件的样本数量与所有分类为垃圾邮件的样本数量之比。
- 精确度 = TP / (TP + FP) = 100 / (100 + 20) = 100 / 120 ≈ 0.8333(约为83.33%)。
PR曲线(Precision-Recall Curve):
- PR曲线通过在不同分类阈值下计算精确度和召回率来绘制。这里提供示例数据,而不是真正的PR曲线。
- 根据不同分类阈值,可以绘制不同点,然后连接这些点以获得PR曲线。
这些指标可以帮助您了解模型在分类任务中的性能。在这个示例中,模型的准确率为93.02%,召回率为90.91%,精确度为83.33%。通过PR曲线,您可以选择适当的分类阈值,以在精确度和召回率之间进行权衡,具体取决于任务需求。
ROC曲线/AUC面积
混淆矩阵
2.2 回归任务中的评测指标
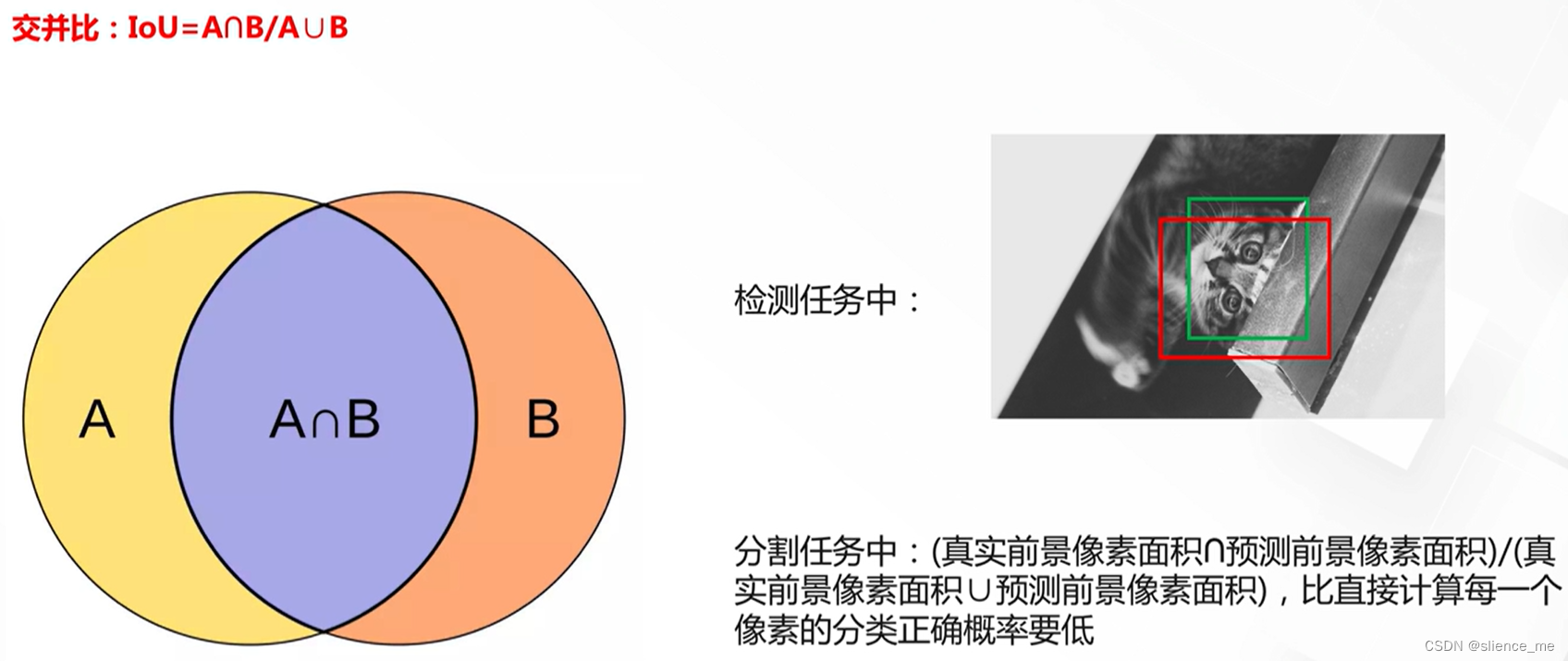
IoU(Intersection-over-Union)
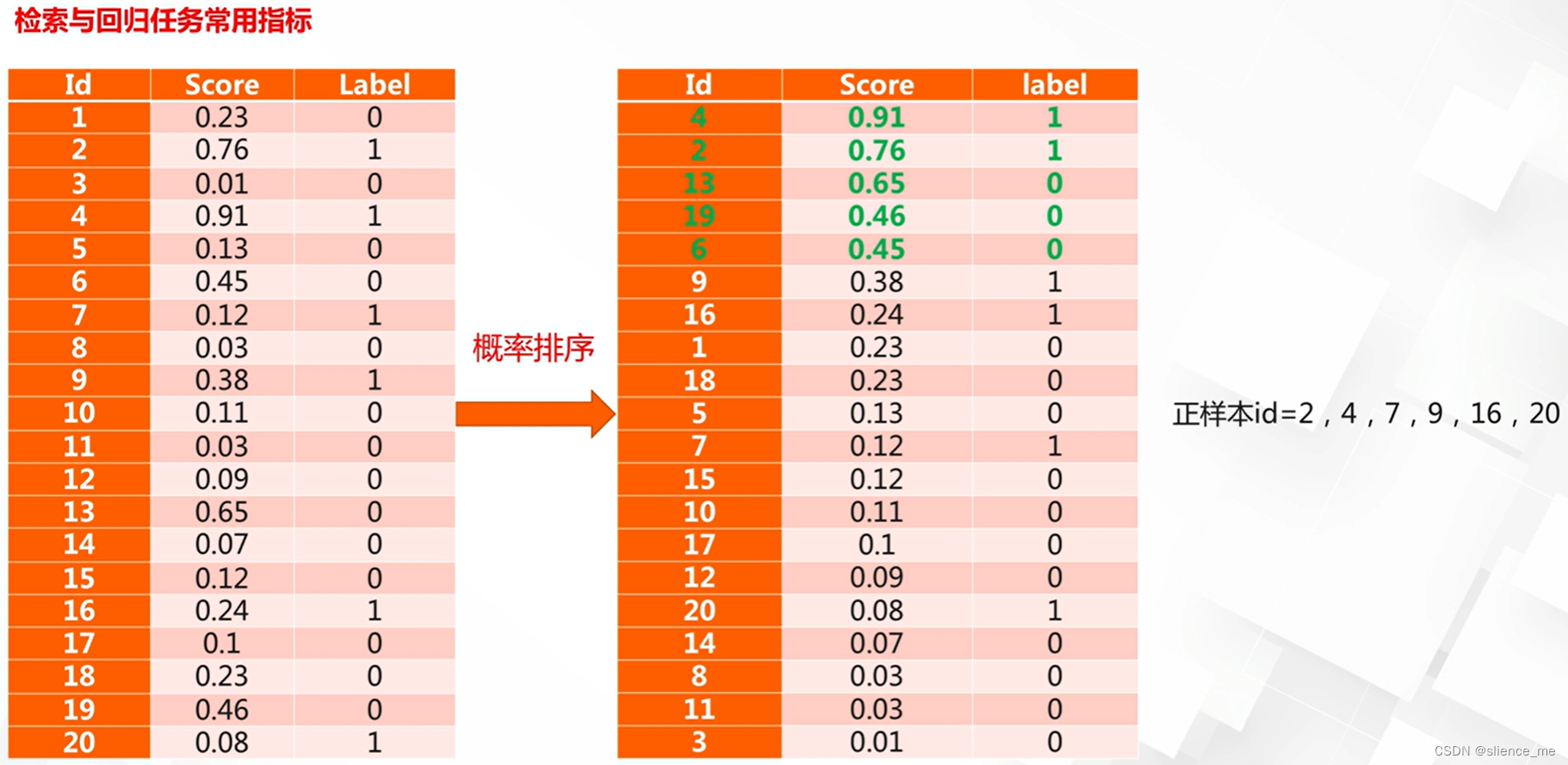
AP(Average Precision)/mAP
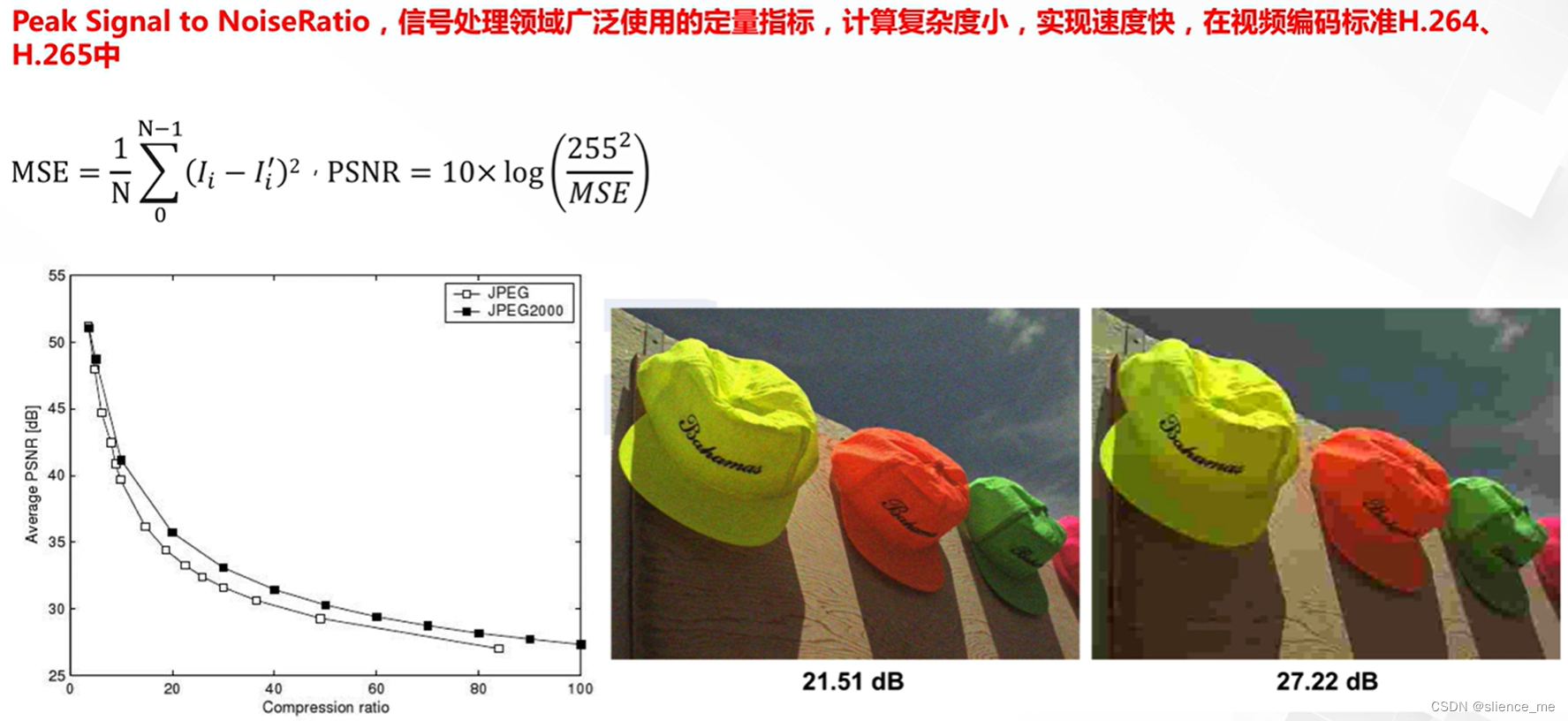
峰值信噪比PSNR
- PSNR越高,则代表图片质量越高
- 255表示灰度范围
- 在人眼感知的指标,表现不是很好
结构一致性相似SSIM

注: 部分内容来自阿里云天池