二叉树相关问题细谈递归

在这里插入图片描述

大家好，我是Dark Flame Master，今天给大家带来的介绍的是递归的思想，然后利用递归的方法实现建树的各个函数，例如节点个数，前中后序遍历，判断一棵二叉树是否为完全二叉树等，看完本文相信你会对递归思想有更加深入的认识。我将从基础说起，循循渐进，不断深化理解，同时呈上递归展开图帮助大家理解。

文章目录

- **递归**
- - 前中后序遍历
- 二叉树全局遍历问题
- - 树的节点个数
  - 叶子节点的个数
  - 第k层节点个数
- 查找某值并返回
- - 查找值为x的节点
- 判断树的结点的值相关问题
- - 单值二叉树
  - 相同的树
- 数的结构的问题
- - 翻转二叉树
  - 对称二叉树

递归

前言

递归的思想如其名就是递和归，一步一步展开，最后在合回去，从而解决问题，通过每次递归不断改变一定的数据，将大问题转化成一个一个和大问题相似的小问题来求解，只需要简短的程序，一步一步完成某个工作。
举一个生活中的例子
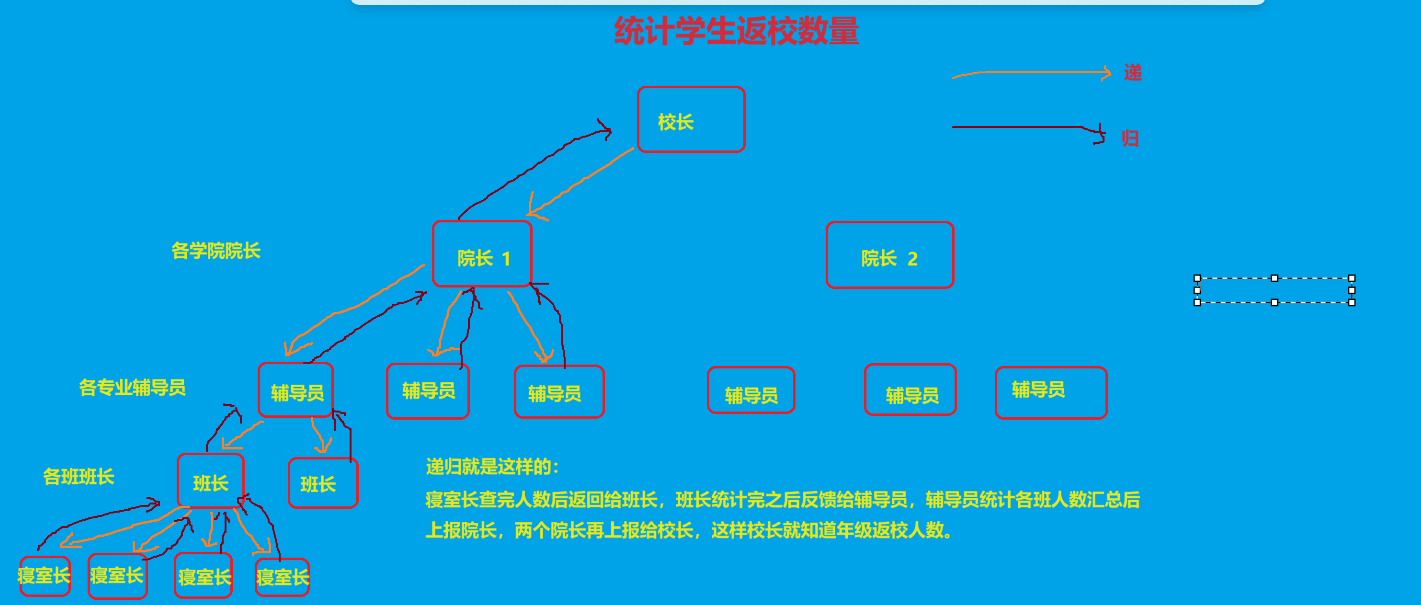
校长想要知道疫情返校人数，他可以一个一个寝室挨个查，也可以动用院长辅导员等人帮忙统计

递归就是如此

要学会递归，就要深刻了解递归的思想和方法，最重要的是他的逻辑性。

首先你要了解写出这个递归函数到底是用来做什么的，这是递归函数的第一要素，递归函数虽然短小精悍，但一定要明确知道自己的需求。
在递归的过程中会有前进段和返回段，满足一定的条件就进行前进，如果不满足则return返回，不能死递归下去，不然就会爆栈，这就是递归的第二要素。
再明确需求后，找出函数的等价关系式，这是递归的第三要素，会在后边的学习中进行说明。
以下两道题帮助理解，精彩还在后边。
求n的阶乘

int factorial(int n)
{
 if(n <= 1)
 	return 1;
 else
 	return n * factorial(n-1);
}

给这个函数传入参数，如果小于等于1，就返回1，假使传入的值为5，运行时return结果为nfactorical(4)，这个函数的返回值重新开辟了一个函数，传入值为4，这样一直递归，直至传入结果为1，当一个函数返回时，会回到之前进入函数的位置，然后在n=2的函数中继续return，直至函数结束。
通过不断地传递，当遇到限制条件后开始归，如图所示

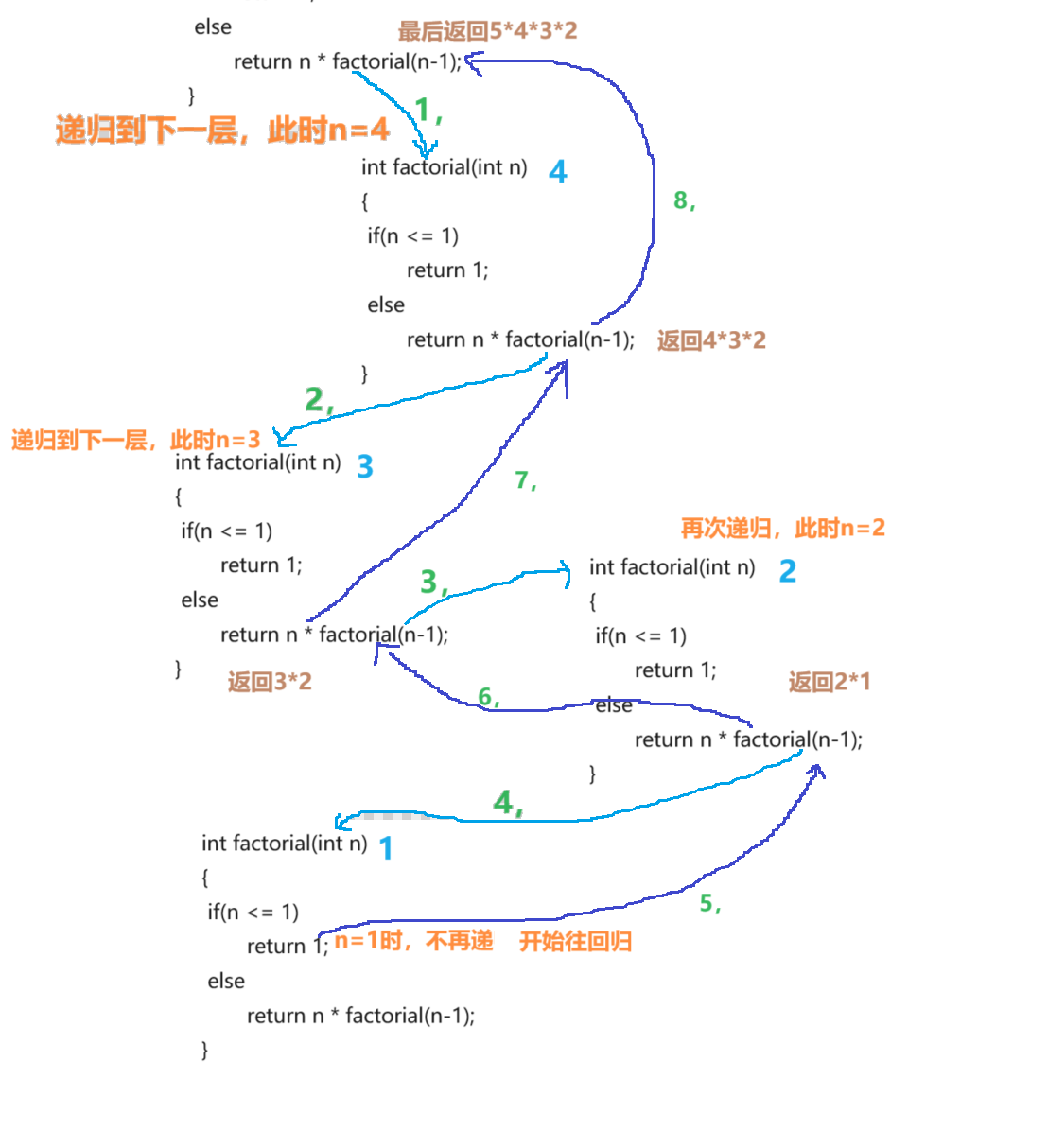
这个函数的作用是求n的阶乘，所以函数f(n)的等价关系式是nf(n-1)，在后边的函数中也都一样，改变的是n的值。
求第n个斐波那契数递归解法
在这里插入图片描述

int fib(int n)
{
 	if (n <= 2)         
 		return 1;
    else
    	return fib(n - 1) + fib(n - 2);
}

前两个数的结果为1，后边的数都是前两个相加，函数结束的标志是n<=2，函数的功能是实现找到第n个斐波那契数，要知道第n个斐波那契数，就要知道第n-1个斐波那契数和第n-2个斐波那契数，要知道第n-1个斐波那契数，就要知道第n-2和第n-3个斐波那契数，一直递归下来，可以看到，在求第n个斐波那契数时，第n-2个斐波那契数被求了两次，第n-3个斐波那契数被求了3次，如果n非常大的话，利用递归来查找结果，会多余计算很多次。
我们可以来实验一下

#include <stdio.h>
#include <stdlib.h>
int count = 0;//全局变量
int fib(int n)
{
	if (n == 3)
		count++;
	if (n <= 2)
		return 1;
	else
		return fib(n - 1) + fib(n - 2);
}
int main()
{
	fib(10);
	printf("%d", count);
	return 0;
}

运行后如图
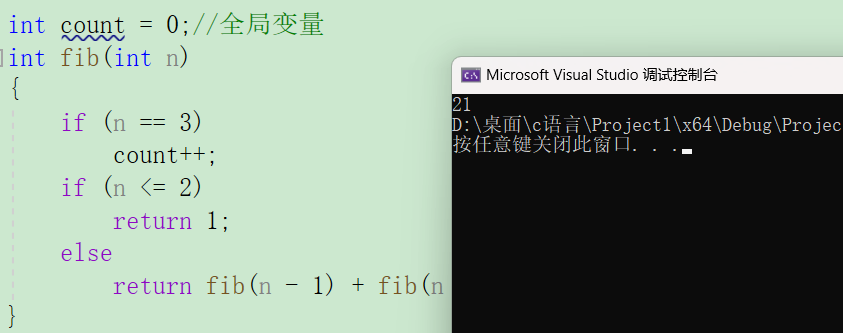
在这里插入图片描述
传入10，仅仅是3的斐波那契数就进行了21次，如果传入的值再大一点呢？
这个时候递归的弊端就显示出来了，虽然代码原理浅显易懂，但有些情况下要进行的运算太多了。

传入50跑了许久都跑不出来。如果数据再大一点的话，会一直开辟栈空间，知道栈空间被耗尽，造成栈溢出。
这种情况下我们还是利用非递归的方式来写。
第三个数是1+1，第四个数是2+1，只要保存更新两个相加数即可。

int fib(int n)
{
	int ret=1,pre=1;//结果
	int older_ret;//第一个加数
	while (n > 2)
	{
		n -= 1;
		older_ret = pre;
		pre = ret;//上一次的结果赋值
		ret = pre + older_ret;
	}
	return ret;
}

总结：

许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更为清晰。
但是这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性稍微差些。
当一个问题相当复杂，难以用迭代实现时，此时递归实现的简洁性便可以补偿它所带来的运行时开销。

但是当我们在计算二叉树相关的问题时，在遍历树的过程中递归就非常的好用。
从基本讲起，随后会有几道力扣题巩固理解

前中后序遍历

二叉树有三种遍历方式

1，前序遍历根，左，右。
2，中序遍历左，根，右。
3，后序遍历左，右，根。

结构体声明如下

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

其中根为子树的根节点，左为左孩子节点，右为右节点。
前序遍历

//前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%d ", root->data);//先访问该节点
	BinaryTreePrevOrder(root->left);//再访问左子树和右子树
	BinaryTreePrevOrder(root->right);
}

前序遍历就是先访问根节点，然后走左节点，再走右节点，首先访问该节点，然后找他的左，判断条件为如果该节点为空，就停止递，开始归。
假设我们已经有了一个二叉树
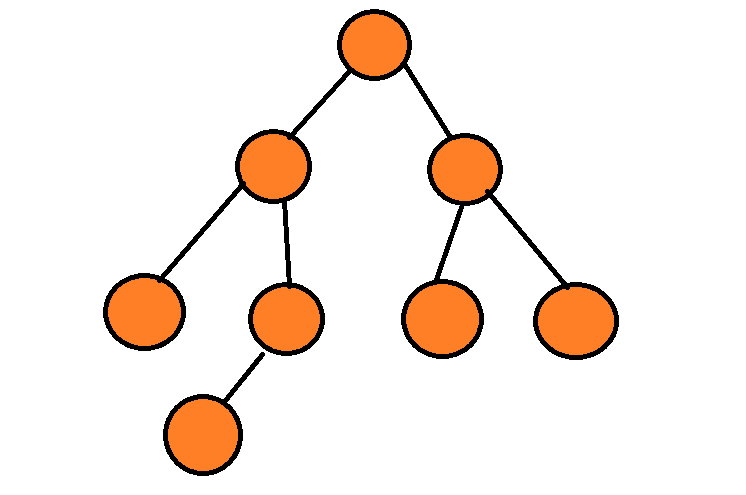
在这里插入图片描述

递归展开如下：
在这里插入图片描述
中序遍历和前序遍历相差不大

//中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreePrevOrder(root->left);//先访问左子树
	printf("%d ", root->data);//再访问该节点
	BinaryTreePrevOrder(root->right);//最后访问右子树
}

下边的问题都将利用这个二叉树来进行解释，这个树可以展现出我们会遇到的大多种情况。
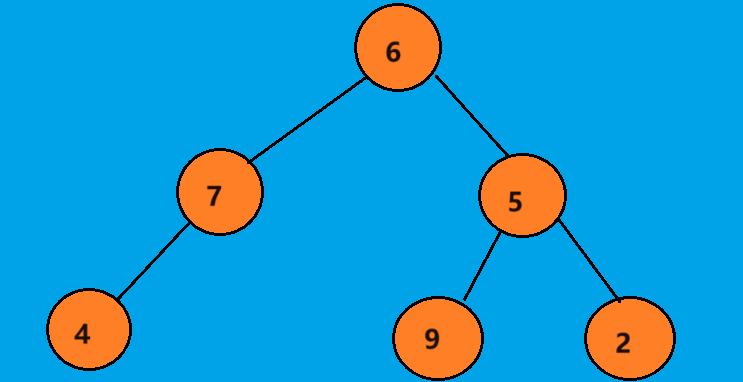
在这里插入图片描述

递归展开图如下
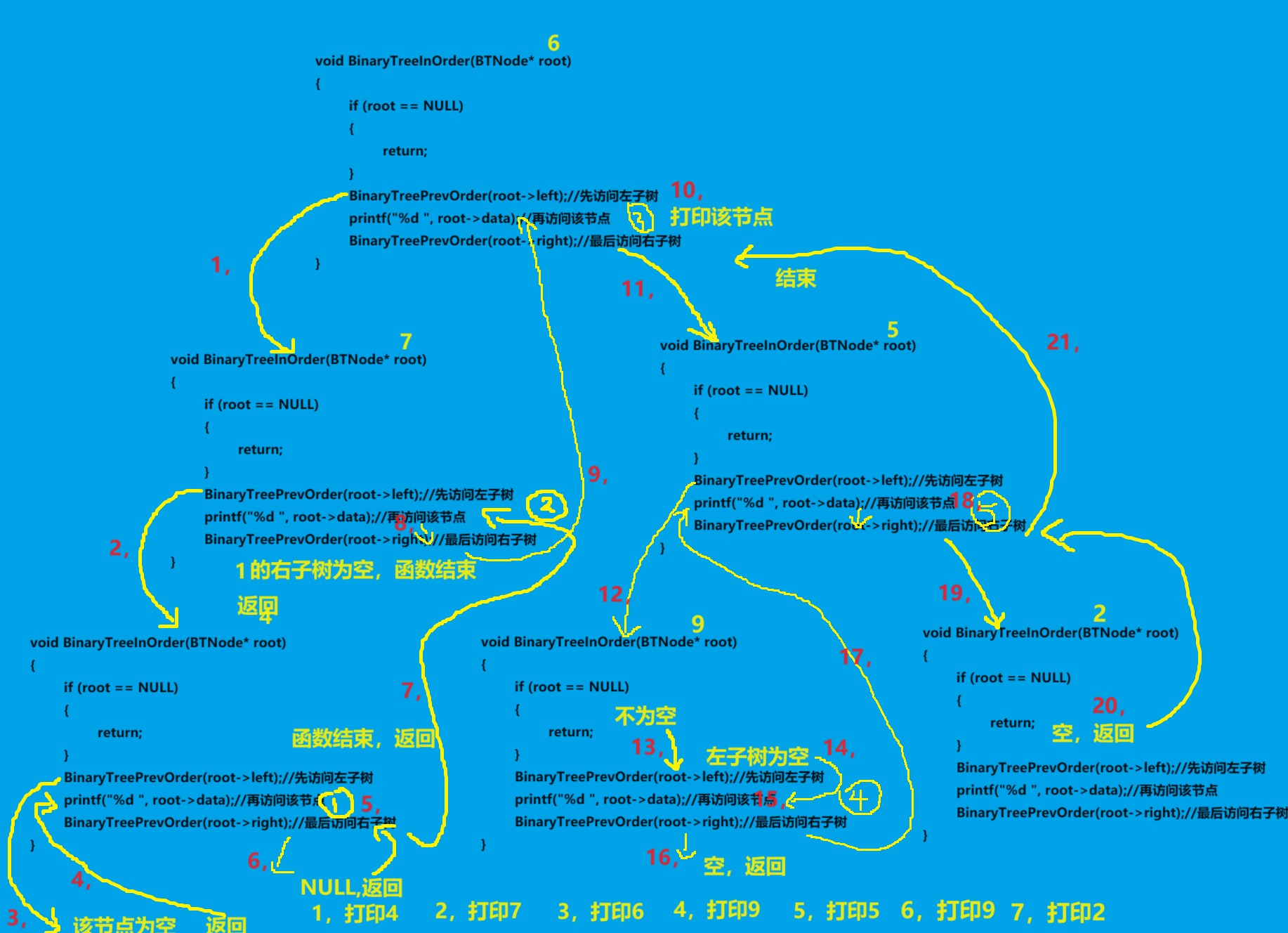
在这里插入图片描述

上边标注了步骤及打印顺序，遇到有关递归的题目，有不懂的地方只要画一画递归展开图就会豁然开朗
同样，后序还是更改一下顺序，按照左右根的顺序来访问打印，如果想要更加清晰地建看出，可以访问空节点返回前打印一个*号。
后序代码如下

//后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("*");
		return;
	}
	BinaryTreePrevOrder(root->left);//先访问左子树和右子树
	BinaryTreePrevOrder(root->right);
	printf("%d ", root->data);//最后访问该节点
}

二叉树全局遍历问题

树的节点个数

要找树的节点个数，分析，访问全树，如果为空树就返回，如果不是空树就加一。可以找一个变量来存储这个值，但由于局部变量在一个函数是单个个体，全局变量的安全性不高，我们可以传过来一个指针变量，每当访问到非空节点就解引用加一，空节点就return。
也可以利用返回值
代码如下

//树的节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
	//return root==NULL?0:BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;//三目操作符,前序
}

控制每个函数返回一个值，最后总和起来的就是节点的个数。归的条件是节点为空，返回的是统计的节点个数。

仍然利用上图讲解
在这里插入图片描述
递归展开图如下

到了这里，你是否已经开始熟悉递归的思路了。
相同类型的题目，不过要判断条件

叶子节点的个数

叶子节点就是数的枝叶，最末端节点，没有子节点的节点，结合上图来说就是4，9，2节点
递归函数我们要清楚自己的要求，当遇到满足条件时响应对应的变化，也要确定好归的条件。

叶子节点没有子节点，即这个节点的left和right都为空，和上边求节点个数类似，遍历整棵树，满足条件再++。
代码如下

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->right && root->left == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->right) + BinaryTreeLeafSize(root->left);
}

当遇到叶子节点就没必要继续向下找了，有些节点只有一个节点，还是不满足左右都为NULL，但是还是会遍历他的为空的节点，所以root==NULL为空，还是要返回。

第k层节点个数

这个时候就要考验条件筛选能力了，要找第K层节点个数，第一个思路就是直接递归找到第k层后，判断是否为空，如果不为空就使返回值++，在上层遍历时如果没有到第K层就遇到了空就返回。
也可以这样，找到第k-1层，判断该层的子节点数。怎么计算都可以，两种方法差别不大
第一种写法代码如下。

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

先断言一下层数是否错误。思路和前边介绍大致相同，只不过转化为了代码逻辑。一定要注意我们要实现什么功能，从而对症下药。

查找某值并返回

查找值为x的节点

上边的题都是遍历后返回总和，返回的数在每次递归中变化，现在要返回的是一个节点，如果查找到节点后返回，然后再递归的话，每个函数有不同的返回值，就会可能会改变我们最终想要的结果。
通过控制递归的返回值，接受判断，如果已经找到了就不再递归下去，直接将结果归回起始的函数，就可以完成任务。
代码如下

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* ret = NULL;
	ret=BinaryTreeFind(root->left, x);
	if (ret != NULL)
	{
		return ret;
	}
	ret = BinaryTreeFind(root->right, x);
	if (ret != NULL)
	{
		return ret;
	}
	return NULL;
}

返回值要在每个函数里判断一下，当然如果根节点的data就是x的话就直接返回该节点，如果不是就递归到左节点，如果左节点找到后会返回到调用的地方，然后会判断查找的结果是否为NULL，为空再继续调用右边的。
这道题有必要画一下递归展开图
还是以上边的图为例哈
假设查找节点值为9的节点
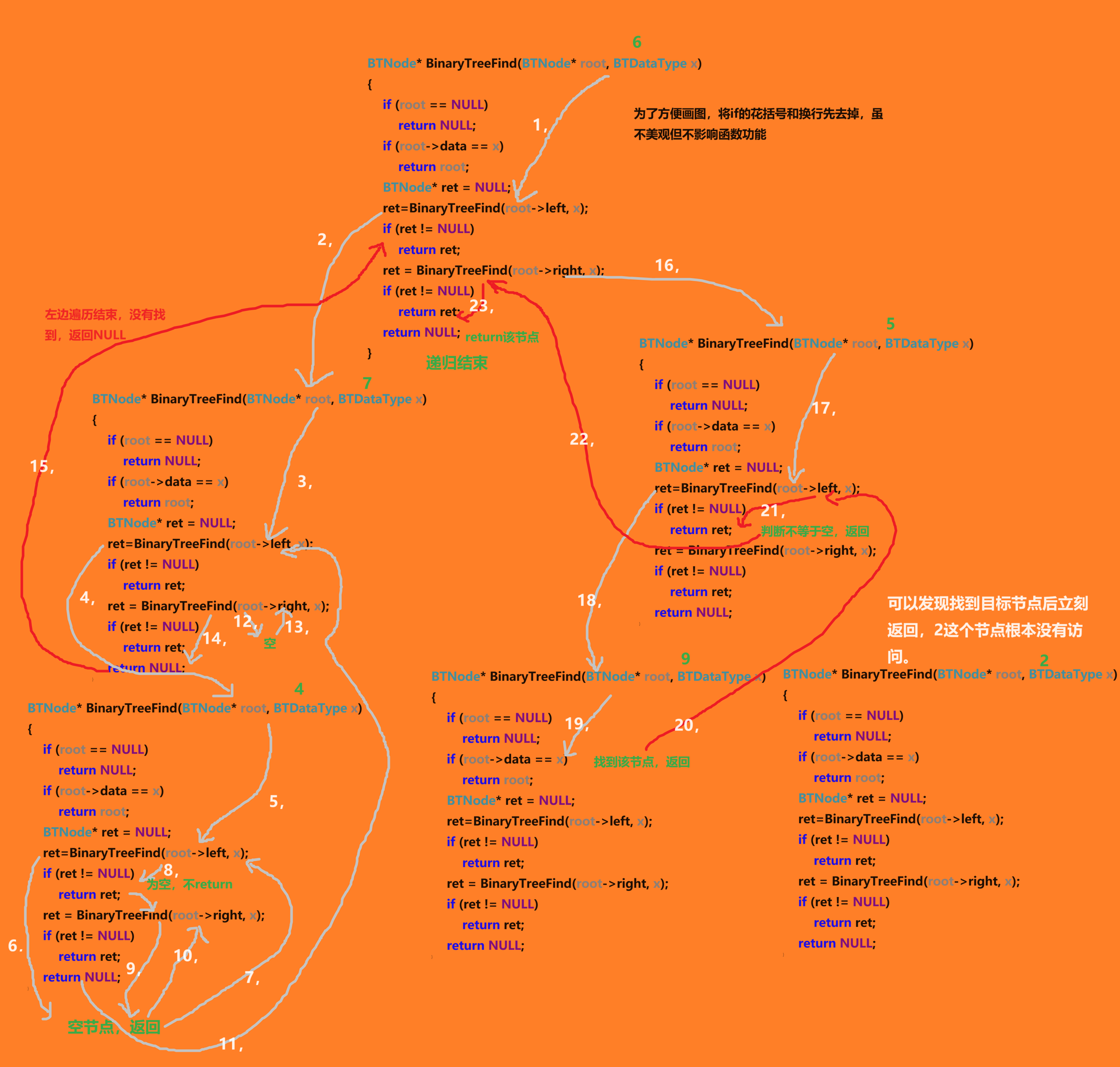
在这里插入图片描述
序号步骤十分清晰，这种递归十分巧妙，检查返回值，使所找节点直线返回。

判断树的结点的值相关问题

单值二叉树

Leetcode:单值二叉树
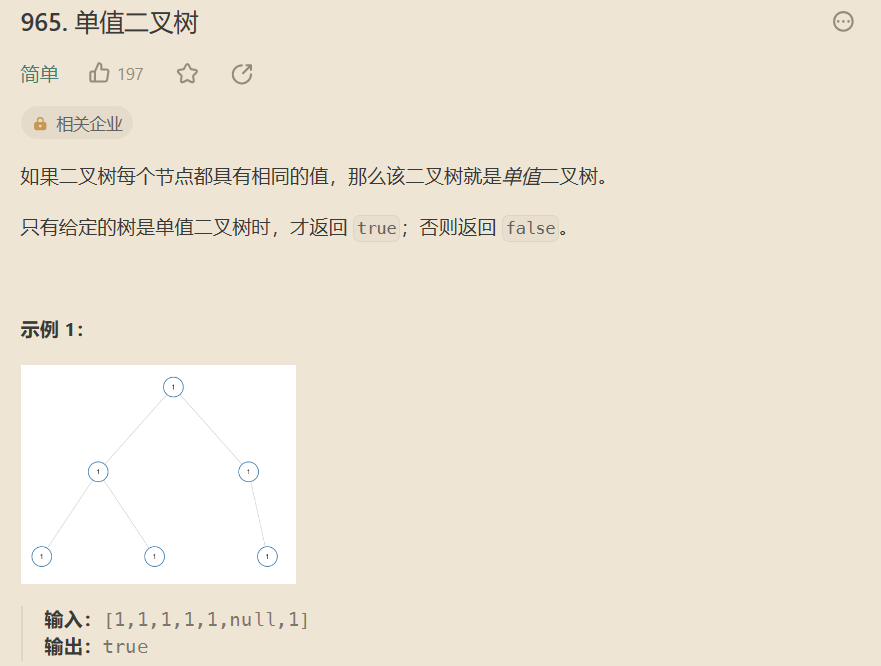
在这里插入图片描述
判断二叉树节点的所有值是否相同。
遍历全部节点，如果有一个树节点的左右子节点的储存的值与根节点不同，那么就返回false，遇到空节点就返回true，因为并不矛盾单值二叉树。
代码如下

bool isUnivalTree(struct TreeNode* root){
    if(root==NULL)
    {
        return true;
    }
   if(root->left&&root->left->val!=root->val)
    {
         return false;
     }
    if(root->right&&root->right->val!=root->val)
     {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

遍历所有节点，除非遇到空返回，遇到节点值与根节点不同的就返回false，最后返回左树和右树返回值的并且，只有两个皆为真，返回true，如果其中一个为假，就返回false，还有一个值得提出的就是，如果左树就找到false，就不会访问右树了，因为&&的前一个判断条件如果为假，就直接返回假，右树不会再遍历。

相同的树

Leetcode:相同的树
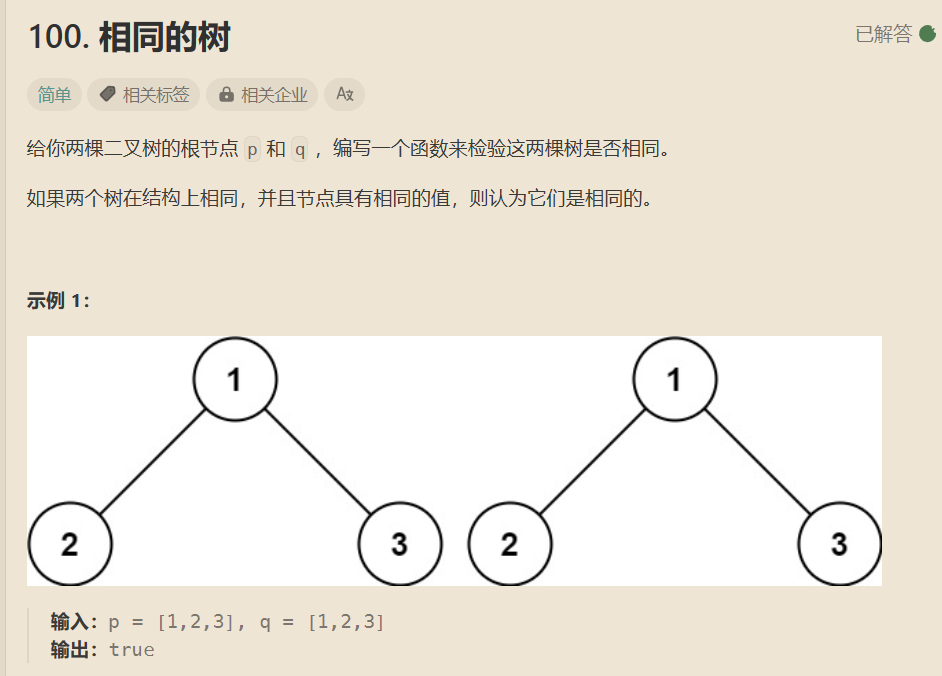
在这里插入图片描述
给定两个树，判断其保存的值是否相等。
先看根节点，再判断两树的左节点，右节点，如果有两个节点不相等就返回false，如果两个树都为空返回true，两个节点不相等返回false，相等就继续向下遍历。
思路清晰明了了
代码如下

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->right,q->right)&&isSameTree(p->left,q->left);
}

&&判断返回结果，上边已经介绍过了他的功能和强大之处，这里就不再赘述了。

数的结构的问题

这种类型的题目和前边的有一点不同，前边的不是做出判断就是获取节点的值，或者是统计数目，这种类型的题目是明确树的结构，想要做什么，实现什么操作，将树更改为题目要求的样子。

翻转二叉树

Leetcode:翻转二叉树
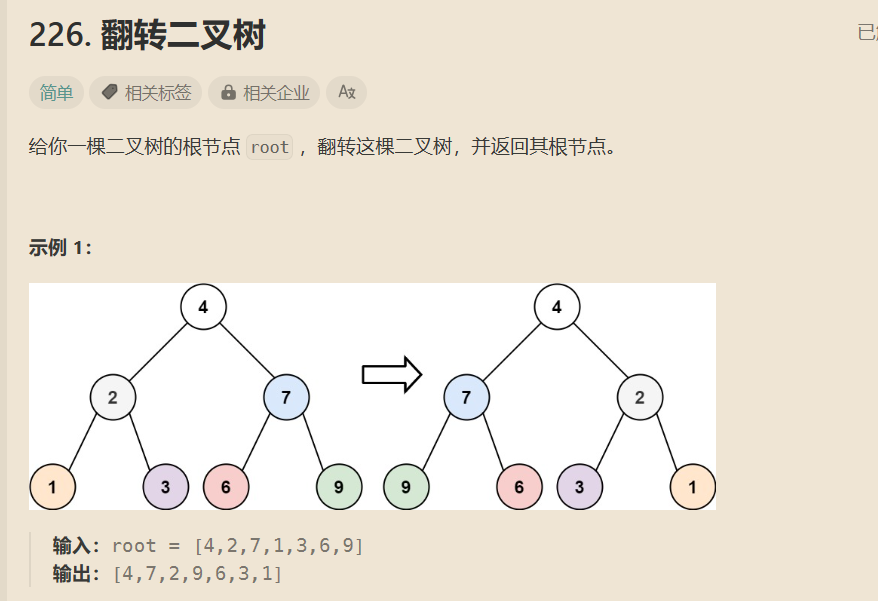
在这里插入图片描述
每个节点的左右节点都要反转，从根节点开始，把所有非空子节点的左右节点都换位，保存其左右节点，然后互换，两个都为空，换一换也无所谓，其中一个节点不为空，另一个节点为空，交换。
代码如下

struct TreeNode* invertTree(struct TreeNode* root){
    if(root==NULL)
    {
        return NULL;
    }
    struct TreeNode*left=invertTree(root->left);
    struct TreeNode*right=invertTree(root->right);
    root->left=right;
    root->right=left;
    return root;
}

对称二叉树

Leetcode:对称二叉树
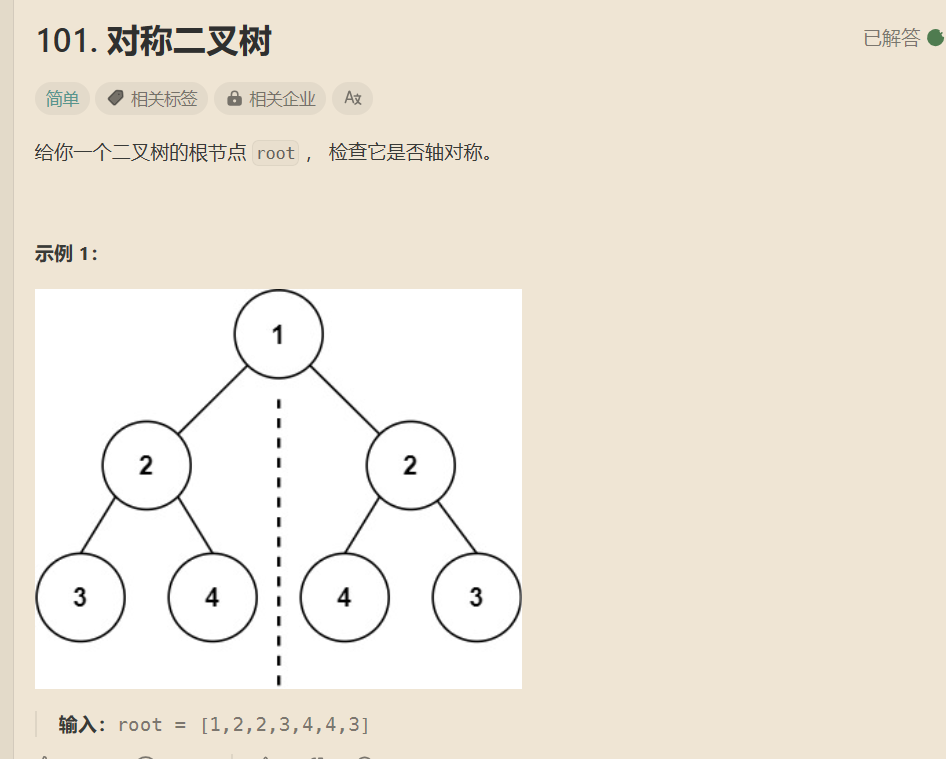
在这里插入图片描述
检查一个树是否为对称二叉树。

是b是感觉无从下手啊
这道题其实用前边的函数就可以实现。
相同的树以及翻转二叉树
将根节点的左子树翻转，再与右子树判断是否为相同的树。
代码如下

 struct TreeNode* invertTree(struct TreeNode* root){
    if(root==NULL)
    {
        return NULL;
    }
    struct TreeNode*left=invertTree(root->left);
    struct TreeNode*right=invertTree(root->right);
    //都找到了叶子节点
    // struct TreeNode*tmp=left;
    // left=right;
    // right=tmp;
    root->left=right;
    root->right=left;
    return root;
}
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->right,q->right)&&isSameTree(p->left,q->left);
}
bool isSymmetric(struct TreeNode* root){
    struct TreeNode*head=invertTree(root->right);
    return isSameTree(head,root->left);
}