Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题  --  同时算法要求图中所有边的权重非负（这个很重要）

针对一个带权有向图G ， 将所有节点分为两组S和Q ， S是已经确定的最短路径的节点集合，在初始时为空（初始时就可以将源节点s放入，毕竟源节点到自己的代价是0 ）， Q为其余未确定最短路径的节点集合，每次从Q中找出一个起点到该节点代价最小的节点u，将u从Q中移除，并放入S中，对u每一个相邻节点v进行松弛操作。松弛即对每一个相邻节点v，判断源节点s到节点u的代价与u到v的代价之和是否比原来的s到v的代价更小，若代价比原来小则要将s到v代价更新为s到u与u到v的代价之后，否则维持原样，如此反复，直到Q集合

贪心策略：每次去选从s->Q  去选最短路径边的那个顶点，去更新其连接的路径

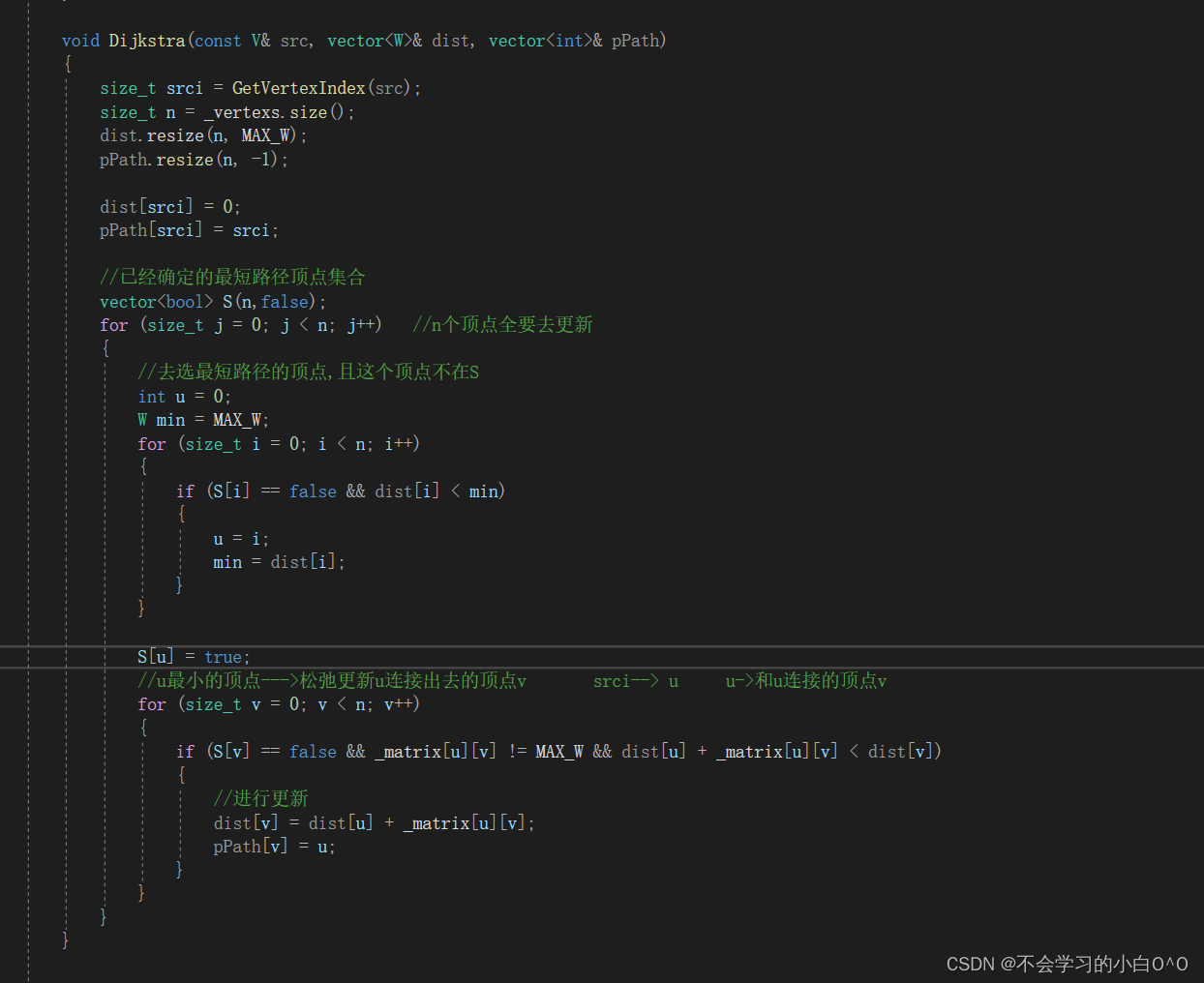
代码实现

Dijstra算法的缺陷

带有负权路的，搞不定