本文通过整理李宏毅老师的机器学习教程的内容，介绍神经网络中用于更新参数的反向传播法（backpropagation）的基本原理。

反向传播 backpropagation, 李宏毅

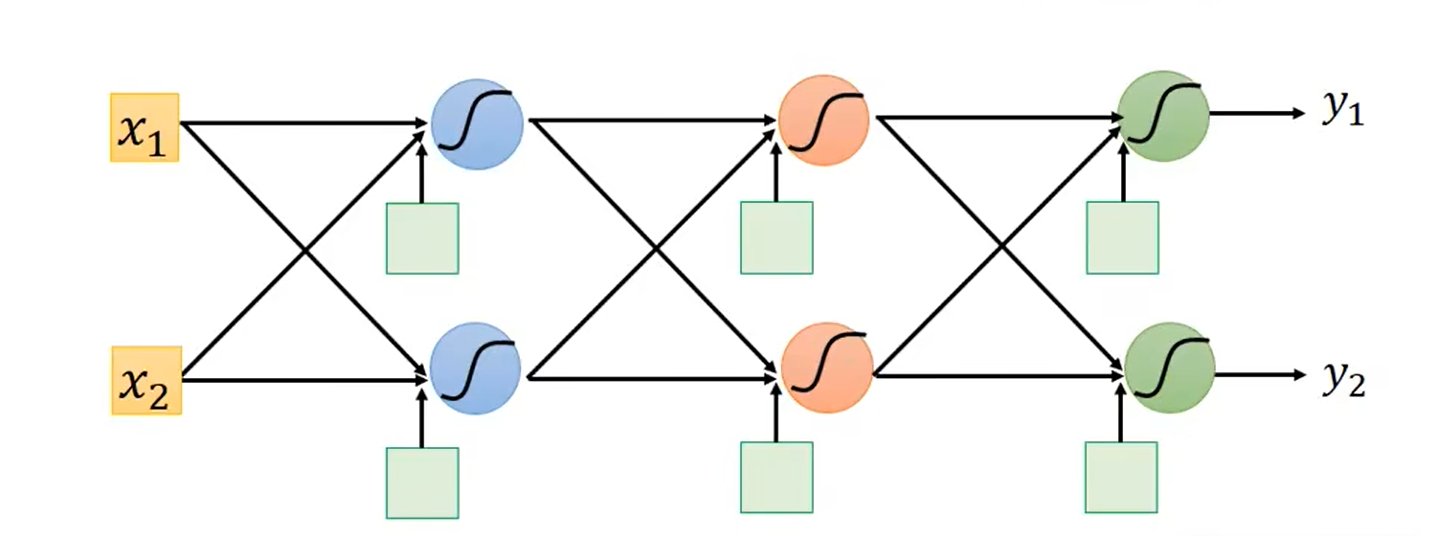
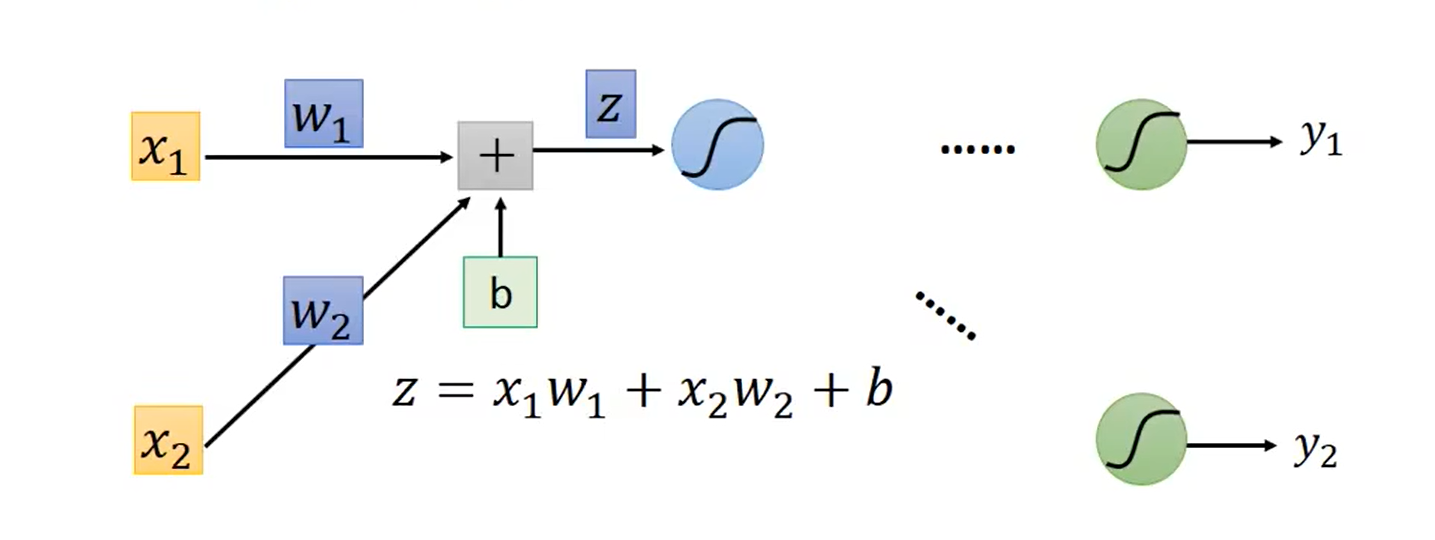
神经网络的结构：

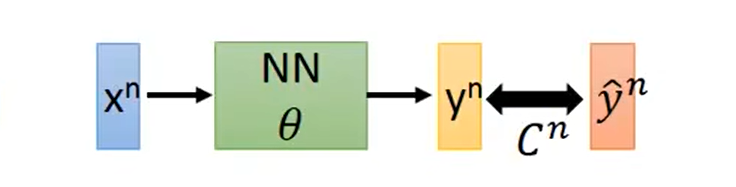
loss（损失）的计算：

$$L(\theta )=\sum _{n=1}^N{C}^n(\theta )$$

其中，上标 $n$ 表示第 $n$ 条数据。

易知：网络参数的更新取决于数据的 loss 值，而更新方式即为梯度下降法（gradient descent）。

以单个神经元为例：

loss 对参数 $w$ 的偏微分：
$$\frac{\partial L(\theta )}{\partial w}=\sum _{n=1}^N\frac{\partial C^n(\theta )}{\partial w}$$

对参数 $b$ 的偏微分类似。

简单地，考虑其中一条数据的 loss 值，并将 $C^n(\theta )$ 简记为 $C$，则：
$$\frac{\partial C}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial C}{\partial z}$$

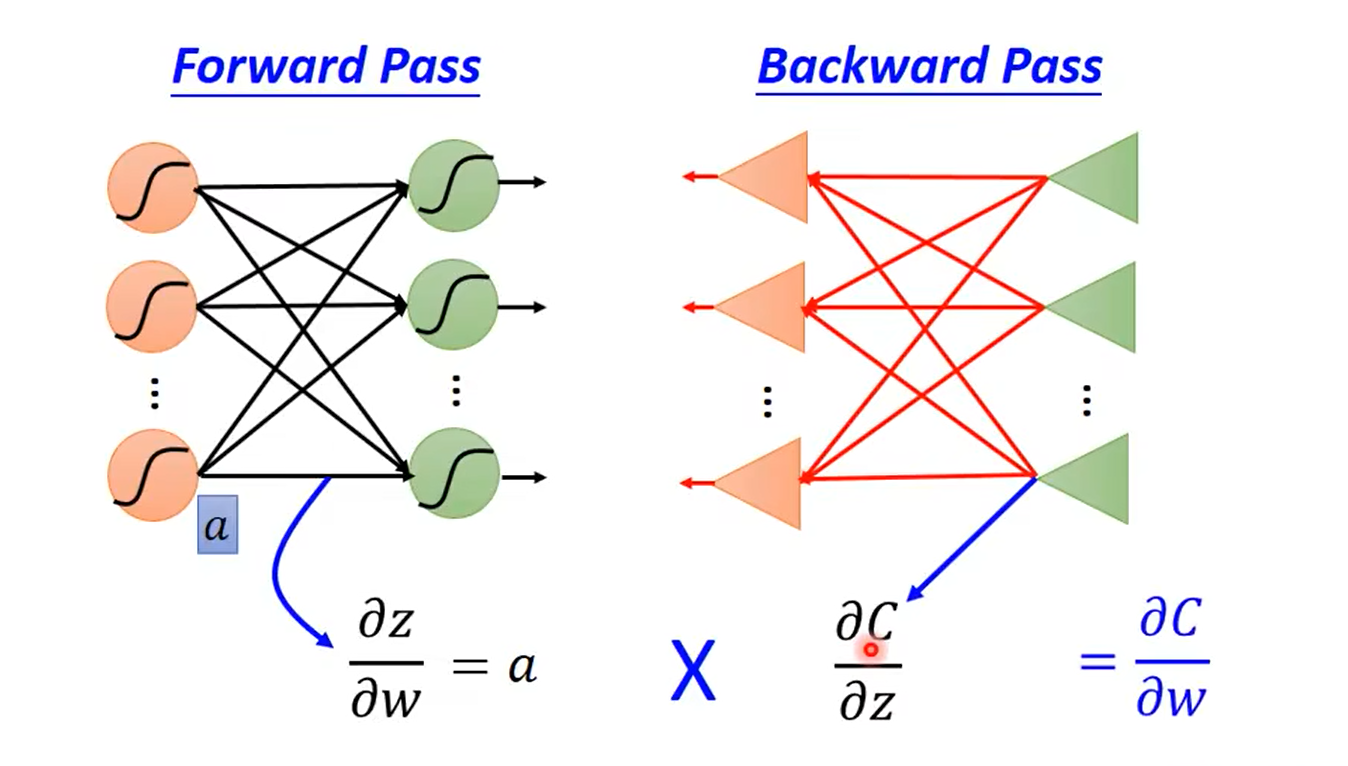
其中，对第一项偏微分 $\frac{\partial z}{\partial w}$ 的计算称为 forward pass，对第二项偏微分 $\frac{\partial C}{\partial z}$ 的计算称为 backward pass，继续看下去会理解其原因。

易知：第一项偏微分其实就等于数据输入 $x$，即：
$$\frac{\partial z}{\partial w_1}=x_1\frac{\partial z}{\partial w_2}=x_2$$

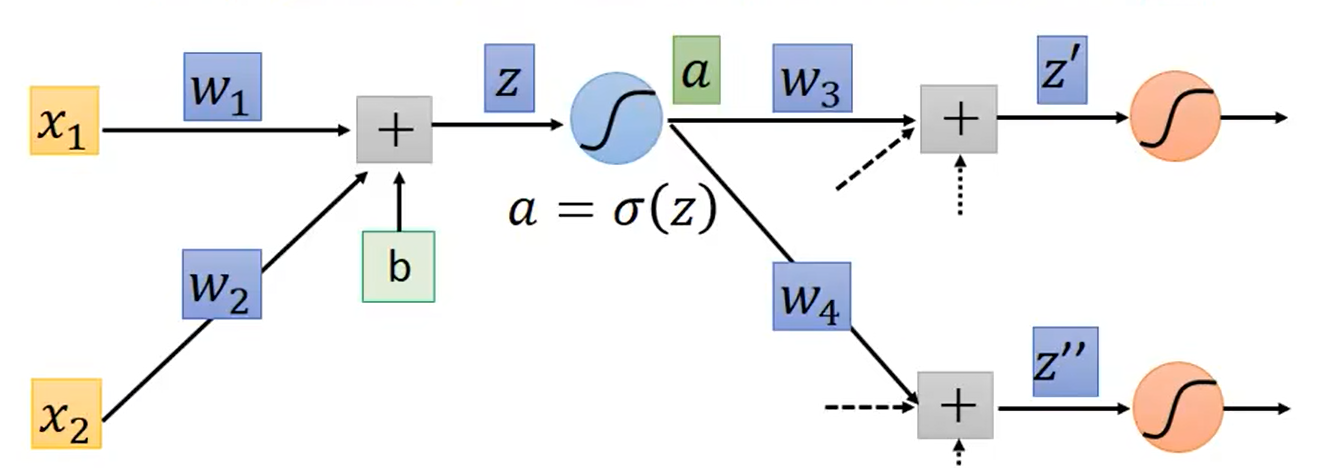
而计算第二项偏微分则不太容易，因为在 $z$ 后面的非线性模块之后，可能还有多个网络层：

于是对第二项偏微分 $\frac{\partial C}{\partial z}$ 继续展开，得到：
$$\frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a}$$

而由于非线性模块的输出 $a=\sigma (z)$，故第一项： $\frac{\partial a}{\partial z}={\sigma }^{\prime }(z)$；
而第二项可进一步展开为：
$$\frac{\partial C}{\partial a}=\frac{\partial z^{\prime }}{\partial a}\frac{\partial C}{\partial z^{\prime }}+\frac{\partial z^{\prime \prime }}{\partial a}\frac{\partial C}{\partial z^{\prime \prime }}$$

与前面类似地，有：
$$\frac{\partial z^{\prime }}{\partial a}=w_3\frac{\partial z^{\prime \prime }}{\partial a}=w_4$$

而计算 $\frac{\partial C}{\partial z^{\prime }}$ 和 $\frac{\partial C}{\partial z^{\prime \prime }}$ 需要下一次迭代，以此类推。

因此，如果网络的层级特别多，正向计算会非常繁琐。

但如果反过来看，从输出层开始，先得到 $\frac{\partial C}{\partial z^{\prime }}$ 和 $\frac{\partial C}{\partial z^{\prime \prime }}$，再反向计算前面各层的 $\frac{\partial C}{\partial z}$ 就会比较容易：

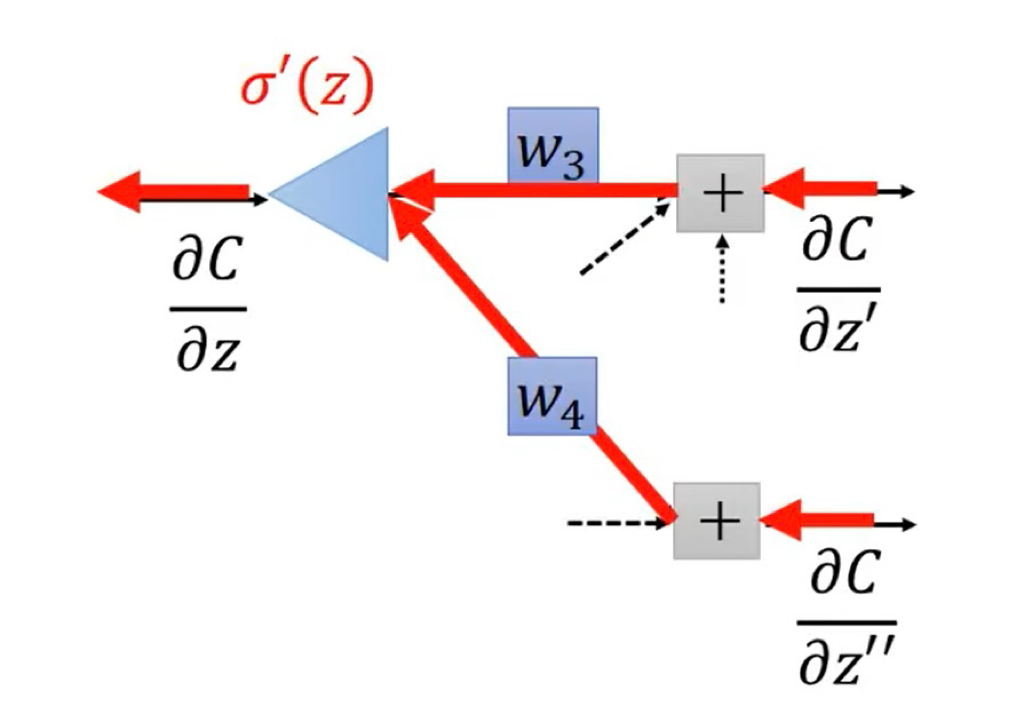
其中，由于正向计算时已计算过各层的输出，因此 ${\sigma }^{\prime }(z)$ 为常数。

最后，总结整体过程入下：