阅读时间:2023-10-24
1 介绍
年份:2016
作者:James Kirkpatrick, Razvan Pascanu, Neil Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A. Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka Grabska-Barwinska, Demis Hassabis, Claudia Clopath, Dharshan Kumaran, Raia Hadsell,加州史丹佛大學史丹佛大學
期刊:Proceedings of the national academy of sciences
引用量:5449
这篇论文的主题是关于神经网络如何克服灾难性遗忘的问题,灾难性遗忘是神经网络在顺序学习任务时的一个限制。论文提出了一种称为弹性权重合并(EWC)的方法,可以使神经网络在学习新任务的同时记住旧任务。EWC会有选择地降低对先前学习任务重要的权重的学习速度,从而防止灾难性遗忘。作者通过在MNIST数据集上解决分类任务和顺序学习Atari 2600游戏的实验来证明EWC的有效性。论文将EWC与其他方法如L2正则化和dropout正则化进行了比较,结果表明EWC在保持旧任务高性能的同时学习新任务方面优于这些方法。论文解释了EWC的实现和合理性,包括如何约束重要参数和确定哪些权重对于每个任务是重要的。论文还讨论了哺乳动物大脑可能支持无灾难遗忘连续学习的神经机制。总的来说,这篇论文通过使用EWC提出了解决神经网络灾难性遗忘问题的方法。
2 创新点
- EWC方法:论文提出了一种名为弹性权重整合的算法,用于实现神经网络的连续学习。该算法根据先前学习任务中权重的重要性,减缓学习过程,从而保留旧任务的知识。
- 在MNIST数据集和Atari 2600游戏中的应用:论文通过在MNIST数据集上进行分类任务和在Atari 2600游戏中进行学习来展示EWC的有效性。结果表明,相比于L2正则化和dropout正则化等其他方法,EWC在学习新任务的同时能够维持旧任务的高性能。
- EWC的实施和正当性:论文解释了EWC的具体实施和合理性,包括对重要参数的约束和确定每个任务中哪些权重是重要的。论文还提到了哺乳动物大脑中支持连续学习而不发生灾难性遗忘的神经机制。
3 算法
(1)计算步骤
- 计算每个权重在先前任务中的重要性:
- 先前任务的损失函数:L_prev(θ),其中θ表示网络的权重。
- Fisher信息矩阵:F_prev(θ) = E[∇²L_prev(θ)],其中∇²表示梯度的二阶导数。
- 权重重要性:I_prev(θ) = F_prev(θ) * (θ - θ_prev)²,其中θ_prev表示在先前任务上训练后的权重。
- 计算当前任务的损失函数:当前任务的损失函数:L_curr(θ)。
- 计算正则化项并更新网络权重:
- 正则化项:EWC_loss(θ) = L_curr(θ) + λ * Σ[I_prev(θ)], 其中λ是正则化项的权重,Σ表示对所有权重求和。
- 更新网络权重:θ_new = argmin(θ)[EWC_loss(θ)]
(2)推理过程
训练了一个模型,其参数为
θ
\theta
θ,定义最小化以下损失函数来完成此操作:
L
(
θ
)
=
L
n
e
w
(
θ
)
+
∑
i
=
1
n
λ
2
F
i
(
θ
i
−
θ
i
∗
)
2
\mathcal{L}(\theta) = \mathcal{L}_{new}(\theta) + \sum_{i=1}^{n} \frac{\lambda}{2} F_i (\theta_i - \theta_i^*)^2
L(θ)=Lnew(θ)+∑i=1n2λFi(θi−θi∗)2
其中,
L
n
e
w
(
θ
)
\mathcal{L}_{new}(\theta)
Lnew(θ) 是新任务的损失函数,n 是先前任务的数量,
F
i
F_i
Fi 是 Fisher 信息矩阵的对角线元素,
θ
i
∗
\theta_i^*
θi∗ 是在先前任务i中找到的最优参数。
λ
\lambda
λ 是一个超参数,控制先前任务对新任务的影响。
Fisher 信息矩阵是 Hessian 矩阵的期望值,它衡量了损失函数对参数的二阶导数。 在 EWC 中,只计算对角线元素,因为它们提供了最大的信息,同时也更容易计算。Fisher 信息矩阵的对角线元素可以通过以下公式计算:
F
i
,
j
=
E
x
∼
D
i
[
∂
log
p
(
y
∣
x
,
θ
)
∂
θ
i
∂
log
p
(
y
∣
x
,
θ
)
∂
θ
j
]
F_{i,j} = \mathbb{E}_{x\sim D_i}[\frac{\partial \log p(y|x,\theta)}{\partial \theta_i} \frac{\partial \log p(y|x,\theta)}{\partial \theta_j}]
Fi,j=Ex∼Di[∂θi∂logp(y∣x,θ)∂θj∂logp(y∣x,θ)]
其中,
D
i
D_i
Di是先前任务i的数据分布,
p
(
y
∣
x
,
θ
)
p(y|x,\theta)
p(y∣x,θ)是模型在给定输入x 和参数
θ
\theta
θ的情况下预测输出y的概率分布。
在每次学习新任务之前,需要计算 Fisher 信息矩阵和最优参数
θ
i
∗
\theta_i^*
θi∗。这可以通过在先前任务上运行梯度下降来实现,直到收敛为止。一旦计算出 Fisher 信息矩阵和最优参数,就可以使用 EWC 来学习新任务,同时保留先前任务的知识。
最后,可以使用以下公式计算 EWC 梯度:
g
i
=
∇
θ
i
L
n
e
w
(
θ
)
+
λ
∑
j
=
1
n
F
i
,
j
(
θ
i
−
θ
i
∗
)
g_i = \nabla_{\theta_i} \mathcal{L}_{new}(\theta) + \lambda \sum_{j=1}^{n} F_{i,j} (\theta_i - \theta_i^*)
gi=∇θiLnew(θ)+λj=1∑nFi,j(θi−θi∗)
其中,
g
i
g_i
gi是 EWC 梯度,
∇
θ
i
L
n
e
w
(
θ
)
\nabla_{\theta_i} \mathcal{L}_{new}(\theta)
∇θiLnew(θ)是新任务的梯度。通过添加正则化项,EWC 可以确保新任务不会完全覆盖先前任务的知识,从而在连续学习中实现知识共享。
5 实验结果分析
(1)总结一
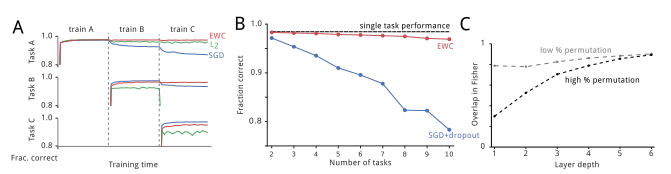
- 使用纯随机梯度下降(SGD)训练这个任务序列会引发灾难性遗忘。
- 图2A展示了两个不同任务的测试集性能。在训练从第一个任务切换到第二个任务时,任务B的性能迅速下降,而任务A的性能迅速上升。
- 任务A的遗忘问题会随着更长的训练时间而进一步恶化。
- 使用L2正则化不能解决这个问题,因为它对所有权重施加了相同的保护限制,导致在任务B上学习的能力受到限制。
- 然而,使用EWC可以根据任务A中每个权重的重要性,使网络能够在不遗忘任务A的情况下很好地学习任务B。
- 图2B展示了使用EWC和使用SGD与dropout正则化的所有任务的平均性能。可以看到EWC在旧任务上保持了高性能,并且仍然能够学习新任务。
- 图2C展示了两个不同置换程度下网络深度的Fisher信息矩阵的相似性。任务越不相似,早期层的Fisher信息矩阵重叠越小。
(2)总结二
- 当网络在两个非常相似的任务上训练(两个MNIST版本,只有少数像素被重排),这两个任务在整个网络中依赖于相似的权重集
- 当两个任务之间更不相似时,网络开始为两个任务分配单独的能力(即权重)。
在进行大量重排时,网络靠近输出的层确实被两个任务重复使用。这反映了重排使得输入对内容是非常不同的,但输出的内容(即类别标签)是共享的。
(3)总结三
EWC可以在要求更高的强化学习(RL)领域中支持连续学习。作者测试了在经典的Atari 2600游戏集上,将Deep Q Networks与EWC相结合的方法。实验中,通过使用EWC,能够学习多个游戏,而不会忘记以前学习的游戏 。与以前的RL方法相比,EWC利用了固定资源(即网络容量)的单个网络,并且计算开销较小。
6 代码
https://github.com/yashkant/Elastic-Weight-Consolidation