1. 论文概要

论文下载地址：ECO: Efficient Convolution Operators for Tracking
发表时间：CVPR 2017
作者：Martin Danelljan（瑞典），目标跟踪领域的大牛
官方代码：https://http://github.com/martin-danelljan/ECO

ECO 算法具有高效卷积特性，是一种以提高时间和空间效率为出发点的目标跟踪算法。

2. 研究背景和动机

视觉跟踪（visual tracking）的目标是在给定初始状态时，估计出图像序列中目标的运动轨迹。目标跟踪是实时的，一个理想的跟踪系统应该是实时和准确的。

近年来，许多效果较好的目标跟踪算法都是基于判别相关滤波器（Discriminative Correlation Filter, DCF）的。最早用到相关滤波的是2010年提出的的MOSSE，速度非常快。之后的KCF，DSST，CN，SRDCF，C-COT等都是在相关滤波的基础上做的。随着特征维度越来越高，算法越来越复杂，跟踪效果虽然是在逐步提升，但是都是以牺牲跟踪速度为代价的。

Martin Danelljan 在相关滤波做跟踪的算法上积累了丰富的经验之后，分析了速度降低的三个最重要的因素：

1. 模型大小（特征复杂度）：
   如C-COT用了CNN+HOG+CN这样非常全面的特征组合，它每次更新模型的时候，需要更新的参数有800000个，速度当然很慢。实际上跟踪问题中的训练样本非常少，这么高的维度除了速度慢，还会引起过拟合。

2. 训练集大小：
   这里所指的训练集是指保存了每一帧的跟踪结果的训练集，也就是说，每一次进行model update的时候，要用在这一帧之前所有跟踪到的样本。那么随着视频越来越长，这个训练集就会越来越大。那么一般的解决方案是保存比较新的样本，丢弃老的样本，具体策略每个方法都不一样。这样一来，模型还是容易过拟合。因为当目标被遮挡或者丢失的时候，比较新的这些样本本身就是错的，那么模型很容易有model drift，就是被背景或者错误的目标污染，导致跟踪结果出错。另外，样本集的保存也会使得空间效率低下，增加计算负担。

3. 模型更新方式：
   模型如果每帧都更新，速度肯定比间歇更新要慢。

为了解决上述三个问题，ECO分别提出了针对性的策略来提高跟踪器的效率。

参考：目标跟踪算法二：ECO: Efficient Convolution Operators for Tracking

3. 相关滤波用于目标跟踪的原理

跟踪算法整体上可分为两类：

• 生成式跟踪算法：
  首先对目标区域进行特征提取，然后进行模板匹配：基于特征进行目标模板与目标候选块之间的相似度匹配，最大相似度对应的候选块即为当前帧的目标。

• 判别式跟踪算法：
  将图像背景信息考虑到算法中，结合目标前景信息和背景信息训练一个判别函数，对目标和背景进行分类与相似度计算，从而实现目标的跟踪定位。

参考：相关滤波器（Correlation Filters）

两个信号越相似，相关性越高，即做相关运算后得到的相似值越大。
相关滤波跟踪的基本思想是模板匹配，设计一个滤波模板，利用该模板与目标候选区域做相关运算，最大输出响应的位置即为当前帧的目标位置。

相关运算的最大优势在于，它通过傅里叶变换将时域上的卷积运算变为频域上的乘积运算，即

        

相关滤波目标跟踪算法的主要流程为：

1. 初始化：在第一帧中，选择或检测一个目标区域并计算该区域的傅里叶变换。
2. 跟踪：对于后续的每一帧，计算当前帧中目标区域的傅里叶变换，然后计算当前帧与第一帧之间的互相关系数，得到一个响应图。
3. 位置估计：在响应图中找到最大值，即得到目标的位置估计。
4. 更新模板：在当前帧中重新选择目标区域，计算该区域的傅里叶变换，并进行一定程度的平滑处理，作为下一帧的模板。

相关滤波目标跟踪算法流程图：

        

4. ECO算法流程

ECO 算法流程图如下：

        

ECO 算法步骤为：

1. 初始化：在第一帧中，选择或检测一个目标区域
2. 特征提取：提取目标区域的梯度直方图特征 (histogram of oriented gradient, HOG) 或颜色通道特征(color names, CN)
3. 连续卷积：通过连续卷积算子将特征图从离散域转换到连续域得到融合的高维度特征
4. 特征降维：利用 PCA 对高维度特征进行降维，并将降维后的特征加入样本空间模型
5. 间隔帧更新参数：样本空间模型结合高斯牛顿法每隔 6 帧图片更新一次相关滤波器参数
6. 跟踪：将每次跟踪时经过处理的特征输入相关滤波器，得到相关响应图
7. 位置估计：将响应值最大的位置作为目标跟踪结果

5. ECO算法创新点

5.1 特征降维：PCA

ECO 的 Baseline 是 C-COT 算法，C-COT 算法采用插值方法将搜索区域的多分辨率特征 $x$ 进行如下式所示的运算转换到连续的空间域中：

        

式 (4-1) 可以看做特征提取过程，最后得到的特征是 J { x } J\{x\} J{x}

C-COT 算法计算响应得分的公式为：

        

样本 $x_j$ 的 labeled detection scores $y_j(t)$ 被设置为周期性重复的高斯函数，目标函数定义为加正则化项的 $L_2$ loss：

        

ECO 算法在 C-COT 算法的基础上，采用主成分分析法 (PCA) 进行特征降维。C-COT中对于每个特征通道都需要训练一个单独的滤波器，共有D个滤波器。ECO使用 PCA 选择其中 C (C<D) 个滤波器构造了一个 D*C 的投影矩阵 P，将特征降维为 P T J { x } P^TJ\{x\} PTJ{x}。计算新的响应得分为：

        

通过傅里叶变换转换到频域的训练相关滤波器的目标函数为：

        

其中 z = J { x } z=J\{x\} z=J{x}，(7)是一个非线性最小二乘问题，论文中把这个问题转化为一个矩阵的因式分解问题，用 Gauss-Newton 和 Conjugate Gradient 来求解。

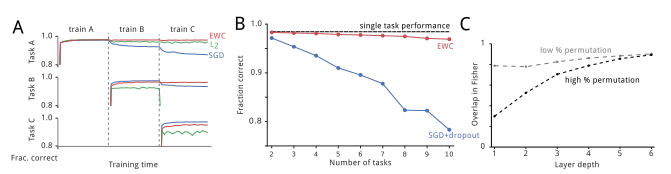
下图展示了从 C-COT 的 512 个滤波器中选择的 64 个能量较高的滤波器，其他大多数滤波器包含的能力可以忽略不计。

5.2 训练集简化：GMM

如下图所示，Baseline是传统的训练集，每更新一帧就加一个进来，那么连续的数帧后训练集里面的样本都是高度相似的，即容易遗忘前面的样本，且容易对最近的若干帧样本过拟合。

ECO用了高斯混合模型 (GMM) 来生成不同的分量 (component)，每一个 component 基本就对应一组比较相似的样本，不同的component之间有较大的差异性。这样就使得训练集具有了多样性。

        

通过样本 $x$ 和目标输出 $y$ 的联合概率分布 $p(x,y)$，将目标函数写为：

由于目标输出的 $y$ 的形状都是一致的，是一个峰值在目标中心的高斯函数，只是峰值位置不一样。ECO 将 $y$ 都设置成一样的，把峰值位置的平移量体现到 $x$ 上，在频域中可以简单处理。那么 $p(x,y)$ 就简化了，只需要计算 $p(x)$ 就行了。这里用 GMM 来建模：

        

其中 L 表示 Gaussian components 的数量。

GMM的更新过程为：

1. 对于一个新样本 $x_j$，使用 ${\pi }_m=\gamma$ 和 ${\mu }_m=x_j$ 初始化一个 component m
2. 如果 components 的数量大于L，则丢弃一个权重最小的 component；否则合并两个最近的 component $k$ 和 $l$ 为一个新的 component $n$：
   
   使用 Parseval 公式在傅里叶域中计算二者的距离 $||{\mu }_k-{\mu }_l||$
3. 计算目标函数：
   

使用 GMM 将原来的 $M$ 个样本减少为 $L$ 个 components 的平均值，实验中设置 $L=M/8$

5.3 模型更新策略：间歇更新

标准的基于 DCF 的跟踪方法是在每一帧中更新滤波器，但这样会导致速度较慢。

ECO 每隔 $N_s$ 帧更新一次参数，实验中设置 $N_s=6$ 。注意这里的Ns只是对模型的更新，样本的更新是每一帧都要做的。模型更新频率降低，当然节约了时间，并且可以避免模型的漂移问题，一定程度上改进效果，但是也不可以把Ns取得太大，否则会使得模型跟不上目标的变化。