10.25
求解马鞍点问题
若矩阵Anm中某个元素A[i][j]是矩阵第i行中值最小的元素，同时又是第j列中值最大的元素，则称元素A[i][j]是矩阵中的一个马鞍点。
设以二维数组存储矩阵，编写算法求矩阵A中的所有马鞍点，算法的时间复杂度要尽量的低。
注意当最大值（最小值）并列相等时，会出现多鞍点的情况。
输入格式 :
第一行输入矩阵的总行数M和总列数N，以空格间隔。
之后的M行，依次输入矩阵的各行数据，以空格间隔。
输出格式 :若有马鞍点，则以行序为主序，依次输出各个马鞍点。
每个马鞍点以（row, col, val）的形式输出，其中row 代表马鞍点的行号，col代表马鞍点的列号，val代表马鞍点的值。
若无马鞍点，则输出“NONE”。

#include <stdio.h>
#define Mmax 100
#define Nmax 100

int main()
{
	int M, N;
	int i, j, k, b = 0, min, t = 0;
	int A[Mmax][Nmax];
	int B[Nmax];

	scanf("%d %d", &M, &N);
	for (i = 0; i < M; i++)
	{
		for (j = 0; j < N; j++)
		{
			scanf("%d", &A[i][j]);
		}
	}
	for (i = 0; i < M; i++)
	{
		min = A[i][0];
		B[t] = 0;
		t++;
		for (j = 1; j < N; j++)
		{
			if (A[i][j] < min)
			{
				min = A[i][j];
				t = 0;
				B[t] = j;
				t++;
			}
			else if (A[i][j] == min)
			{
				B[t] = j;
				t++;
			}
		}
		for (k = 0; k < t; k++)
		{
			int y, l = 0;
			int x = B[k];
			for (y = 0; y < M; y++)
			{
				if (min < A[y][x])
				{
					l = 1;
				}
			}
			if (l == 0)
			{
				printf("(%d,%d,%d)", i + 1, x + 1, min);
				b = -1;
			}
		}
	}
	if (b != -1)
	{
		printf("NONE");
	}
}

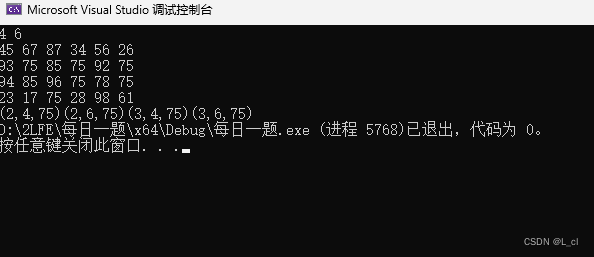
运行结果：