奥坎·耶尼贡
一、说明
对于存在隐含变量的模型,有卡尔曼、隐马尔可夫、混合高斯模型、EM算法,这些模型都是建立在一种理论,贝叶斯推断理论,本篇讲授典型的贝叶斯推断原理。
二、原理综述
贝叶斯优化是一种用于黑盒函数全局(最优)优化的技术。
黑匣子是观察者不知道其内部运作的系统。她只能访问系统的输入和输出,但不知道系统如何根据输入得出输出。在优化的背景下,黑盒函数指的是目标函数。

为了说明这一点,请考虑我们无法访问的函数f 。我们无法直接访问f或计算其梯度。我们唯一可用的信息是提供输入x并接收真实输出的噪声估计(或没有任何噪声)。

我们的目标是根据我们的目的优化黑盒函数f内的潜在价值,例如最大化它。
在传统的优化方法中,例如网格搜索或随机搜索,目标函数是在一组预定义的点处评估的。然而,在处理高维或噪声函数时,这些方法可能计算成本昂贵且效率低下。
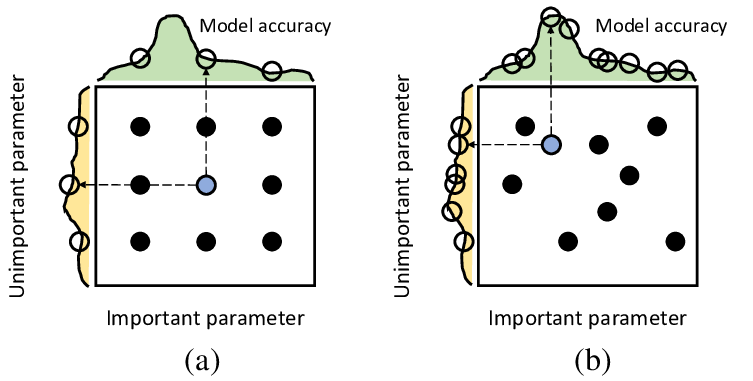
(a)网格搜索之间的比较;(b) 随机搜索超参数调整。来源
贝叶斯优化与传统方法相比具有多种优势。首先,它通过构建概率代理模型来有效处理昂贵且嘈杂的函数评估,该模型捕获不确定性并智能地指导搜索过程。
它结合了有关目标函数的先验知识或信念,从而能够做出更明智的决策。
它还平衡了探索和利用。探索允许对搜索空间进行更广泛的探索,有可能发现更好的解决方案,而利用则侧重于利用已知的有前途的领域来优化当前的最佳解决方案。平衡这两方面对于寻找更好的解决方案和完善最佳解决方案至关重要。
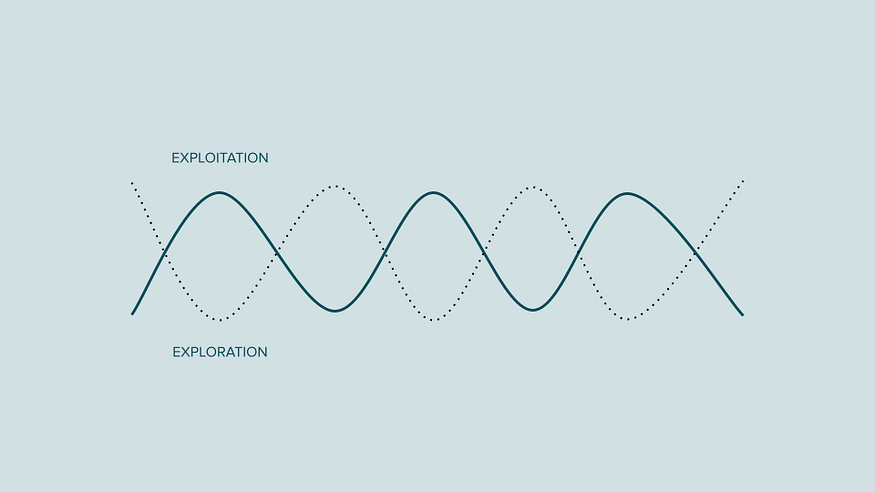
利用与探索。来源
经典老虎机算法利用频率界限来对未知函数进行建模。Bandit 问题是一类顺序决策问题,涉及在一系列步骤或时间段内从一组选项(臂)中选择操作。每个手臂都有一个与之相关的未知奖励分布,目标是通过策略性选择手臂来最大化获得的累积奖励。
在所描绘的立方体形状中,沿着三个轴表示三个指标,提供了在更广泛的层面上对心态变化的理解。
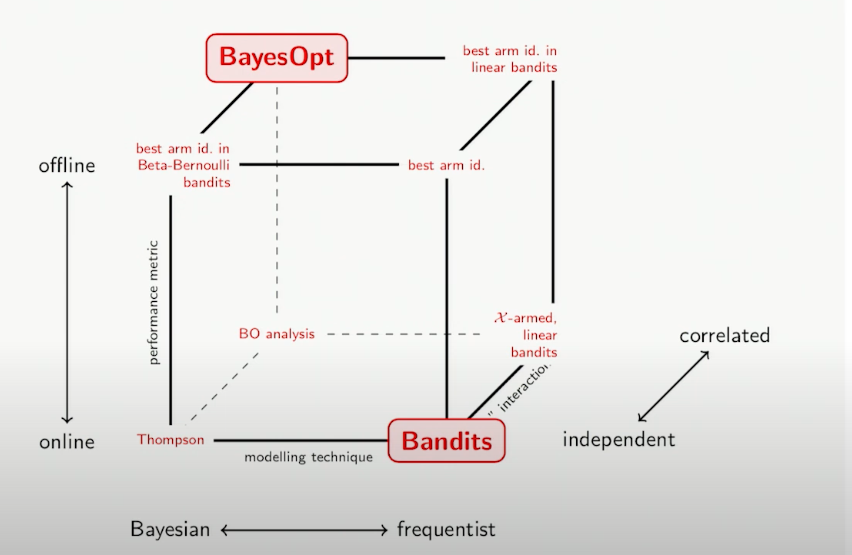
强盗 vs 贝叶斯。来源
绩效指标是关于后悔设置的。遗憾设置是一个用于分析和量化决策算法或策略在顺序决策问题中的性能的框架。它衡量所选政策的绩效与事后可能选择的最佳政策之间的累积差异。

后悔。来源
- 离线性能指标:离线性能指标使用事后信息评估算法或策略。它衡量如果算法从一开始就能够访问完整的数据集或信息,算法的执行效果如何。换句话说,它根据尽可能最好的事后知识来衡量绩效。
- 在线性能指标:另一方面,在线性能指标在更现实的场景中评估算法或策略,在该场景中,决策是使用有限的信息顺序做出的。它根据所做的实际决策及其结果来衡量绩效,而无需获取未来信息。在线性能指标反映了算法在动态和不确定环境中的真实性能。
立方体的 X 轴显示建模技术,可以是贝叶斯或频率论。在 Z 轴上,立方体表示变量之间的关系,特别是一个变量是否提供有关另一变量的信息或见解。
三、算法
给定:函数f(x), 我们想要最大化它。我们有一些f的数据。

步骤:
- 初始样本:首先随机选择一组有限的样本点。
- 初始化模型:利用这些点来计算代理函数。
- 迭代:
3.1. 获取函数:使用获取函数并获取下一个点。
3.2. 更新模型:重新评估代理函数。
3.3. 验证点:验证代理函数是否保持稳定,或者方差是否低于预定阈值,或者f是否已用尽,具体取决于您的具体设计目标。
四、给定函数
例如,让我们创建一个黑盒函数,它将正弦和余弦函数组合起来生成输出。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def black_box_function(x):
y = np.sin(x) + np.cos(2*x)
return y
# range of x values
x_range = np.linspace(-2*np.pi, 2*np.pi, 100)
# output for each x value
black_box_output = black_box_function(x_range)
# plot
plt.plot(x_range, black_box_output)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Black Box Function Output')
plt.show()x_range使用 计算每个 x 值 ( ) 的函数值black_box_function,然后绘制输出。
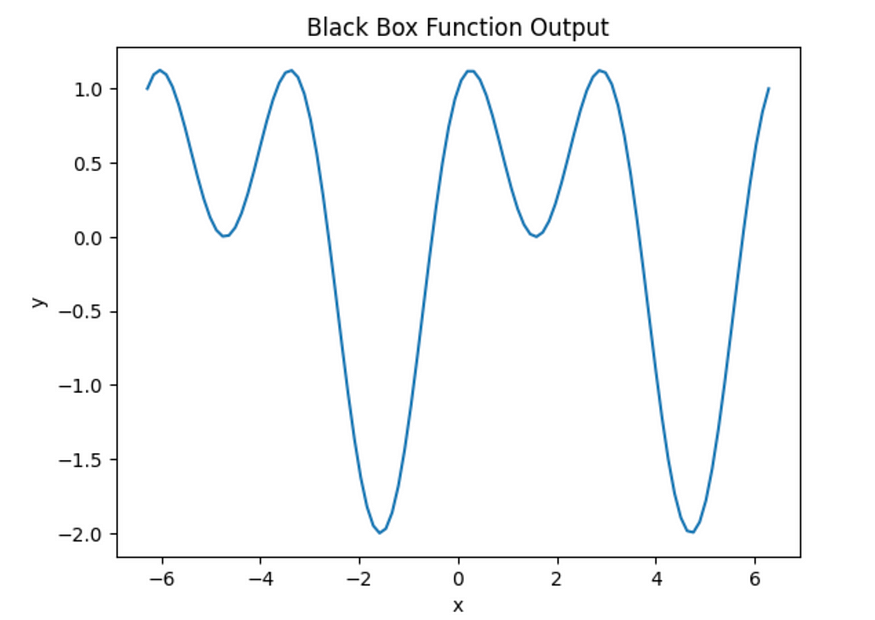
黑盒函数输出图。图片由作者提供。
五、初始样本
函数f的输出示例。
# random x values for sampling
num_samples = 10
sample_x = np.random.choice(x_range, size=num_samples)
# output for each sampled x value
sample_y = black_box_function(sample_x)
# plot
plt.plot(x_range, black_box_function(x_range), label='Black Box Function')
plt.scatter(sample_x, sample_y, color='red', label='Samples')
plt.xlabel('x')
plt.ylabel('Black Box Output')
plt.title('Sampled Points')
plt.legend()
plt.show()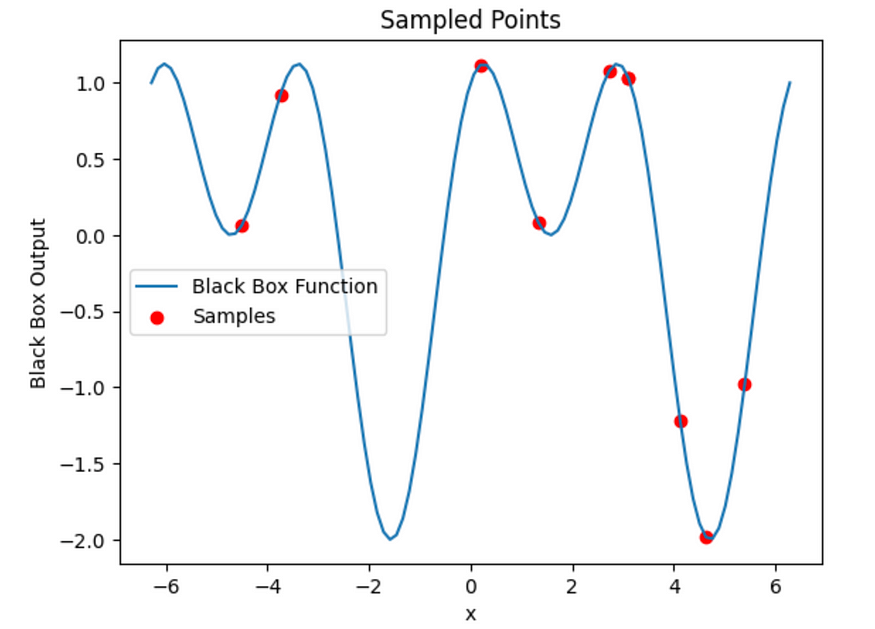
采样。图片由作者提供。
六、造型
贝叶斯优化中的代理模型充当真实目标函数的代理。它们捕获函数行为的不确定性,并提供搜索空间内未观察点处函数值的预测或估计。通过基于观察到的函数评估迭代更新代理模型,贝叶斯优化指导搜索可能包含最佳解决方案的搜索空间区域。
我们的目标是开发一个模型,表示为M,它不仅能够提供预测,还能够保留与这些预测相关的不确定性度量。为此,我们将采用以下预定义接口:
- 观察(M,x,y):记录观察结果->全部
- 预测( M, x ): 进行后验预测 -> 全部
- 样本(M,x):样本潜在函数值 - > Thompson
- getTail( M, v, x ):超过x -> PI的概率
- getImprovement( M, v, x ): v -> EI上面的积分
- getQuantile( M, q, x ):第q个分位数 -> UCB
- getEntropy( M, x ): 预测熵 -> P(ES)
执行各种过程的能力指示了可以在模型类中使用的方法和采集功能的类型。前两者适用于所有贝叶斯优化模型。此外,例如,如果您可以访问尾部概率,则可以利用改进概率 (PI) 方法。
七、高斯过程
高斯过程 (GP) 通常用作贝叶斯优化中的代理模型。高斯过程定义了函数的分布,其中任何有限的函数值集都遵循多元高斯分布。在贝叶斯优化的背景下,GP 用于对未知目标函数进行建模,并提供给定观测数据的函数值的后验分布。
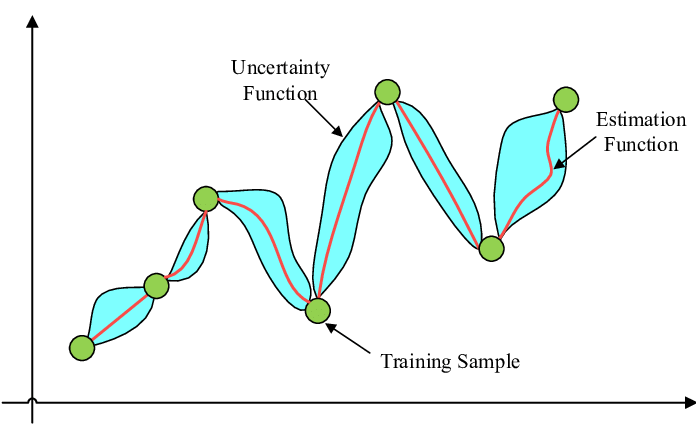
高斯过程由估计函数和不确定性函数指定。来源
GP 完全由其均值函数和协方差函数(也称为核函数)指定。均值函数表示函数在每个输入点的期望值,而协方差函数则表征不同输入点之间的关系并控制生成函数的平滑度和行为。
给定一组观测数据,GP 可用于预测未观测点的函数值。这些预测基于观测数据以及均值和协方差函数中编码的基本假设。重要的是,GP 提供了与这些预测相关的不确定性度量,允许对预测中的不确定性进行有原则的处理。
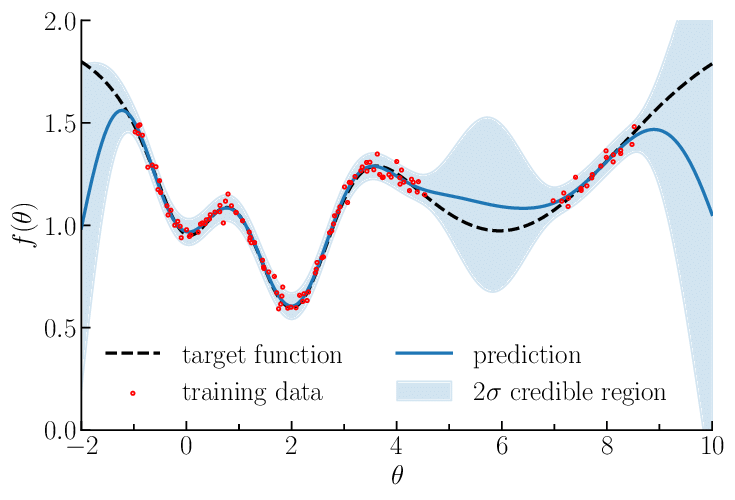
一维高斯过程回归的图示。来源
在先验知识有限的领域中,高斯过程特别有用,因为它们依赖于相似输入导致相似输出的假设。这使得高斯过程非常适合在没有太多先验信息的情况下检测数据中的模式和趋势。
在构建我们的模型时,我们假设它表现出随机过程,是平稳的,并且遵循高斯分布。随机过程是指描述系统或现象随时间演变的数学模型,其结果具有不确定性或随机性。在随机过程的背景下,平稳性意味着过程的统计特性随着时间的推移保持不变。具体来说,这意味着过程的均值、方差和自协方差不随时间或时间原点的变化而变化。

平稳性原理。来源
我们拥有一个数组f,表示其所有元素的黑盒函数的值。我们假设这个数组服从正态分布。

概率密度函数将采用高斯密度函数的形式。
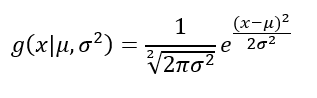
由于我们假设平稳性,因此联合概率分布随时间保持恒定,这意味着它是时不变的。函数的平均值是m。协方差预计呈现高斯形状,并且可以使用径向基函数 (RBF) 核进行近似。
接下来,我们需要一个预测函数,旨在根据我们手头的可用数据估计函数f (x)的概率。

具有 0 均值和 ~C 协方差的正态分布优于具有 0 均值和 C 协方差的正态分布。
现在,我们可以简化它。

k是 RBF 核的数组。C 是协方差矩阵。

使用此预测函数,我们可以推断,平均而言,未知函数将在 x 处取值 μ,并伴有方差 σ。
因此,代理函数的算法或多或少是:
- 迭代我们希望执行评估的输入 x 的每个样本值。
- 使用 RBF 内核构建k和f向量。
- 构建矩阵C和C~。
- 计算μ和σ。
- 将μ附加到预测的Mu 数组,将 σ附加到预测的 Sigma数组。
2. 计算Omega作为采样点的黑盒函数的平均值。
3.计算Kappa=预测Mu+Omega
4、退货:
- Kappa,替代函数的平均估计
- PredictedSigma,代理函数的方差估计。
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
# Gaussian process regressor with an RBF kernel
kernel = RBF(length_scale=1.0)
gp_model = GaussianProcessRegressor(kernel=kernel)
# Fit the Gaussian process model to the sampled points
gp_model.fit(sample_x.reshape(-1, 1), sample_y)
# Generate predictions using the Gaussian process model
y_pred, y_std = gp_model.predict(x_range.reshape(-1, 1), return_std=True)
# Plot
plt.figure(figsize=(10, 6))
plt.plot(x_range, black_box_function(x_range), label='Black Box Function')
plt.scatter(sample_x, sample_y, color='red', label='Samples')
plt.plot(x_range, y_pred, color='blue', label='Gaussian Process')
plt.fill_between(x_range, y_pred - 2*y_std, y_pred + 2*y_std, color='blue', alpha=0.2)
plt.xlabel('x')
plt.ylabel('Black Box Output')
plt.title('Black Box Function with Gaussian Process Surrogate Model')
plt.legend()
plt.show()
高斯过程图。图片由作者提供。
八、采集功能
我们如何选择代理函数的下一个点?
采集函数确定要在搜索空间中评估的下一个点或一组点。它根据优化过程的当前状态量化对特定点进行采样的潜在效用或可取性。获取函数的目的是平衡探索和开发。
它考虑了替代模型的预测值以及与这些预测相关的不确定性。它结合了这两个方面来识别预计具有高目标函数值和(或)高不确定性的点,表明有改进的潜力。
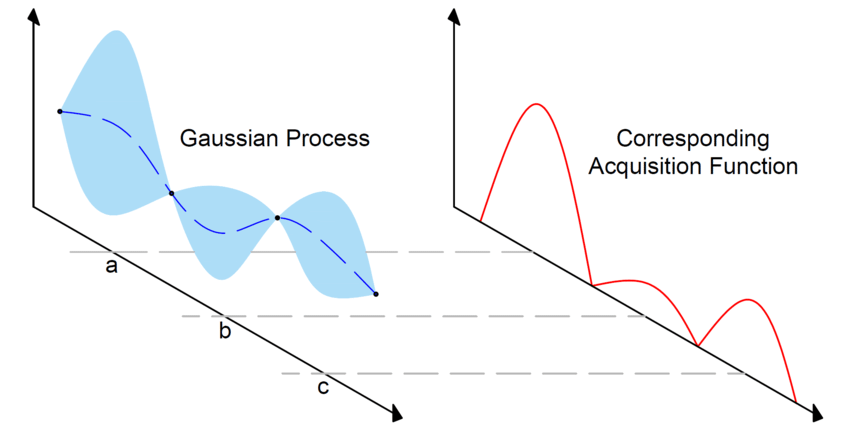
用于选择下一个评估点的获取函数。来源
贝叶斯优化中使用了几种采集函数:
- 预期改进 (EI) 选择有可能改进最佳观察值的点。它量化了相对于当前最佳值的预期改进,并考虑了替代模型的平均预测及其不确定性。
from scipy.stats import norm
def expected_improvement(x, gp_model, best_y):
y_pred, y_std = gp_model.predict(x.reshape(-1, 1), return_std=True)
z = (y_pred - best_y) / y_std
ei = (y_pred - best_y) * norm.cdf(z) + y_std * norm.pdf(z)
return ei
# Determine the point with the highest observed function value
best_idx = np.argmax(sample_y)
best_x = sample_x[best_idx]
best_y = sample_y[best_idx]
ei = expected_improvement(x_range, gp_model, best_y)
# Plot the expected improvement
plt.figure(figsize=(10, 6))
plt.plot(x_range, ei, color='green', label='Expected Improvement')
plt.xlabel('x')
plt.ylabel('Expected Improvement')
plt.title('Expected Improvement')
plt.legend()
plt.show()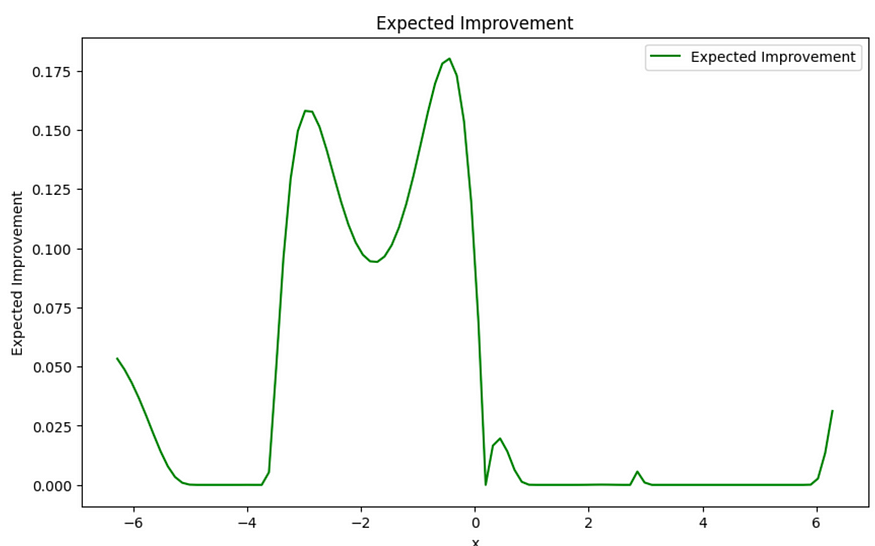
预期改善。图片由作者提供。
- 置信上限 (UCB) 通过平衡替代模型的平均预测和与不确定性成比例的探索项来权衡探索和利用。它选择在预测高值和探索不确定区域之间提供良好平衡的点。
def upper_confidence_bound(x, gp_model, beta):
y_pred, y_std = gp_model.predict(x.reshape(-1, 1), return_std=True)
ucb = y_pred + beta * y_std
return ucb
beta = 2.0
# UCB
ucb = upper_confidence_bound(x_range, gp_model, beta)
plt.figure(figsize=(10, 6))
plt.plot(x_range, ucb, color='green', label='UCB')
plt.xlabel('x')
plt.ylabel('UCB')
plt.title('UCB')
plt.legend()
plt.show()
UCB。图片由作者提供。
- 改进概率 (PI) 估计某个点在当前最佳值基础上改进的概率。它考虑平均预测与当前最佳值之间的差异,并考虑替代模型中的不确定性。
def probability_of_improvement(x, gp_model, best_y):
y_pred, y_std = gp_model.predict(x.reshape(-1, 1), return_std=True)
z = (y_pred - best_y) / y_std
pi = norm.cdf(z)
return pi
# Probability of Improvement
pi = probability_of_improvement(x_range, gp_model, best_y)
plt.figure(figsize=(10, 6))
plt.plot(x_range, pi, color='green', label='PI')
plt.xlabel('x')
plt.ylabel('PI')
plt.title('PI')
plt.legend()
plt.show()
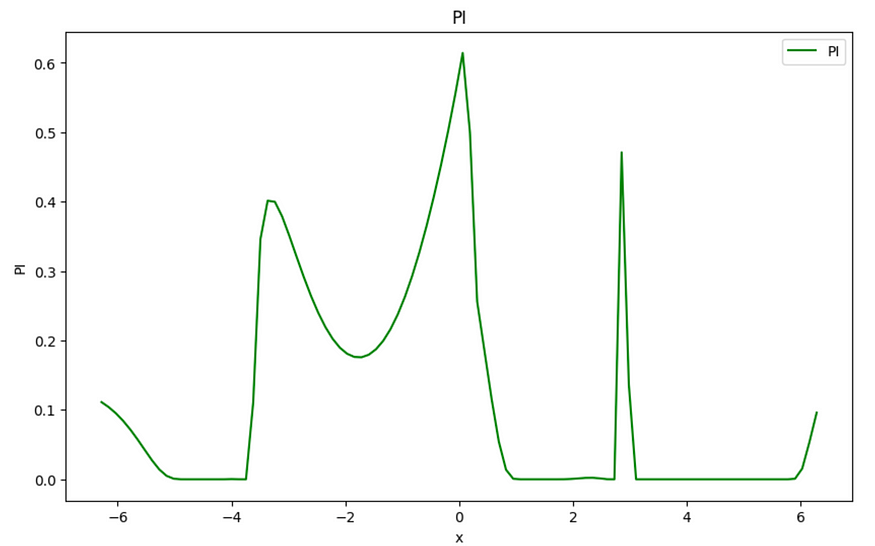
PI。图片由作者提供。
无论使用哪种方法,我们都会选择 y 轴上具有最高值的点。
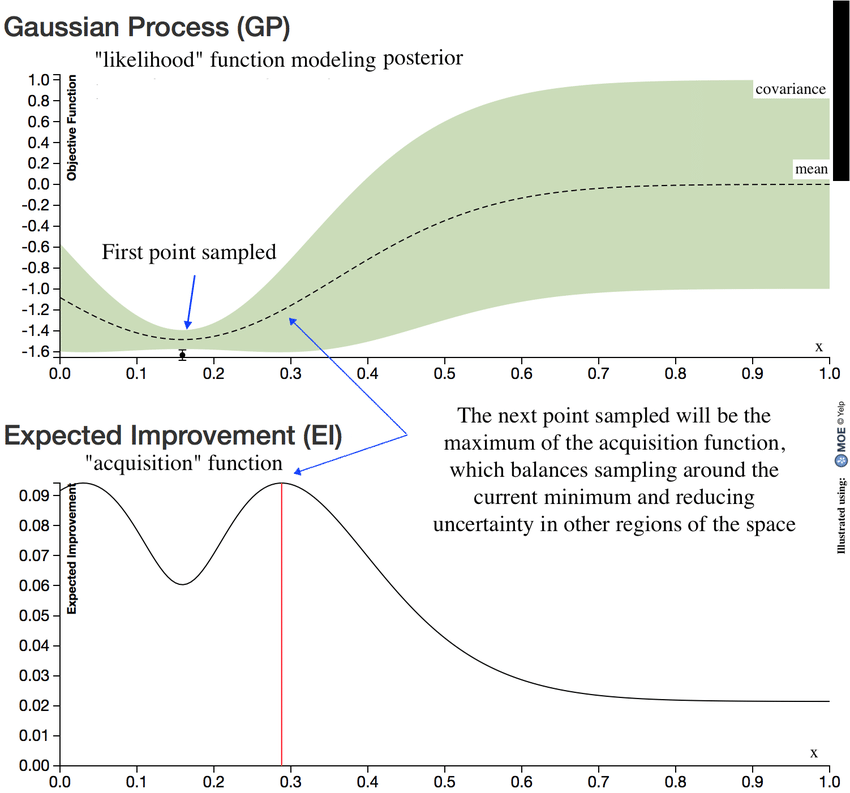
贝叶斯优化中的后验函数和采集函数。来源
num_iterations = 5
plt.figure(figsize=(10, 6))
for i in range(num_iterations):
# Fit the Gaussian process model to the sampled points
gp_model.fit(sample_x.reshape(-1, 1), sample_y)
# Determine the point with the highest observed function value
best_idx = np.argmax(sample_y)
best_x = sample_x[best_idx]
best_y = sample_y[best_idx]
# Set the value of beta for the UCB acquisition function
beta = 2.0
# Generate the Upper Confidence Bound (UCB) using the Gaussian process model
ucb = upper_confidence_bound(x_range, gp_model, beta)
# Plot the black box function, surrogate function, previous points, and new points
plt.plot(x_range, black_box_function(x_range), color='black', label='Black Box Function')
plt.plot(x_range, ucb, color='red', linestyle='dashed', label='Surrogate Function')
plt.scatter(sample_x, sample_y, color='blue', label='Previous Points')
if i < num_iterations - 1:
new_x = x_range[np.argmax(ucb)] # Select the next point based on UCB
new_y = black_box_function(new_x)
sample_x = np.append(sample_x, new_x)
sample_y = np.append(sample_y, new_y)
plt.scatter(new_x, new_y, color='green', label='New Points')
plt.xlabel('x')
plt.ylabel('y')
plt.title(f"Iteration #{i+1}")
plt.legend()
plt.show()
迭代#1。图片由作者提供。

迭代#2。图片由作者提供。

迭代#3。图片由作者提供。

迭代#4。图片由作者提供。
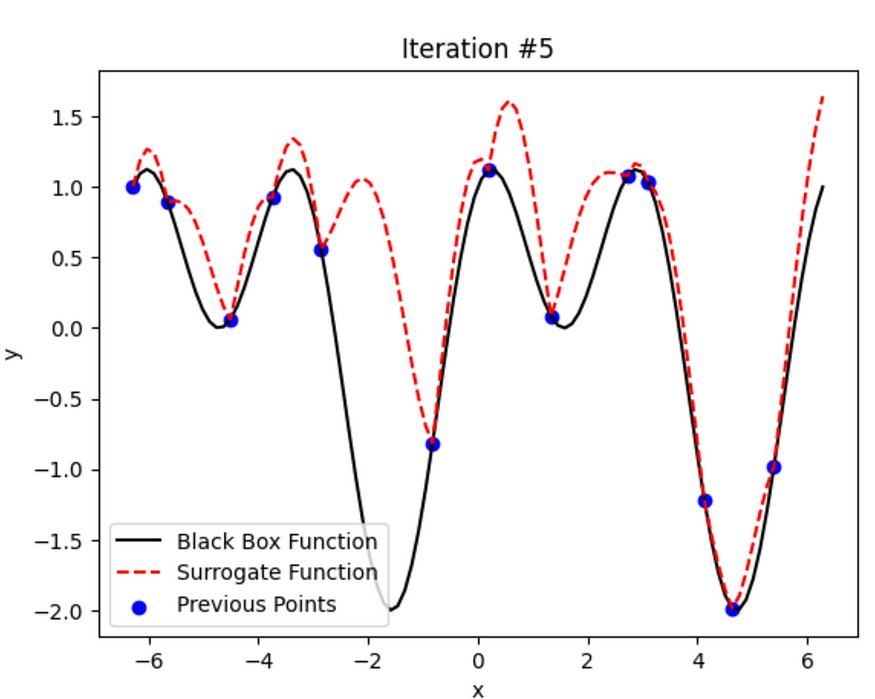
迭代#5。图片由作者提供。
很酷,对吧?它在每次迭代中不断学习和改进。
贝叶斯优化提供了几个积极的方面。其主要优点之一是能够优化缺乏分析梯度或具有噪声评估的黑盒函数。采用代理模型(例如高斯过程)可以平衡探索和利用,以有效地搜索最佳解决方案。它提供了一种迭代选择点的原则方法,可以在探索未探索的区域和开发有前途的区域之间提供良好的权衡。
它在各个领域都有应用。它特别适合机器学习中的超参数调整。它可用于优化复杂的模拟、实验设计以及目标函数评估成本高昂或耗时的其他场景。